I was simply explaining why the plots were different.
As for getting y as functions, respectively, of Re[x] and Im[x], that gets tricky because it is in general not a function but rather a "multivalued function". You will probably want to get a continuous branch of such inverses. One method you might consider is to find a value for y at a given re(x), say, and then trace from there by setting up an NDSolve equation.
Lets define the real and imaginary parts of f as ref and imf respectively. And the real and imaginary parts of x we will call rex and imx. The equations you have are {ref[rex,imx,y]==0,imf[rex,imx,y]==0}. To inverst y in terms of rex, treat it as a function of rex (the whole point of the exercise) and differentiate. I'll show explicit code for your example.
expr = y*Sqrt[(y^2 + 1/10*I*y - 4)/(2 y^2 + 1/10*2*I*y - 4)];
sys = {rex, imx} - ComplexExpand[{Re[expr], Im[expr]},TargetFunctions -> {Re, Im}];
dsys = D[sys /. {y -> y[rex], imx -> imx[rex]}, rex];
yinit = .1;
init = expr /. y -> yinit;
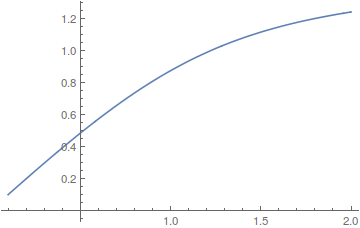
soly = NDSolveValue[Flatten[{Thread[dsys == 0], y[Re[init]] == yinit,
imx[Re[init]] == Im[init]}], y[rex], {rex, Re[init], 2}]
(* Out[77]= InterpolatingFunction[{{0.100125, 2.}}, <>][rex] *)
Plot[soly, {rex, Re[init], 2}]