Thank you. But can I further extract two 2D graphs from this 3D graph? I mean I can plot F[Re[x],Im[x],y]=0, but I would like to get two projections of this graph: Re[x],y and Im[x],y.

Dear Daniel, thank you so much for your help! Hovewer, I am not sure that this is exactly what I need, because I don't quietly understand how it works.

I can explain what I need in other words. I need the graph of the equation F[x,y]=0, x is a complex number, y is a real number, {y,0,8}. The graph of this equation is 3D, because we have 3 variables Re[x], Im[x], y. I need two 2D graphs y as a function of Re[x] and Im[x], I mean that I need two projection of this 3D graph.

Dear Daniel, could you clarify how do you do this? I try to use your code, but I don't get a result.g = 1/10; expr = x - Sqrt[y^2 + I*y]; e2 = expr /. x -> s + I*t; {re, im} = ComplexExpand[{Re[e2], Im[e2]}]; root[yval_?NumericQ] := {s, t} /. FindRoot[{re == 0, im == 0} /. y -> yval, {s, RandomReal[{-5, 5}]}, {t, RandomReal[{-5, 5}]}] pts = Quiet[Table[root[j], {j, .01, 8, .01}]]; ListPlot[pts]

Attachments:

Dear Daniel, I am sorry for interruption. I don't know what was the problem, but now everything is fine. Could you answer a couple of other questions? Firstly, what shoul I do to consider this problem only in the region {Im[x],0,8}, {Re[x],0,8}, {y,0,8}. And how can I distinguish between the dependense of y on Re[x] and y on Im[x] depicted on the figure? Also, could you clarify what do I change when alter RandomReal[{0, 5}] and {j, .01, 5, .01}?

Attachments:

I was simply explaining why the plots were different.

As for getting y as functions, respectively, of Re[x] and Im[x], that gets tricky because it is in general not a function but rather a "multivalued function". You will probably want to get a continuous branch of such inverses. One method you might consider is to find a value for y at a given re(x), say, and then trace from there by setting up an NDSolve equation.

Lets define the real and imaginary parts of f as ref and imf respectively. And the real and imaginary parts of x we will call rex and imx. The equations you have are {ref[rex,imx,y]==0,imf[rex,imx,y]==0}. To inverst y in terms of rex, treat it as a function of rex (the whole point of the exercise) and differentiate. I'll show explicit code for your example.

expr = y*Sqrt[(y^2 + 1/10*I*y - 4)/(2 y^2 + 1/10*2*I*y - 4)];
sys = {rex, imx} - ComplexExpand[{Re[expr], Im[expr]},TargetFunctions -> {Re, Im}];
dsys = D[sys /. {y -> y[rex], imx -> imx[rex]}, rex];
yinit = .1;
init = expr /. y -> yinit;

soly = NDSolveValue[Flatten[{Thread[dsys == 0], y[Re[init]] == yinit, 
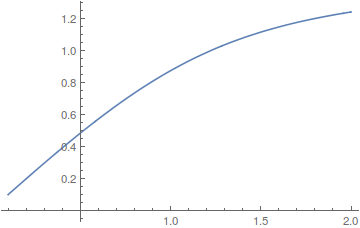
    imx[Re[init]] == Im[init]}], y[rex], {rex, Re[init], 2}]

(* Out[77]= InterpolatingFunction[{{0.100125, 2.}}, <>][rex] *)

Plot[soly, {rex, Re[init], 2}]

I'm using version 10.1. You can do similarly with NDSolve if you solve for both {y[rex],imx[rex]}.

Dear Daniel, I have installed Mathematica 10, but again I can't use your code.

Attachments:

This might be a start. Define the expression, then use ComplexExpand to form explicit real and imaginary parts.

g = 1/10;
expr = 
  Tanh[Sqrt[-x^2 - y^2]*3/10] (y^2 + I*g*y - 4) Sqrt[-x^2 - 
      y^2] + (y^2 + I*g*y) Sqrt[-x^2 - 
      y^2 ((y^2 + I*g*y - 4)/(y^2 + I*g*y))];

e2 = expr /. x -> s + I*t;
{re, im} = ComplexExpand[{Re[e2], Im[e2]}];

 ContourPlot[(re /. y -> 0.7) == 0, {s, -10, 10}, {t, -10, 10}]

ContourPlot[(im /. y -> 0.7) == 0, {s, -10, 10}, {t, -10, 10}]

You will get better answers if you give a complete, very specific example of what you want.