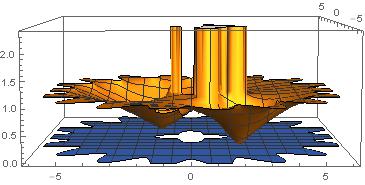
In my previous reply, i got the figure 1 from following codes (ffNoin is my function from my theory)
Gro[zz_] := ffNoin[zz]
Grp[x_, y_] := Gro[x + I y]
Plot3D[{Abs[Grp[x, y]], 0}, {x, -6, 6}, {y, -6, 6},
RegionFunction ->
Function[{x, y, z},
1.2 + 0.4 Cos[4 ArcTan[x, y]] < Sqrt[x^2 + y^2] <
6 + 0.8 Cos[18 ArcTan[x, y]]]]
 But if i also include z<=1, the i get the following
But if i also include z<=1, the i get the following
Gro[zz_] := ffNoin[zz]
Grp[x_, y_] := Gro[x + I y]
Plot3D[{Abs[Grp[x, y]], 0}, {x, -6, 6}, {y, -6, 6},
RegionFunction ->
Function[{x, y, z},
1.2 + 0.4 Cos[4 ArcTan[x, y]] < Sqrt[x^2 + y^2] <
6 + 0.8 Cos[18 ArcTan[x, y]], z <= 1]]
Attributes::attnf: z<=1 is not a known attribute. >>
Attributes::attnf: z<=1 is not a known attribute. >>
Plot3D::invregion: Function[{x,y,z},1.2 +0.4 Cos[4 ArcTan[x,y]]<Sqrt[x^2+y^2]<6+0.8 Cos[18 ArcTan[x,y]],z<=1] must be a Boolean function. >>
Plot3D::invregion: Function[{x,y,z},1.2 +0.4 Cos[4 ArcTan[x,y]]<Sqrt[x^2+y^2]<6+0.8 Cos[18 ArcTan[x,y]],z<=1] must be a Boolean function. >>
Attributes::attnf: z<=1 is not a known attribute. >>
General::stop: Further output of Attributes::attnf will be suppressed during this calculation. >>
Plot3D::invregion: Function[{x,y,z},1.2 +0.4 Cos[4 ArcTan[x,y]]<Sqrt[x^2+y^2]<6+0.8 Cos[18 ArcTan[x,y]],z<=1] must be a Boolean function. >>
General::stop: Further output of Plot3D::invregion will be suppressed during this calculation. >>
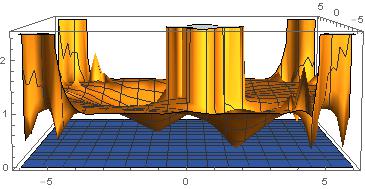
I need the bottom portion (in plane) same like in first figure and 3D portion to merge in the unit circle.