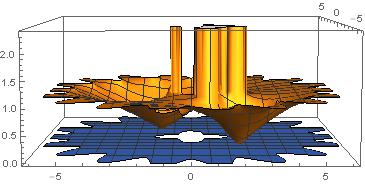
In my previous reply, i got the figure 1 from following codes (ffNoin is my function from my theory)

Gro[zz_] := ffNoin[zz]
Grp[x_, y_] := Gro[x + I y]
Plot3D[{Abs[Grp[x, y]], 0}, {x, -6, 6}, {y, -6, 6}, 
 RegionFunction -> 
  Function[{x, y, z}, 
   1.2 + 0.4 Cos[4 ArcTan[x, y]] < Sqrt[x^2 + y^2] < 
    6 + 0.8 Cos[18 ArcTan[x, y]]]]

But if i also include z<=1, the i get the following

Gro[zz_] := ffNoin[zz]
Grp[x_, y_] := Gro[x + I y]
Plot3D[{Abs[Grp[x, y]], 0}, {x, -6, 6}, {y, -6, 6}, 
 RegionFunction -> 
  Function[{x, y, z}, 
   1.2 + 0.4 Cos[4 ArcTan[x, y]] < Sqrt[x^2 + y^2] < 
    6 + 0.8 Cos[18 ArcTan[x, y]], z <= 1]]

Attributes::attnf: z<=1 is not a known attribute. >>

Attributes::attnf: z<=1 is not a known attribute. >>

Plot3D::invregion: Function[{x,y,z},1.2 +0.4 Cos[4 ArcTan[x,y]]<Sqrt[x^2+y^2]<6+0.8 Cos[18 ArcTan[x,y]],z<=1] must be a Boolean function. >>

Plot3D::invregion: Function[{x,y,z},1.2 +0.4 Cos[4 ArcTan[x,y]]<Sqrt[x^2+y^2]<6+0.8 Cos[18 ArcTan[x,y]],z<=1] must be a Boolean function. >>

Attributes::attnf: z<=1 is not a known attribute. >>

General::stop: Further output of Attributes::attnf will be suppressed during this calculation. >>

Plot3D::invregion: Function[{x,y,z},1.2 +0.4 Cos[4 ArcTan[x,y]]<Sqrt[x^2+y^2]<6+0.8 Cos[18 ArcTan[x,y]],z<=1] must be a Boolean function. >>

General::stop: Further output of Plot3D::invregion will be suppressed during this calculation. >>

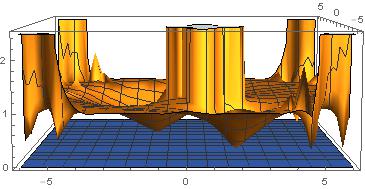
I need the bottom portion (in plane) same like in first figure and 3D portion to merge in the unit circle.

Helllo , I am really thankful to all members who responded my problem, and these suggestions really helped me and i have now the following 3D graph, I want to merge 3D graph in (figure1) below into unit circle ( as like in figure 2) but on plane i need the same curve as in the following first figure

Figure1
Figure2

And if you need a 3D shape you can proceed also as follows: Convert to cartesian using FromPolarCoordinates:

In[18]:= gear[\[Theta]_] := {1 + 
   1/8 Sin[18 (\[Theta] - \[Pi]/4)], \[Theta]}
FromPolarCoordinates[gear[\[Theta]]]
ParametricPlot[%, {\[Theta], 0, 2 \[Pi]}]

Out[19]= {Cos[\[Theta]] (1 + 1/8 Sin[18 (-(\[Pi]/4) + \[Theta])]), 
 Sin[\[Theta]] (1 + 1/8 Sin[18 (-(\[Pi]/4) + \[Theta])])}

Insert a 3rd dimension (eg in the y direction) and make a ParametricPlot3D:

In[30]:= Insert[FromPolarCoordinates[gear[\[Theta]]], y, 2]
ParametricPlot3D[%, {\[Theta], 0, 2 \[Pi]}, {y, 0, 1}, 
 PlotPoints -> 25, PlotTheme -> "Marketing",  
 PerformanceGoal -> "Quality"]

Out[30]= {Cos[\[Theta]] (1 + 1/8 Sin[18 (-(\[Pi]/4) + \[Theta])]), y, 
 Sin[\[Theta]] (1 + 1/8 Sin[18 (-(\[Pi]/4) + \[Theta])])}

I presume the polar equation of yr plot is:

r->1 + 1/8 Sin[18 \[Theta]
PolarPlot[(1 + 1/8 Sin[18 \[Theta]]), {\[Theta], 0, 2 \[Pi]}]

If you convert to Cartesian, you get ann intrinsic equation of the gear shape:

1 + 1/8 Sin[18 ArcTan[x, y]] == Sqrt[x^2 + y^2]
ContourPlot[
 1 + 1/8 Sin[18 ArcTan[x, y]] == Sqrt[x^2 + y^2], {x, -1.15, 
  1.15}, {y, -1.15, 1.15}, Axes -> True]

Can this be any help?: Plotting Extruded Profiles