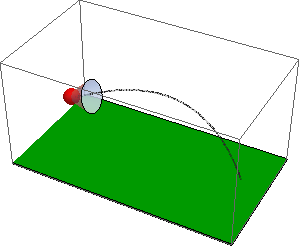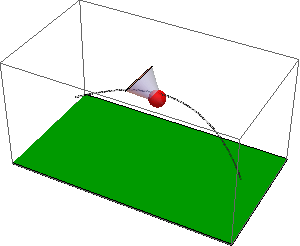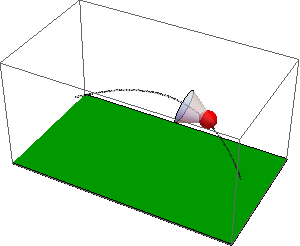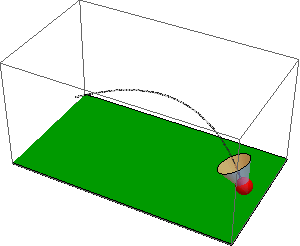
See attached notebook for details. A shuttlecock (previously called Shuttlecork) (also called a bird or birdie) is a high-drag projectile used in the sport of badminton. It has an open conical shape: the cone is formed from 16 or so overlapping feathers, usually goose or duck, embedded into a rounded cork base. The cork is covered with thin leather. The shuttlecock's shape makes it extremely aerodynamically stable. Regardless of initial orientation, it will turn to fly cork first, and remain in the cork-first orientation.
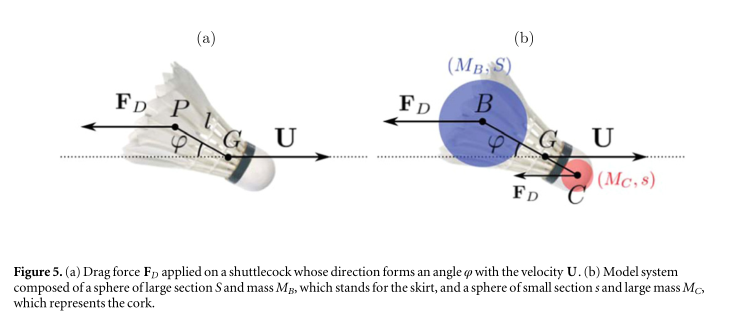
Image courtesy of IOP Science
The name shuttlecock is frequently shortened to shuttle. The "shuttle" part of the name was probably derived from its back-and-forth motion during the game, resembling the shuttle of a loom; the "cock" part of the name was probably derived from the resemblance of the feathers to those on a cockerel.

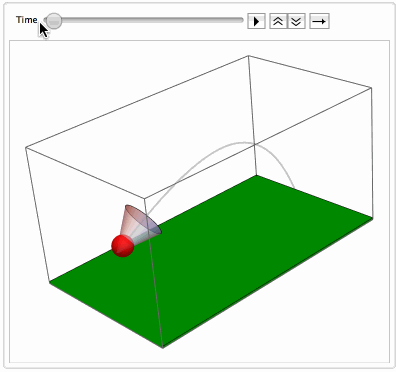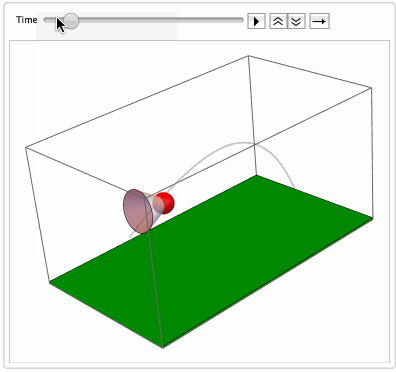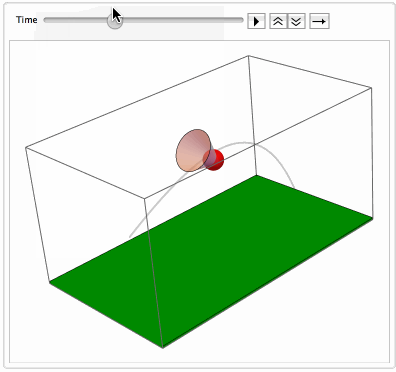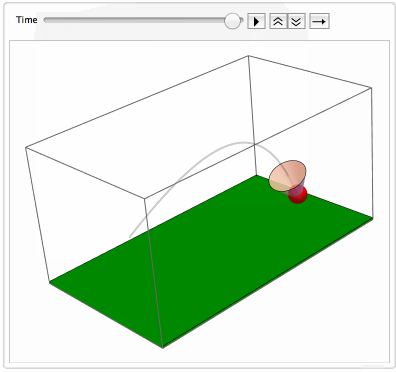
The code with NDSolveValue is attached. Here is the resulting simulation of the flight of badminton shuttlecocks:
References
 Attachments:
Attachments: