Message Boards Message Boards

Coding new pentagon tiling

Ed Pegg, Wolfram Research
Posted 10 years ago

On 29 July, I saw a tweet that a 15th type of tiling pentagon had been discovered by Casey Mann, Jennifer McLoud-Mann, and David Von Derau at the University of Washington, Bothell. I immediately added it to my Pentagon Tilings Demonstration, then went over to Wikipedia's pentagonal tiling page to update my 2009 image made from the demo. A week later image was widely published in such places as The Guardian and npr.org.

pentagon tilings

The pentagon tiles with a motif of 12 pentagons.

pent15 ={
{{-17-6 s,2-s},{-17-6 s,6-s},{-13-6 s,3 (2+s)},{-11-6 s,6+s},{-13-6 s,2-s}},  
{{-13-4 s,-s},{-11-4 s,s},{-11-4 s,8+s},{-11-6 s,6+s},{-13-6 s,2-s}},  
{{-11-6 s,6+s},{-11-4 s,8+s},{-7-4 s,8+5 s},{-11-4 s,8+5 s},{-13-6 s,3 (2+s)}},  
{{-13-4 s,-s},{-13-2 s,-2-s},{-5-2 s,-2-s},{-7-2 s,-2+s},{-11-4 s,s}},  
{{-11-4 s,4+s},{-7-4 s,4+s},{-7,s},{-7-2 s,-2+s},{-11-4 s,s}},  
{{-7-2 s,-2+s},{-7,s},{1,s},{-1,-s},{-5-2 s,-2-s}},  
{{17+6 s,-2+s},{17+6 s,-6+s},{13+6 s,-3 (2+s)},{11+6 s,-6-s},{13+6 s,-2+s}},  
{{13+4 s,s},{11+4 s,-s},{11+4 s,-8-s},{11+6 s,-6-s},{13+6 s,-2+s}},  
{{11+6 s,-6-s},{11+4 s,-8-s},{7+4 s,-8-5 s},{11+4 s,-8-5 s},{13+6 s,-3 (2+s)}},  
{{13+4 s,s},{13+2 s,2+s},{5+2 s,2+s},{7+2 s,2-s},{11+4 s,-s}},  
{{11+4 s,-4-s},{7+4 s,-4-s},{7,-s},{7+2 s,2-s},{11+4 s,-s}},  
{{7+2 s,2-s},{7,-s},{-1,-s},{1,s},{5+2 s,2+s}}}/8/.s->Sqrt[3];  

offset15 = {{9 + 4 Sqrt[3], -8 - 5 Sqrt[3]}/4, {3 + Sqrt[3], 1 + Sqrt[3]}/4};

Here's some code to display it. 

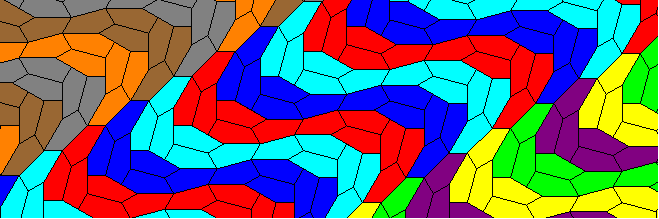
motif = Polygon /@ pent15;
colors = {{Red, Blue, Cyan}, {Yellow, Green, Purple}, {Orange, Brown, Gray}};
Graphics[{EdgeForm[Black], Table[{colors[[Mod[x, 3, 1], Mod[y, 3, 1]]], Translate[motif, x offset15[[1]] + y offset15[[2]]]}, 
{x, 0, 2}, {y, -5, 8}]}, PlotRange -> {{-3, 15}, {-6, 0}}, ImageSize -> {660, 220}]

The fifteenth pentagon

With all the interest in pentagons, I figured I should make a Demonstration for tetratoid pentagons, where twelve irregular pentagons can make a polyhedron. But I haven't found the intersection between tetratoid pentagons and tiling pentagons.

What sort of image can you make from these or other pentagons?
POSTED BY: Ed Pegg
3 Replies
Sort By:

The Demonstration Ed mentioned for Tetartoid is very interesting. It driven by a multiset {a,b,c} has quite a few "degenerate" states for multiset like {n, m, n} when polyhedron collapses into a cube or pyramid. See this animation:

enter image description here

The new pentagonal tiling is striking. I'd like to note that is was found by using a computer algorithm (I wonder which):

We discovered the tile using a computer to exhaustively search through a large but finite set of possibilities,” ~ Casey Mann.

Here is a bit changed Ed's code to see how it is formed via translations of main motif ( do you have any other related visualizations ? - please share! ):

motif = Polygon[pent15];
Rotate[Graphics[{EdgeForm[Directive[Black, Opacity[.3]]], Table[{RandomColor[], 
Translate[motif, x offset15[[1]] + y offset15[[2]]]}, {x, 0, 2}, {y, 0, 8}]}], .85]

enter image description here
POSTED BY: Vitaliy Kaurov
Ed Pegg
Ed Pegg, Wolfram Research
Posted 10 years ago

I decided to simplify and compress the motif. The offset got simplified to {{3 (1 + Sqrt[3])/2, 0}, {0, 1}} in the process.

p15 = {
{{5-5 s,1+s},{5-5 s,5-3 s},{1-s,-7+s},{-1+s,-1-s},{1-s,1+s}},
{{-5-3 s,7-s},{-7-s,1+s},{5-5 s,5-3 s},{5-5 s,1+s},{1-5 s,5+s}},
{{-1-3 s,11-s},{5-5 s,13-3 s},{1-s,1+s},{5-5 s,1+s},{1-5 s,5+s}},
{{-1-3 s,3-s},{1-5 s,-3+s},{-11-s,1-3 s},{-11-s,-3+s},{-7-s,1+s}},
{{-5-3 s,7-s},{-11-s,9-3 s},{-7-5 s,-3+s},{-11-s,-3+s},{-7-s,1+s}},
{{-11-s,-3+s},{-11-s,1-3 s},{-7-5 s,-11+s},{-5-7 s,-5-s},{-7-5 s,-3+s}}}/8/.s->Sqrt[3];

This allows a more compact presentation.

motif = Polygon /@ Join[p15, -p15];
colors = {{Red, Blue, Brown}, {Yellow, Orange, Purple}, {Green, Cyan, White}};
Graphics[{EdgeForm[Black], Table[{colors[[Mod[x, 3, 1], Mod[y, 3, 1]]], 
Translate[motif, {x 3 (1 + Sqrt[3])/2, y }]}, {x, -1, 1}, {y, -3, 3}]},
 PlotRange -> {{-4.5, 4.5}, {-1.5, 1.5}}, ImageSize -> {660, 220}]

the 15th tiling pentagon
POSTED BY: Ed Pegg

enter image description here -- you have earned Featured Contributor Badge enter image description here Your exceptional post has been selected for our editorial column Staff Picks http://wolfr.am/StaffPicks and Your Profile is now distinguished by a Featured Contributor Badge and is displayed on the Featured Contributor Board. Thank you!
POSTED BY: EDITORIAL BOARD
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract