Start with 4. Progressively add or subtract the integers, repeating the sequence + + - - + + -.
FoldList[Plus,4,Flatten[Table[{1,1,-1,-1,1,1,-1}, {20}]] Range[140]]
4, 5, 7, 4, 0, 5, 11, 4, 12, 21, 11, 0, 12, 25, 11, 26, 42, 25, 7, 26, 46, 25, 47, 70, 46, 21, 47, 74, 46, 75, 105, 74, 42, 75, 109, 74, 110, 147, 109, 70, 110, 151, 109, 152, 196, 151, 105, 152, 200, 151, 201, 252, 200, 147, 201, 256, 200, 257, 315, 256, 196, 257, 319, 256, 320, 385, 319, 252, 320, 389, 319, 390, 462, 389, 315, 390, 466, 389, 467, 546, 466, 385, 467, 550, 466, 551, 637, 550, 462, 551, 641, 550, 642, 735, 641, 546, 642, 739, 641, 740, 840, 739, 637, 740, 844, 739, 845, 952, 844, 735, 845, 956, 844, 957, 1071, 956, 840, 957, 1075, 956, 1076, 1197, 1075, 952, 1076, 1201, 1075, 1202, 1330, 1201, 1071, 1202, 1334, 1201, 1335, 1470, 1334, 1197, 1335, 1474, 1334
The differences are 1, 2, -3, -4, 5, 6, -7, .... 8, 9, -10, -11, 12, 13, -14, .... 15, 16, -17, -18, 19, 20, -21, and so on. UUDDUUD.
Notice how all the numbers in the sequence repeat themselves two or three times.
Only 3/7th of the integers appear this sequence, namely 7 times the triangular numbers plus (0,4,5) or (5,4,0). The numbers can be placed in a grid as follows.
Grid[Transpose[Table[7 n (n - 1)/2 + If[OddQ[n], {0, 4, 5}, {5, 4, 0}], {n, 1, 10}]]]
0 . 12 . 21 . 47 . 70 . 110 . 147 . 201 . 252 . 320
4 . 11 . 25 . 46 . 74 . 109 . 151 . 200 . 256 . 319
5 . 07 . 26 . 42 . 75 . 105 . 152 . 196 . 257 . 315
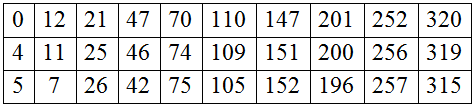
Try it yourself -- start with 4, 5, 7, 4, 0, 5 -- that last move wouldn't be a king move, but from then on all moves are king moves. From the 5, find a move that will increase or decrease 6, then increase or decrease 7, then increase or decrease 8, ...