Dear Todd,
thank you very much for your encouraging words.
About the data relevant to the MH370 flight, do you know if the data
from 2014 is available? Or is there a way for you to post some small
amount of data like average currents for the Indian ocean?
There is indeed some more data available on the website. If you go to this page, which I used for the download, you will see that there is data available for up to the end of October 2014.
You seen that the last file name ends in 20140124.nc, which indicates the date.That end data is, of course, not quite enough to follow the debris of the plane through the ocean, but you can use is for the first couple of months and then use the older data from previous years and make a sort of ensemble prediction over the flow in different years.
This is also what could be done in case of an oilspill, where flow data for predictions is not readily available. It is also interesting to study how different the paths of the particles are if you study at different times, i.e. current conditions.
Another interesting thing to try might be to use the data for different depths. If you open a file the top of it looks like this:
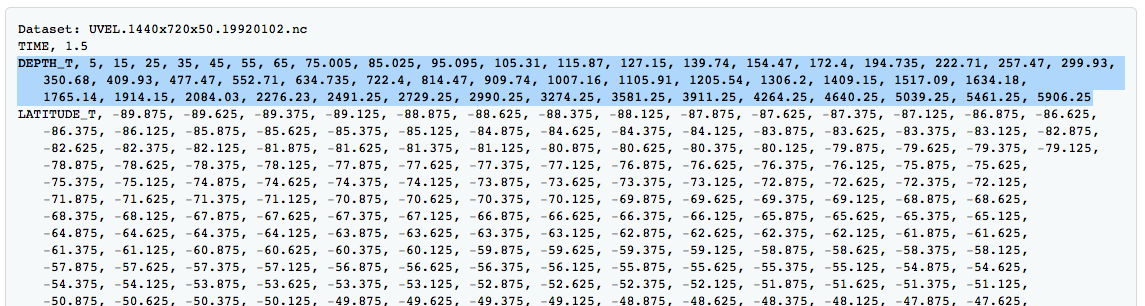
so we get all sorts of data for various different depths, not only the surface. This could be quite valuable for applications.
There are lots of other things to try. Here I have a gif-animation of the particle movements for the Fukushima scenario:
Export["~/Desktop/swarm.gif",
Table[Graphics[{RGBColor[i/1238., 1. - i/1238., 0.], Opacity[0.8],
Disk[#, 3]} & /@ trajectories[[i, 1 ;; 1000, {3, 2}]],
PlotRange -> {{470, 950}, {380, 570}}, ImageSize -> Full,
Background -> Black], {i, 1, 1236, 5}]]

You can use Image3D to get a representation of it, which can (after slight modification) be 3D printed.
Image3D[Import["~/Desktop/swarm.gif"]]

The "green top" shows the earlier times, and the "red bottom" the later ones.
Thanks a lot for your comments; I really appreciate it.
Cheers,
Marco
BTW, you can get pretty nice effects with ContourPlot:
ListContourPlot[veltottot, AspectRatio -> 1/2, ImageSize -> Full, ColorFunction -> "TemperatureMap", Frame -> None, Contours -> 7]
