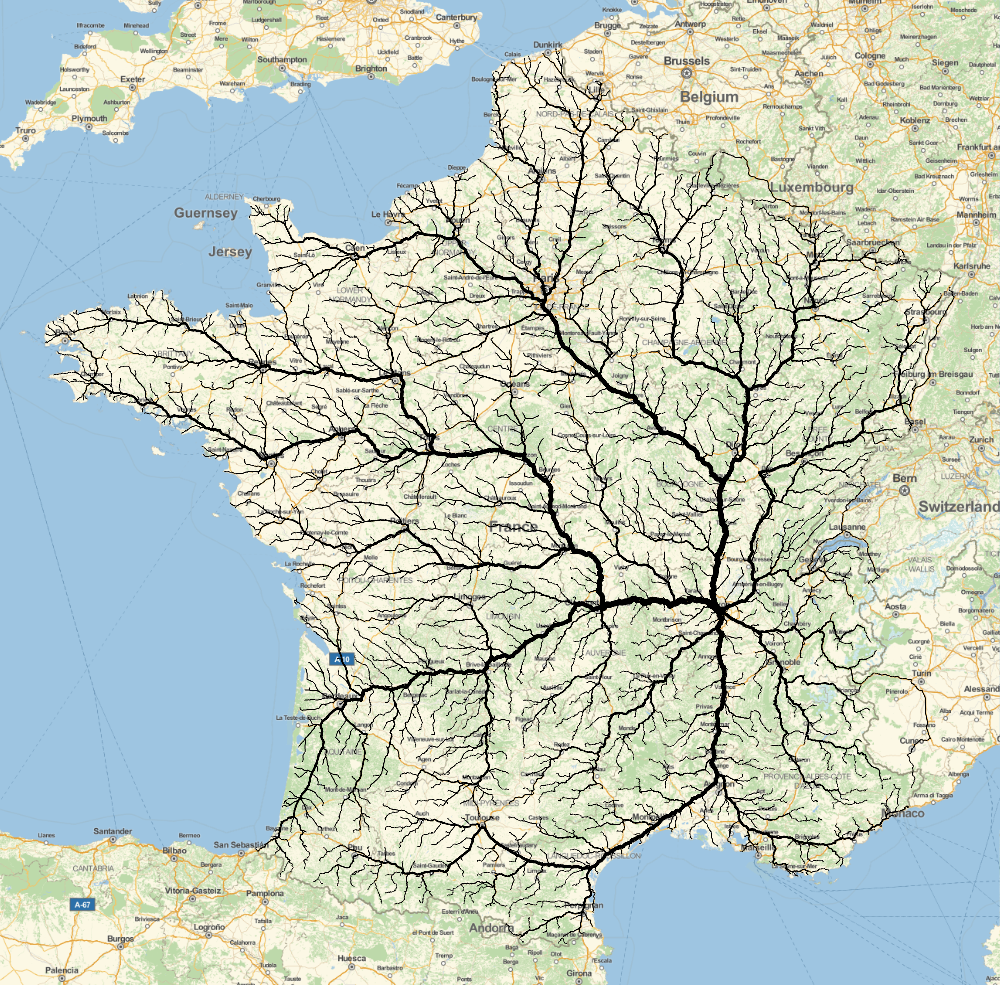
I was inspired by the Roads to Rome post (here). And wanted to check what it would look like to the town I'm living in now (Lyon, France). Here is the result and the method and code are below:
We first make a database of coordinates of cities in France:
SetDirectory[NotebookDirectory[]];
cities = CityData[{All, "France"}];
citiesloc = CityData[#, "Coordinates"] & /@ cities;
citiesloc = DeleteMissing[citiesloc, 1, \[Infinity]];
Export["francecities.txt", citiesloc, "Table"]
quite self-explanatory, it will save it as a table of coordinates.
Now I read those back in, and check find those that are in 'mainland' France and create a nearest-function of those coordinates:
SetDirectory[NotebookDirectory[]];
citiesloc = Import["francecities.txt", "Table"];
reg = CountryData["France", "Polygon"];
reg = Identity @@ Identity @@ reg;
reg = First@MaximalBy[reg, Length];
region = MeshRegion[reg, Polygon[Range[Length[reg]]]];
rmf = RegionMember[region];
citiesloc = Select[citiesloc, rmf];
ccf = Nearest[citiesloc];
I now create a grid of points in the coordinates of france, and find for each the nearest city. I filter then any duplicates out. Lastly I show a map:
bounds = CoordinateBounds[reg];
n = {60, 60};
pts = MapThread[Subdivide[#1[[1]], #1[[2]], #2] &, {bounds, n - 1}];
pts = Tuples[pts];
pts = DeleteDuplicates[First@*ccf /@ pts];
pts // Length
(*dest=Lyon (city)["Coordinates"]*)
dest = {45.76`, 4.83`};
Graphics[{{EdgeForm[Black], FaceForm[LightBlue], Polygon[Reverse /@ reg]}, Point[Reverse /@ pts], Style[Point[Reverse@dest], Red, PointSize[Large]]}]
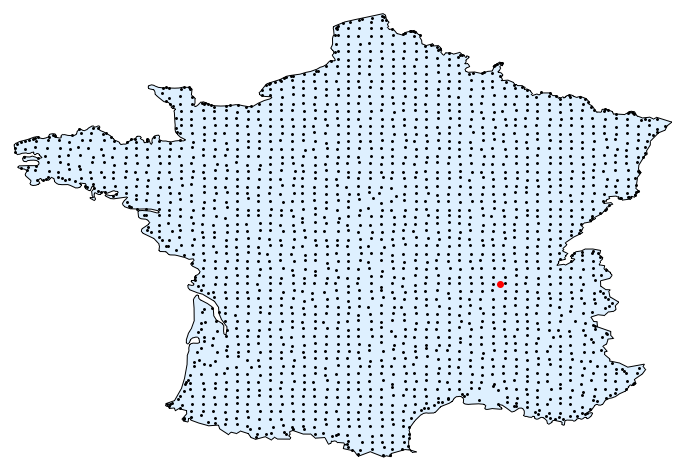
Now we have to calculate the route from any black point to Lyon (in red). This is very easy with the TravelDirections function (introduced v10.3).
ClearAll[SavePath]
SavePath[loc1:{lat_,lon_},loc2:{lat2_,lon2_},fnout_String]:=Block[{td},
td=Check[TravelDirections[{GeoPosition[loc1],GeoPosition[loc2]}],"fail"];
If[td=!="fail",
td=td["TravelPath"][[1,1]];
Export[fnout,td]
,
Print["Failed "<> fnout]
]
]
fnsout=ToString[#]<>".wdx"&/@Range[Length[pts]];
MapThread[SavePath[#1,dest,#2]&,{pts,fnsout}]
I let it run (this goes over the internet and the Wolfram servers give us the routes back) and the routes are saved to WDX files. Sorry for overloading the servers... ~10 or so failed for whatever reason. No worries, doesn't matter so much. In total 2165 did work. Now let's plot it!
We load in all the data (and filter those out that are too small (they returned $Failed or so):
SetDirectory[NotebookDirectory[]];
$HistoryLength = 2;
fns = FileNames["*.wdx"];
alldata = Import /@ fns;
alldata = Select[alldata, ByteCount[#] > 500 &];
Now let's count the road pieces:
pieces = Partition[DeleteDuplicates[Flatten[#, 1]], 2, 1] & /@ alldata;
pieces = Flatten[pieces, 1];
pieces = Round[pieces 10^11];
tpieces = Tally[pieces];
tpieces = GatherBy[tpieces, Last];
tpieces = SortBy[tpieces, Part[#, 1, -1] &];
widths = tpieces[[All, 1, -1]];
tpieces = tpieces[[All, All, 1]];
tpieces = Split[#, Last[#1] == First[#2] &] & /@ tpieces;
tpieces = Map[DeleteDuplicates[Flatten[#, 1]] &, tpieces, {2}];
tpieces /= 10^11.0;
What happens here? Well, first I take every route and flatten it, remove duplicates, and then cut it up in to pieces of length 2 (Partition[...,2,1]). Then I pile up all those little pieces (line 2). Because of rounding and so on I will round the coordinates and do so by multiplying them to make it very big integers). Now I tally all the small road-pieces to see how 'busy' they are. And then I group all the road-pieces that are equally busy (GatherBy[...]). And then Sort by the busyness of it (SortBy[...]). I save the busyness for later in the variable widths. Now I drop all the busyness-values, and now make the plotting a little easier by merging pieces of road, and removing duplicates. Lastly, I undo the rounding/multiplying.
Lastly we plot the result:
GeoGraphics[MapThread[{Thickness[0.0008 #1^0.3], GeoPath[#2, "TravelPath"]} &, {widths, tpieces}], ImageSize -> 1000]

Looks pretty cool! I just wanted to share this because it is (to me at least) really amazing that you can just do this within 50 lines or so and it took me 30 minutes or so to write it! Imagine doing this in C, Python, Java, Swift, ....!