Thanks for reporting this, @Clayton Shonkwiler we will add this to the list of small issues we have with editor and address at a Community update. I by the way quite enjoyed this GIF, I love building objects on trajectories - I call them "rails". I find that for nice visual feel sometimes it is worth to show the rails:
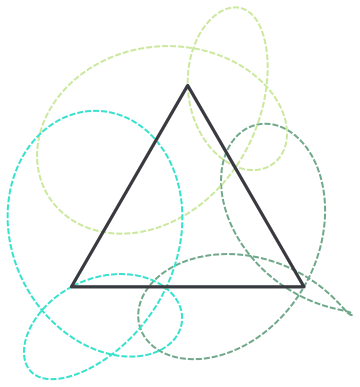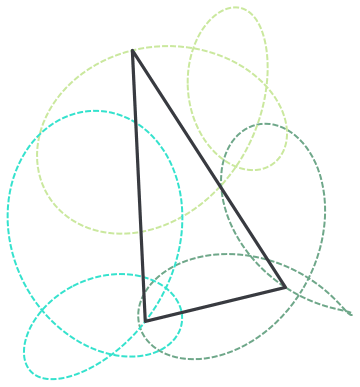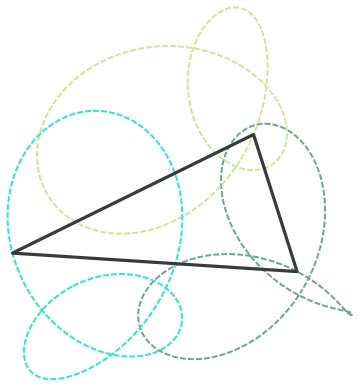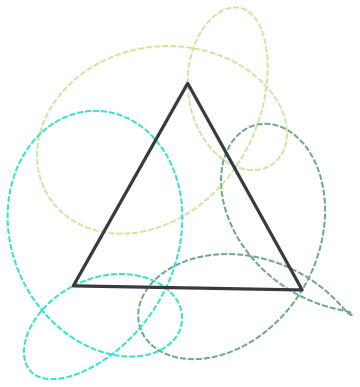
ToComplex[{x_, y_}] := x + I y;
ToReal[z_] := {Re[z], Im[z]};
FrameToEdges[frame_] := ToReal[ToComplex[#]^2] & /@ Transpose[frame];
FrameToVertices[frame_] := Accumulate[FrameToEdges[frame]];
data = Table[
Module[{mat, frame, rotatedframe, verts, com},
mat = RotationMatrix[t, {Cos[θ] Sin[φ], Sin[θ] Sin[φ], Cos[φ]}] /. {θ -> 3 π/4, φ -> 3 π/4};
frame = Transpose[ToReal[Sqrt[#]] & /@ (E^(I #)*2/3 & /@ Range[0, 4 π/3, 2 π/3])];
rotatedframe = frame.Transpose[mat];
verts = FrameToVertices[rotatedframe];
com = Mean[verts];
verts = RotationMatrix[t].# & /@ (# - com & /@ verts)
], {t, 0, 2 π, .03}];
rail = Graphics[{Dashed, Thick, RandomColor[], Line[#]} & /@ Transpose[data]]
Manipulate[
Module[{mat, frame, rotatedframe, verts, com},
mat = RotationMatrix[t, {Cos[θ] Sin[φ], Sin[θ] Sin[φ], Cos[φ]}] /. {θ -> 3 π/4, φ -> 3 π/4};
frame = Transpose[ToReal[Sqrt[#]] & /@ (E^(I #)*2/3 & /@ Range[0, 4 π/3, 2 π/3])];
rotatedframe = frame.Transpose[mat];
verts = FrameToVertices[rotatedframe];
com = Mean[verts];
verts = RotationMatrix[t].# & /@ (# - com & /@ verts);
Show[
rail,
Graphics[{FaceForm[None],
EdgeForm[
Directive[RGBColor["#383a40"], Thickness[.009],
JoinForm["Round"]]], Polygon[verts]}, PlotRange -> .8,
ImageSize -> 540, Background -> RGBColor["#F9F9F9"]]
]], {t, 0, 2 π}]