Message Boards Message Boards

Using Mathematica to see the world in a different light - part I

The international year of light has just drawn to an end. From 4-6 February the closing ceremony took place in Merida, Yukatan. 

GeoGraphics[GeoMarker[Entity["City", {"Merida", "Yucatan", "Mexico"}]], GeoRange -> Quantity[3000, "Kilometers"], GeoBackground -> "ReliefMap"]

enter image description here

The international Year of Light was a global initiative of the United Nations to celebrate light and light based technologies. Mathematica's built-in Wikipedia data contains detailed information on the Year of Light; here is the first sentence of the article. 

TextSentences[WikipediaData["Year of Light"]][[1]]

The International Year of Light and Light-based Technologies, 2015 (IYL 2015) is a United Nations observance that aims to raise awareness of the achievements of light science and its applications, and its importance to humankind.

I am planning to write three posts to show how the Wolfram Language, its wealth of data, and connected devices can be used to keep the year of light alive at your home. In this first part, I will use a spectrometer, connect it to the Wolfram Language, and try to "see the world in a different light". It turns out that the Wolfram Language will be as important as the hardware for this project.

Light is key to life on earth and sight is a key sense; most of the information our brains process comes from our vision. When the first organism developed primitive vision, that was an enormous evolutionary advantage, allowing them to escape preditors and localise prey. Light plays a crucial role in our modern lifes - most likely the information on this very website was delivered to you using optical fibres and light. Light also allows us to study everything from the smallest particles up to the farthest reaches of the universe.

In the 17th century Sir Isaac Newton introduced the word "spectrum" into optics, referring to the range of colours observed whey light passed through a prism. Today spectrometers are used in many scientific labs to study everything from molecules to the light of stars. In this Community several posts have described the construction of spectrometers and raspberry pi spectrometers. For this blog I will use a commercial, small spectrometer, the C12666MA Micro-Spectrometer, that attaches to an Arduino Uno. Hooking it up to the Arduino is trivial as the pins nicely align.

enter image description here

I will first upload the following code to the Arduino:

// This code is a modified from the original sketch from Peter Jansen
// https://github.com/tricorderproject/arducordermini
// This code removes the external ADC and uses the internal ADC instead. 
// also this code just prints the output to csv output to the terminal. 

#define SPEC_GAIN        A0
//#define SPEC_EOS         NA
#define SPEC_ST          A1
#define SPEC_CLK         A2
#define SPEC_VIDEO       A3
#define WHITE_LED        A4
#define LASER_404        A5

#define SPEC_CHANNELS    256
uint16_t data[SPEC_CHANNELS];

void setup() {

  //pinMode(SPEC_EOS, INPUT);
  pinMode(SPEC_GAIN, OUTPUT);
  pinMode(SPEC_ST, OUTPUT);
  pinMode(SPEC_CLK, OUTPUT);

  pinMode(WHITE_LED, OUTPUT);
  pinMode(LASER_404, OUTPUT);
  digitalWrite(WHITE_LED, LOW);
  digitalWrite(LASER_404, LOW);


  //digitalWrite(WHITE_LED, HIGH);
  //digitalWrite(LASER_404, HIGH);

  digitalWrite(SPEC_GAIN, HIGH);
  digitalWrite(SPEC_ST, HIGH);
  digitalWrite(SPEC_CLK, HIGH);
  digitalWrite(SPEC_GAIN, HIGH); //LOW Gain
  //digitalWrite(SPEC_GAIN, LOW); //High Gain

  //Serial.begin(9600);
  Serial.begin(115200);
}

void readSpectrometer()
{
  //int delay_time = 35;     // delay per half clock (in microseconds).  This ultimately conrols the integration time.
  int delay_time = 1;     // delay per half clock (in microseconds).  This ultimately conrols the integration time.
  int idx = 0;
  int read_time = 35;      // Amount of time that the analogRead() procedure takes (in microseconds) (different micros will have different times) 
  int intTime = 5; 
  int accumulateMode = false;
  int i;

  // Step 1: start leading clock pulses
  for (int i = 0; i < SPEC_CHANNELS; i++) {
    digitalWrite(SPEC_CLK, LOW);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, HIGH);
    delayMicroseconds(delay_time);
  }

  // Step 2: Send start pulse to signal start of integration/light collection
  digitalWrite(SPEC_CLK, LOW);
  delayMicroseconds(delay_time);
  digitalWrite(SPEC_CLK, HIGH);
  digitalWrite(SPEC_ST, LOW);
  delayMicroseconds(delay_time);
  digitalWrite(SPEC_CLK, LOW);
  delayMicroseconds(delay_time);
  digitalWrite(SPEC_CLK, HIGH);
  digitalWrite(SPEC_ST, HIGH);
  delayMicroseconds(delay_time);

  // Step 3: Integration time -- sample for a period of time determined by the intTime parameter
  int blockTime = delay_time * 8;
  long int numIntegrationBlocks = ((long)intTime * (long)1000) / (long)blockTime;
  for (int i = 0; i < numIntegrationBlocks; i++) {
    // Four clocks per pixel
    // First block of 2 clocks -- measurement
    digitalWrite(SPEC_CLK, LOW);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, HIGH);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, LOW);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, HIGH);
    delayMicroseconds(delay_time);

    digitalWrite(SPEC_CLK, LOW);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, HIGH);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, LOW);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, HIGH);
    delayMicroseconds(delay_time);
  }


  // Step 4: Send start pulse to signal end of integration/light collection
  digitalWrite(SPEC_CLK, LOW);
  delayMicroseconds(delay_time);
  digitalWrite(SPEC_CLK, HIGH);
  digitalWrite(SPEC_ST, LOW);
  delayMicroseconds(delay_time);
  digitalWrite(SPEC_CLK, LOW);
  delayMicroseconds(delay_time);
  digitalWrite(SPEC_CLK, HIGH);
  digitalWrite(SPEC_ST, HIGH);
  delayMicroseconds(delay_time);

  // Step 5: Read Data 2 (this is the actual read, since the spectrometer has now sampled data)
  idx = 0;
  for (int i = 0; i < SPEC_CHANNELS; i++) {
    // Four clocks per pixel
    // First block of 2 clocks -- measurement
    digitalWrite(SPEC_CLK, LOW);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, HIGH);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, LOW);

    // Analog value is valid on low transition
    if (accumulateMode == false) {
      data[idx] = analogRead(SPEC_VIDEO);
    } else {
      data[idx] += analogRead(SPEC_VIDEO);
    }
    idx += 1;
    if (delay_time > read_time) delayMicroseconds(delay_time - read_time);   // Read takes about 135uSec

    digitalWrite(SPEC_CLK, HIGH);
    delayMicroseconds(delay_time);

    // Second block of 2 clocks -- idle
    digitalWrite(SPEC_CLK, LOW);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, HIGH);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, LOW);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, HIGH);
    delayMicroseconds(delay_time);
  }

  // Step 6: trailing clock pulses
  for (int i = 0; i < SPEC_CHANNELS; i++) {
    digitalWrite(SPEC_CLK, LOW);
    delayMicroseconds(delay_time);
    digitalWrite(SPEC_CLK, HIGH);
    delayMicroseconds(delay_time);
  }
}

void print_data()
{
  for (int i = 0; i < SPEC_CHANNELS; i++) 
  {
    Serial.print(data[i]);
    Serial.print(',');
  }
  Serial.print("\n");
}

void loop() 
{
//  digitalWrite(LASER_404, HIGH);
//  readSpectrometer();
//  digitalWrite(LASER_404, LOW);
//  print_data();
//  delay(10);

//  digitalWrite(WHITE_LED, HIGH);
//  readSpectrometer();
//  digitalWrite(WHITE_LED, LOW);
//  print_data();
//  delay(10);

  readSpectrometer();
  print_data();
  delay(10);   
}

The Arduino code is quite long and I first thought to only attach it to the post, but there is a particular line which is important. In the "void readSpectrometer()" part there is the line

int intTime = 5;

which allows you to set the integration time, i.e. the exposure time. That is a very important parameter to get optimal results. With the new features of the Wolfram Language and in particular with the Arduino Device Connection it is possible to adjust the exposure from within the Wolfram Language code. For this post this is not really necessary, so I will save that for another day.

Connecting the Arduino-Spectrometer duo to Mathematica is trivial. Here I connect it to an OSX system.

mySpectrometer = DeviceOpen["Serial", {Quiet[FileNames["tty.usb*", {"/dev"}, Infinity]][[1]], "BaudRate" -> 115200}]

This piece of code

Quiet[FileNames["tty.usb*", {"/dev"}, Infinity]][[1]]

facilitates the connection as it detects the correct device automatically. We can now start collecting data like so:

data = Table[Pause[2]; ToExpression /@ StringSplit[FromCharacterCode[SplitBy[DeviceReadBuffer[mySpectrometer], # == 10 &][[-2]]], ","], {i, 6}];

This data aquisition code actually measures 6 spectra and pauses for 2 seconds between individual measurements. These repeated measurements decrease the noise of the measurements. The measurement procedure is very straight foward. You point the spectrometer at an object and execute the data aquisition. Let's fist look at the spectrum of a fluorescent light bulb. 

ListLinePlot[N@Mean[Select[data, Length[#] == 256 &]], PlotRange -> All]

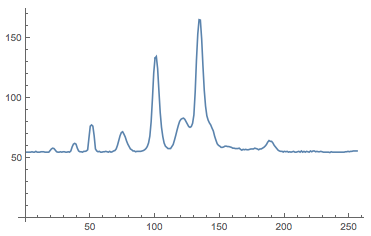
enter image description here

There are several peaks that we will try to understand a little bit later. The x-axis shows 256 bins which represent the different colours, i.e. frequencies. The y-axis shows the count, i.e. the intensity of that frequency band. In oder to be able to interpret the results we first need to calibrate the spectrometer. Here is a link to a table which contains calibration information for various versions of the spectrometer. It turns out that the calibration is performed using a 5th order polynomial; the repective coefficients are given in the calibration table. For my particular spectrometer I obtain:

a0 = 3.170083173*10^2;
b1 = 2.39519817;
b2 = -8.618615345*10^(-4);
b3 = -5.978279712*10^(-6);
b4 = 8.585352787*10^(-9);
b5 = -2.048534811*10^(-12);
wavelength[x_] := a0 + b1  x + b2  x^2 + b3  x^3 + b4*x^4 + b5  x^5

Here is a plot of the calibration curve:

Plot[{wavelength[x]}, {x, 0, 256}]

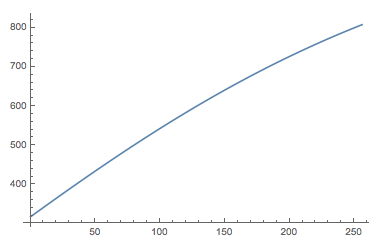
enter image description here

It transforms the number of the bin to the corresponding wavelength. We can not plot the spectrum with the correct x-axis.

datacalibrated = Transpose@{wavelength /@ Range[256], N@Mean[Select[data, Length[#] == 256 &]]};
ListLinePlot[datacalibrated, PlotRange -> All]

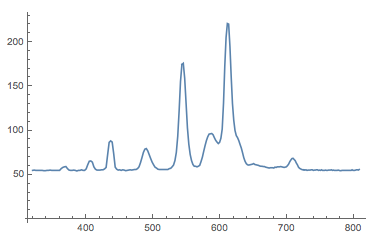
enter image description here

This is much better. This is how a professional spectrum of a fluorescent light bulb looks like:

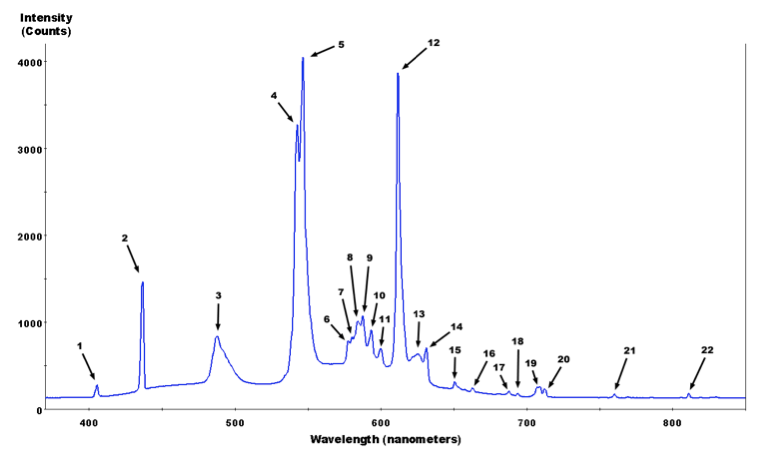
enter image description here

which is taken from the Wikipedia commons. Here is a list of the peaks and what element they correspond to:

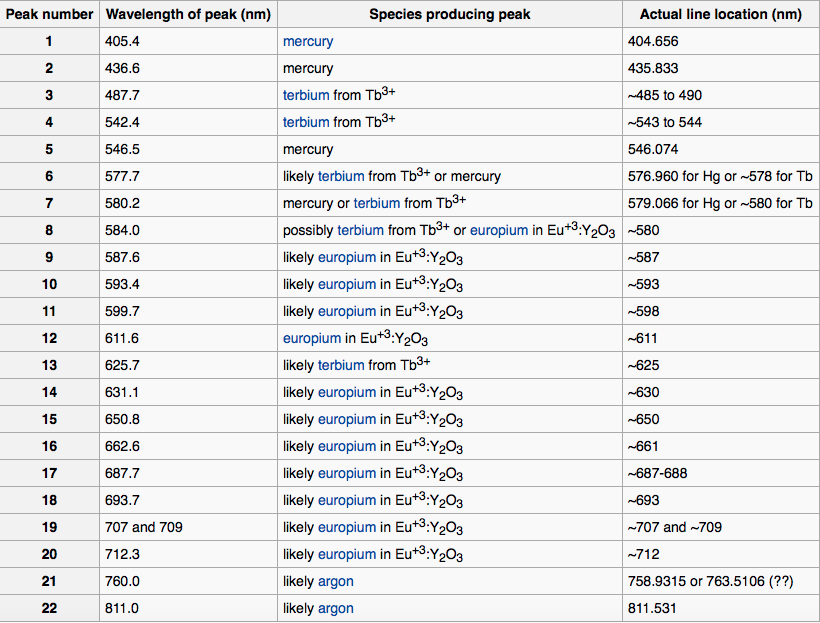
enter image description here

We clearly see the peaks for Mercury, Terbium and Europium. Wolfram|Alpha has a wealth of information about spectral lines and we can use the following line to get it.

WolframAlpha["spectral lines mercury"]

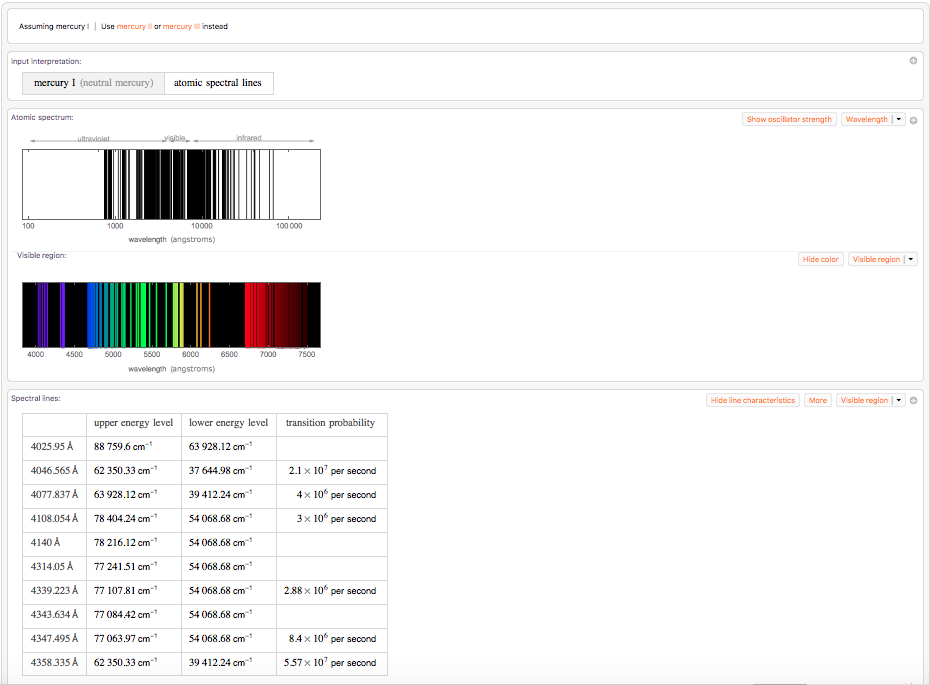
enter image description here

The two dominant lines here are the one at 4046.565 Angstrom and at 4358.335 Angstrom. They correspond to our lines at about 405 nm and 436 nm. Unfortunately, I have failed to extract a list of all relevant spectral lines from Wolfram|Alpha.

Let's try to spice our representation of the spectrum up a bit. It would be nice to have a visual cue as to the colour the different wavelengths correspond to. Mathematica and the Wolfram Language have everything built in to make this task really easy:

ColorData["VisibleSpectrum"][#] & /@ datacalibrated[[All, 1]]

enter image description here

We can now merge this into a band of colours that we can plot with the spectrum.

Graphics[Table[{ColorData["VisibleSpectrum"][datacalibrated[[i, 1]]], Rectangle[{datacalibrated[[i, 1]], 0}, {datacalibrated[[i + 1, 1]],40}]}, {i, 1, Length[datacalibrated] - 1}]]

enter image description here

If we plot this together things start being easier to interpret. 

Show[ListLinePlot[datacalibrated, PlotRange -> All], Graphics[Table[{ColorData["VisibleSpectrum"][datacalibrated[[i, 1]]],
     Rectangle[{datacalibrated[[i, 1]], 10}, {datacalibrated[[i + 1, 1]], 40}]}, {i, 1, Length[datacalibrated] - 1}]]]

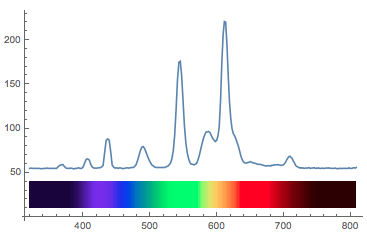
enter image description here

Now there are two more things I want to tweak. First of all there is this off-set of 54; that is a "zero count", i.e. I obtain at least 54 even if there is no signal so I need to subtract that. This number depends on the spectrometer that you have. On a second one I have got that value is different. Also, I would like the lightcurve itself to reflect the colour. The following code achieves that:

Show[ListLinePlot[Evaluate@(Plus[{0., -54.}, #] & /@ datacalibrated), 
  PlotRange -> {All, {-30, All}}, Joined -> True, Frame -> True, 
  ColorFunction -> (Blend["VisibleSpectrum", #1* Differences[datacalibrated[[All, 1]][[{1, -1}]]][[1]] + 
  datacalibrated[[1, 1]]] &), Filling -> Axis, LabelStyle -> Directive[Black, Bold, Medium], 
  FrameLabel -> {"Wavelength (nm)", "Intensity"}], Graphics[Table[{ColorData["VisibleSpectrum"][datacalibrated[[i, 1]]],
     Rectangle[{datacalibrated[[i, 1]], -30}, {datacalibrated[[i + 1, 1]], -10}]}, {i, 1, Length[datacalibrated] - 1}]]]

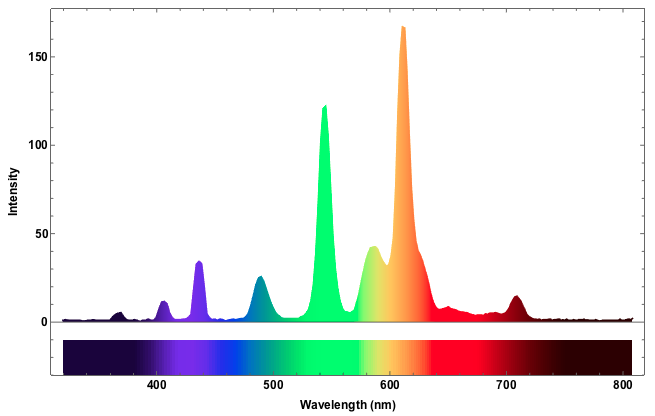
enter image description here

To identify the spectral lines it is useful to identify maxima of the curve. The following function helps to achieve that:

localMaxPositions = 
  Compile[{{pts, _Real, 1}}, 
   Module[{result = Table[0, {Length[pts]}], i = 1, ctr = 0}, For[i = 2, i < Length[pts], i++, 
     If[pts[[i - 1]] < pts[[i]] && pts[[i + 1]] < pts[[i]],result[[++ctr]] = i]];Take[result, ctr]]];

We can now locate the maxima and plot that on the curve:

dplot = ListLinePlot[datacalibrated, PlotRange -> All];
maxs = ListPlot[Select[Nest[#[[localMaxPositions[#[[All, 2]]]]] &, datacalibrated, 1], #[[2]] > 58.33 &], PlotStyle -> Directive[PointSize[0.015], Green]];
Show[{dplot, maxs}]

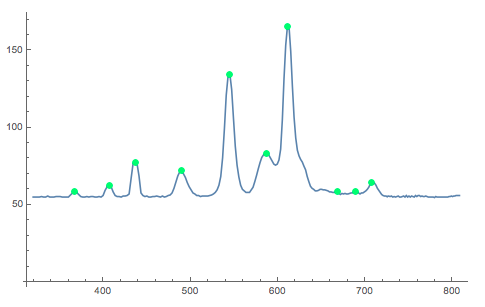
enter image description here

The following function produces a list of the positons of the maxima:

Select[Nest[#[[localMaxPositions[#[[All, 2]]]]] &, datacalibrated, 1], #[[2]] > 58.33 &][[All, 1]]
(*{366.873694406445`,406.4710188519941`,436.1860721777116`,489.\
5449068238321`,544.8439203380104`,587.3854766583466`,610.\
7844904587837`,668.0095922519685`,688.8768717778272`,707.\
3639428495288`}*)

It turns out that there is a packages which contains information about spectral lines, but the elements that we are interested in (Hg, Te, Eu) are not in the database. For elements that are in the database we can compare the measured lines to the ones in the database:

<< ResonanceAbsorptionLines`
ElementAbsorptionMap[Na]

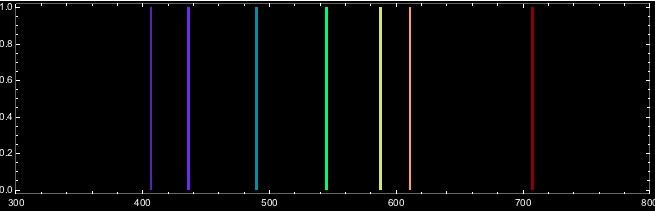
enter image description here

What we can do, however, is to generate - or simulate- an approximatio of the spectral lines we measure. There is a discussion on Stackexchange that shows how to plot an emission spectrum. The following lines are taken from that discussion. 

spec[wavelength_, width_] := Flatten[Table[{{x, 0, x}, {x, 1, x}}, {x, wavelength - width, wavelength + width, 0.1}], 1];
ListDensityPlot[
 spec[#, 1] & /@ 
  Select[Nest[#[[localMaxPositions[#[[All, 2]]]]] &, datacalibrated, 
     1], #[[2]] > 59.33 &][[All, 1]], 
 ColorFunction -> ColorData["VisibleSpectrum"], 
 ColorFunctionScaling -> False, AspectRatio -> .3, 
 PlotRange -> {{300, 800}}, 
 FrameTicks -> {Automatic, None, None, None}, 
 FrameTicksStyle -> White, Frame -> True, Background -> Black]

enter image description here

Case Studies

Blue sky

I now measure the spectrum of the blue sky. The measurement was taken late in the year and the sky wasn't the "bluest of blues", but we can still make out some interesting features.

mySpectrometer = 
  DeviceOpen[
   "Serial", {Quiet[FileNames["tty.usb*", {"/dev"}, Infinity]][[1]], 
    "BaudRate" -> 115200}];
datasky = 
  Table[Pause[2]; 
   ToExpression /@ 
    StringSplit[
     FromCharacterCode[
      SplitBy[DeviceReadBuffer[mySpectrometer], # == 10 &][[-2]]], 
     ","], {i, 6}];
a0 = 3.170083173*10^2;
b1 = 2.39519817;
b2 = -8.618615345*10^(-4);
b3 = -5.978279712*10^(-6);
b4 = 8.585352787*10^(-9);
b5 = -2.048534811*10^(-12);
wavelength[x_] := a0 + b1  x + b2  x^2 + b3  x^3 + b4*x^4 + b5  x^5;
datacalibratedsky = 
  Transpose@{wavelength /@ Range[256], N@Mean[Select[datasky, Length[#] == 256 &]]};
Show[ListLinePlot[Evaluate@(Plus[{0., -54.}, #] & /@ datacalibratedsky), 
  PlotRange -> {All, {-30, All}}, Joined -> True, Frame -> True, ColorFunction -> (Blend["VisibleSpectrum", #1*Differences[datacalibratedsky[[All, 1]][[{1, -1}]]][[1]] + datacalibratedsky[[1, 1]]] &), Filling -> Axis, LabelStyle -> Directive[Black, Bold, Medium], FrameLabel -> {"Wavelength (nm)", "Intensity"}], 
 Graphics[Table[{ColorData["VisibleSpectrum"][datacalibratedsky[[i, 1]]], Rectangle[{datacalibratedsky[[i, 1]], -30}, {datacalibratedsky[[i + 1, 1]], -10}]}, {i, 1, Length[datacalibratedsky] - 1}]]]

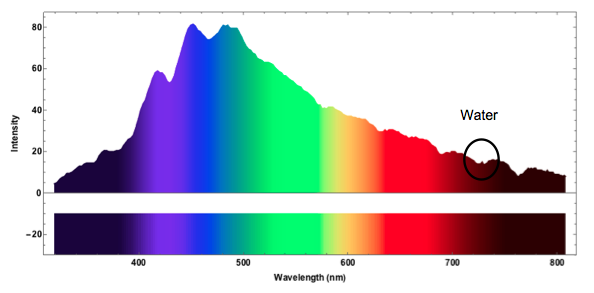
enter image description here

The spectrum clearly shows the "blue" in the sky. It turns out that the marked double dip corresponds to absorption by water.

Lasers

Using exactly the same code we can now analyse the spectrum of different lasers - red, green and blue. We can clearly see that the red and green lasers have a very narrow peak within the red and green spectral bands, whereas the blue laser has a much broader peak. This is probably related to how blue laser light is generateed in cheap laser pointers.

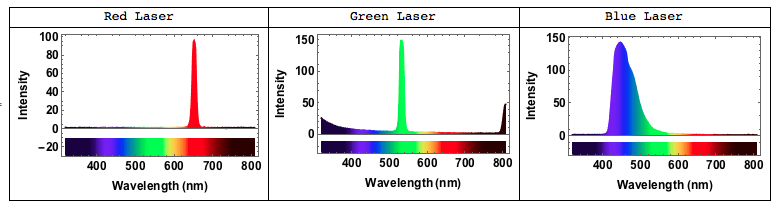
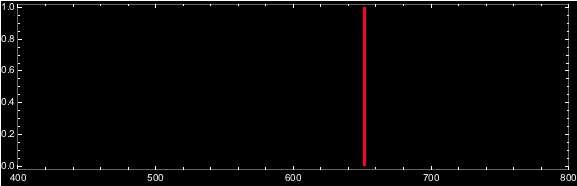
enter image description here

Here is how the spectrum of a red laser would look like:

ListDensityPlot[
 spec[#, 1] & /@ 
  Select[Nest[#[[localMaxPositions[#[[All, 2]]]]] &, datacalibratedlaserr, 1], #[[2]] > 59.33 &][[All, 1]], 
 ColorFunction -> ColorData["VisibleSpectrum"], ColorFunctionScaling -> False, AspectRatio -> .3, 
 PlotRange -> {{400, 800}}, FrameTicks -> {Automatic, None, None, None}, 
 FrameTicksStyle -> White, Frame -> True, Background -> Black]

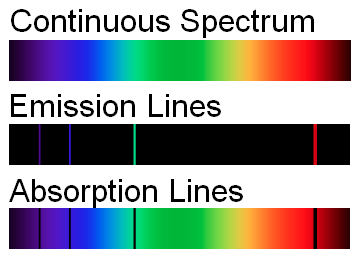
enter image description here

Absorption spectrum - green leaf

Up to now we have maily discussed emission spectra - apart from some features of the blue sky example. Let's now generate an absorption spectrum. In an emission spectrum a material actively emits radiation/light. In an absoprtion spectrum light that passes through the material.

enter image description here

In order to produce a good absorption spectrum we would ideally use a light source that produces a strong continuous spectrum. When I conducted the leaf experiment I only had a very cheap lamp which is usually used by doctors for initial examinations:

enter image description here

I pointed the lamp at a green leaf and measured the light that shone through. The problem was that the lamp did produce a very poor spectrum heavily biased towards the red frequency range. So in this case study I will first measure the emission spectrum of the lamp and then normalise the absorption spectrum of the leaf. Let's start with the lamp.

mySpectrometer = 
  DeviceOpen[
   "Serial", {Quiet[FileNames["tty.usb*", {"/dev"}, Infinity]][[1]], 
    "BaudRate" -> 115200}];
datalamp = 
  Table[Pause[2]; 
   ToExpression /@ 
    StringSplit[
     FromCharacterCode[
      SplitBy[DeviceReadBuffer[mySpectrometer], # == 10 &][[-2]]], 
     ","], {i, 6}];
a0 = 3.170083173*10^2;
b1 = 2.39519817;
b2 = -8.618615345*10^(-4);
b3 = -5.978279712*10^(-6);
b4 = 8.585352787*10^(-9);
b5 = -2.048534811*10^(-12);
wavelength[x_] := a0 + b1  x + b2  x^2 + b3  x^3 + b4*x^4 + b5  x^5;
datacalibratedlamp = 
  Transpose@{wavelength /@ Range[256], N@Mean[Select[datalamp, Length[#] == 256 &]]};
Show[ListLinePlot[Evaluate@(Plus[{0., -54.}, #] & /@ datacalibratedlamp), 
  PlotRange -> {All, {-30, All}}, Joined -> True, Frame -> True, ColorFunction -> (Blend["VisibleSpectrum", #1*Differences[datacalibratedlamp[[All, 1]][[{1, -1}]]][[1]] + datacalibratedlamp[[1, 1]]] &), Filling -> Axis, 
  LabelStyle -> Directive[Black, Bold, Medium], 
  FrameLabel -> {"Wavelength (nm)", "Intensity"}], 
 Graphics[Table[{ColorData["VisibleSpectrum"][datacalibratedlamp[[i, 1]]], 
 Rectangle[{datacalibratedlamp[[i,1]], -30}, {datacalibratedlamp[[i + 1, 1]], -10}]}, {i, 1,Length[datacalibratedlamp] - 1}]]]

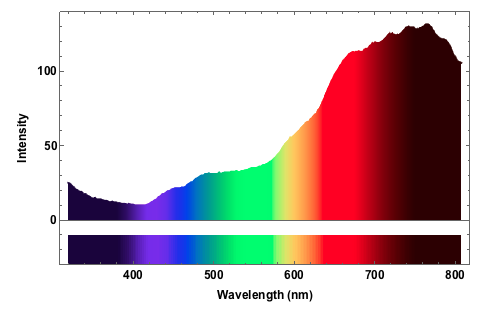
enter image description here

The spectrum is clearly biased to the red freqencies. In the blue/ultraviolet range the light source produces to little output that it will be impossible to determine a reasonable absorption spectrum there. Let's go on to measure the absorption of the leaf.

absorptionleaf = 
  Transpose[{datacalibratedleaf[[All, 1]], (datacalibratedleaf[[All, 2]]/datacalibratedlamp[[All, 2]])}];
Show[ListLinePlot[Evaluate@(Plus[{0., 0.}, #] & /@ absorptionleaf), PlotRange -> {All, {-0.3, 1}}, Joined -> True, Frame -> True, 
  ColorFunction -> (Blend["VisibleSpectrum", #1*Differences[absorptionleaf[[All, 1]][[{1, -1}]]][[1]] + absorptionleaf[[1, 1]]] &), Filling -> Axis, 
  LabelStyle -> Directive[Black, Bold, Medium], FrameLabel -> {"Wavelength (nm)", "Intensity"}], Graphics[Table[{ColorData["VisibleSpectrum"][absorptionleaf[[i, 1]]],Rectangle[{absorptionleaf[[i, 1]], -0.3}, {absorptionleaf[[i + 1,1]], -.1}]}, {i, 1, Length[absorptionleaf] - 1}]]]

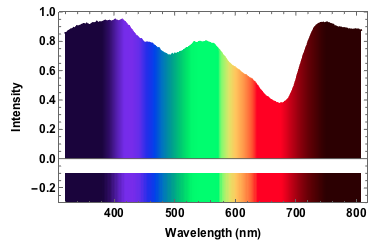
enter image description here

The absorption in the red frequency range stems from chlorophyll; chlorophyll also absorbs in the 400-450nm range which is hard to se here, because of our poor light source. The dip at around 500nm is carotenoids. You can compare that to the spectrum of leaves on this website.

"Black body radiation" - an old fashioned light bulb

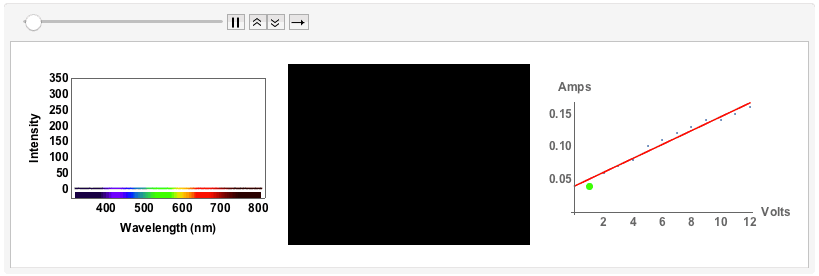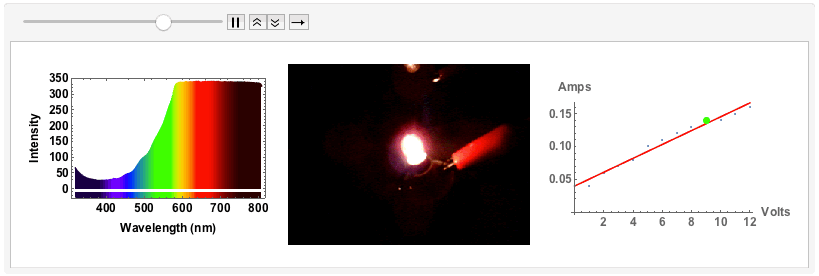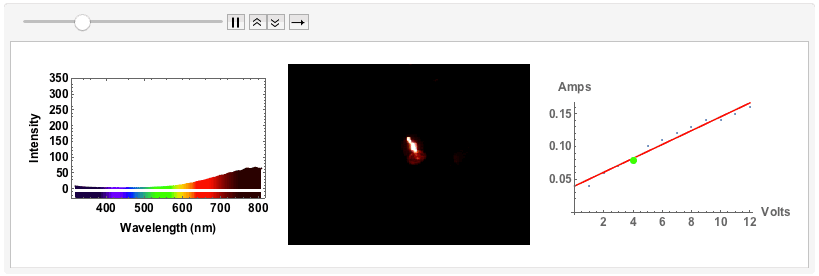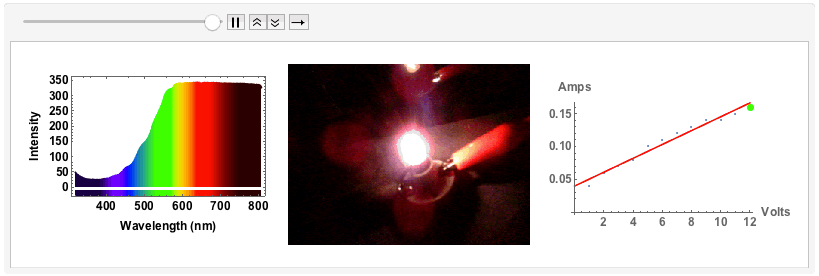
The final example will be of an old fashioned, small light bulb.

enter image description here

I will use a bench supply to slowly increase the voltage and the current. The filament will go from a red glowing colour to brighter "whiter" colour, but we will see that even for the highest voltage of 12V the spectrum will still be quite different from "white", i.e. uniform. The code is just the same as above. I save all plots for voltages 1V to 12V with increments of 1V in one variable:

specall = {spec1V, spec2V, spec3V, spec4V, spec5V, spec6V, spec7V, spec8V, spec9V, spec10V, spec11V, spec12V}

This can be easily plotted like so:

Grid[Partition[specall, 4]]

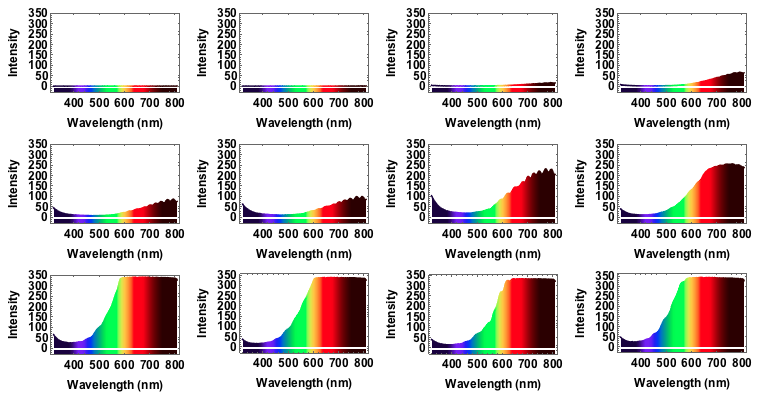
enter image description here

We can also animate this:

ListAnimate[specall, AnimationRunTime -> 10]

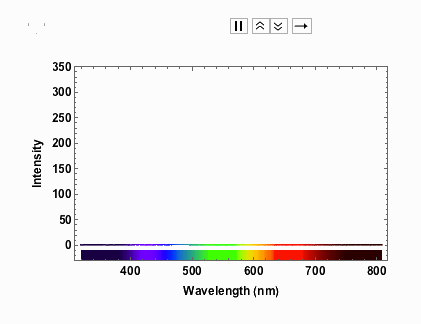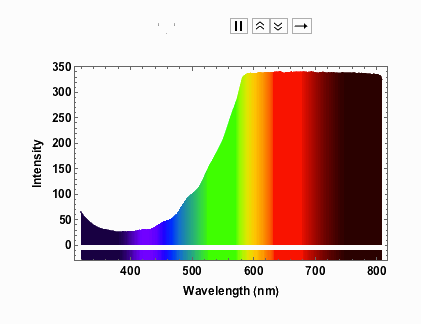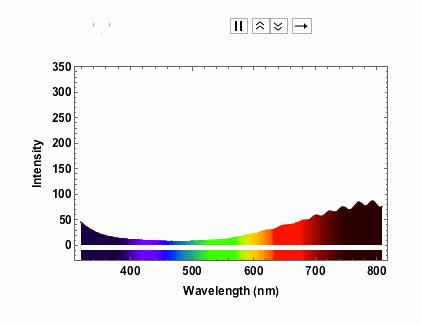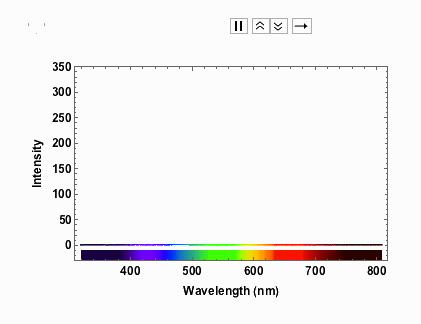
enter image description here

Note that from 9V onwards the spectrum has max-ed out. When I measured the spectra I took note of the voltage and the corresponding current:

voltageamp = {{1, 0.04}, {2, 0.06}, {3, 0.07}, {4, 0.08}, {5, 0.1}, {6, 0.11}, {7, 0.12}, {8, 0.13}, {9, 0.14}, {10, 0.14}, {11, 0.15}, {12, 0.16}}

I can now represent that with the regression line. 

Show[ListPlot[voltageamp, AxesLabel -> {"Volts", "Amps"}, LabelStyle -> Directive[Bold, Medium]], 
 Plot[Evaluate@Fit[voltageamp, {1, x}, x], {x, 0, 12}, PlotStyle -> Red]]

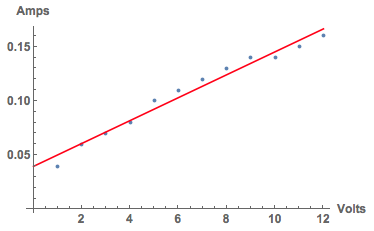
enter image description here

Note the nearly linear increase in current as the voltage increases. Finally, I took photos as the voltage increased.

enter image description here

We now add a little bit of motion to the voltage amp graph:

figvoltsamp = 
  Evaluate@Table[Show[ListPlot[voltageamp, AxesLabel -> {"Volts", "Amps"}, LabelStyle -> Directive[Bold, Medium], 
      Epilog -> {PointSize[Large], Green, Point[voltageamp[[i]]]}], Plot[Evaluate@Fit[voltageamp, {1, x}, x], {x, 0, 12}, PlotStyle -> Red]], {i, 1, 12}];

To finish everything off, we can now animate this:

ListAnimate[GraphicsRow[#, ImageSize -> Full] & /@ Transpose[{specall, bulb, figvoltsamp}]]

enter image description here

If we were to assume that this is the radiation of a black body, we could use Planck's law:

FormulaData[{"PlanckRadiationLaw", "Wavelength"}]

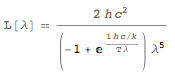
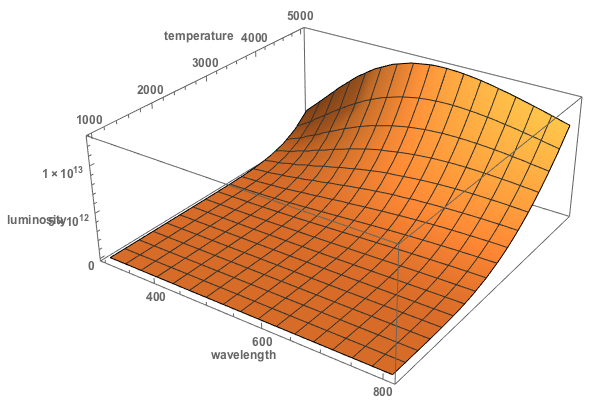
enter image description here

We could plot this as a function of temperature and wavelength

equation = 
  FormulaData[{"PlanckRadiationLaw", "Wavelength"}, {"T" -> Quantity[t, "Kelvins"], 
    "\[Lambda]" -> Quantity[l, "Nanometers"]}];
Plot3D[Quantity[1.191042*^29, ("Pascals")/("Seconds")]/(-1.`16.255 l^5 + 2.71828^(1.438*^7/(l t)) l^5), {l, 300, 808}, {t, 1000, 5000}, PlotRange -> All, 
 AxesLabel -> {"wavelength", "temperature", "luminosity"}, LabelStyle -> Directive[Bold, Medium], ImageSize -> Large]

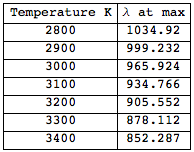
enter image description here

We can also write a little loop to calculate for which wavelength the maximum for different temperatures is reached.

results = {}; Monitor[
 Table[equation2 = FormulaData[{"PlanckRadiationLaw", 
 "Wavelength"}, {"T" -> Quantity[t, "Kelvins"], "\[Lambda]" -> Quantity[l, "Nanometers"]}]; 
  root = FindRoot[D[equation2[[2, 2]], l] == 0, {l, 700}, MaxIterations -> Infinity]; 
  AppendTo[results, {t, root}], {t, 2800, 3400, 100}], t]

This gives the following table:

Grid[Join[{{"Temperature K", "\[Lambda] at max"}}, Transpose[{results[[All, 1]], results[[All, 2, -1, 2]]}]], Frame -> All]

enter image description here

We can plot the relationship between maxium and temperature.

ListLinePlot[Transpose[{results[[All, 1]], results[[All, 2, -1, 2]]}],Mesh -> Full, MeshStyle -> Red, 
 AxesLabel -> {"Temperature", "wavelength at max"}, LabelStyle -> Directive[Bold, Medium], ImageSize -> Large]

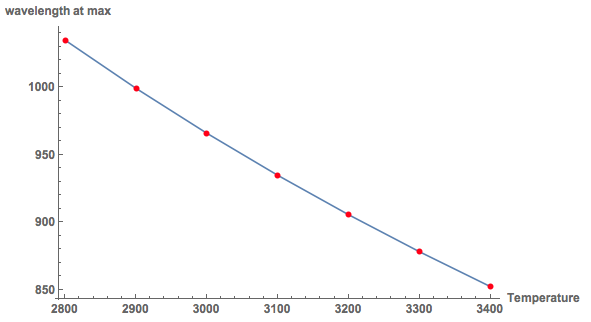
enter image description here

This allows us in principle to estimate the temperature of the filament. Note, that for 8V the maximum is at about 750nm. The graph shows that this corresponds to a temperature higher than 3400K, which is too high for such a small light bulb. So there is still quite some room for improvement... The principle of temperature measurement, by the colour of the sample is realistic.

There are many further projects one could think of. I suppose that with a decent telescope it should be possible to analyse the light of stars for example. Also, the spectrometer works nicely on a Raspberry Pi. It should be quite straight forward to take measurements of say the sky over the day and see how the dominant colours change.

Cheers,

Marco
POSTED BY: Marco Thiel
4 Replies
Sort By:

Awesome post, Marco! I'm looking forward to reading your other two posts to "see the world in a different light".
POSTED BY: Bernat Espigulé

enter image description here - another post of yours has been selected for the Staff Picks group, congratulations !

We are happy to see you at the tops of the "Featured Contributor" board. Thank you for your wonderful contributions, and please keep them coming!
POSTED BY: EDITORIAL BOARD

@Marco Thiel, amazing post as usual, and we excitingly adding it to Staff Picks! At some point you said:

I have failed to extract a list of all relevant spectral lines from Wolfram|Alpha

Did you mean the following code?

mercuryLINES = WolframAlpha["spectral lines mercury", {{"Lines:AtomicSpectrumData", 1}, "ComputableData"}];
TableForm[Rest[#[[1, 1]]], TableHeadings -> {None, First[#[[1, 1]]]}] &@mercuryLINES

enter image description here

You do not need to know the syntax of WolframAlpha function, just access it interactively (as explained here: Data Formats in Wolfram|Alpha):

enter image description here

enter image description here

enter image description here
POSTED BY: Vitaliy Kaurov

Dear @Vitaliy Kaurov ,

thank you very much for your kind and encouraging words. I am glad that you liked the post.

I was, in fact, aware that one can use Wolfram|Alpha and then click on the more button in the subpod. My problem is that the data I managed to download appears to be incomplete. If we use Wolfram|Alpha to display the spectrum of say mercury it looks like this:

enter image description here

There are spectral lines all over the visual range from 4000-7500 Angstroms. If I go to the pod content I only get the first lines. I can click on "More" and I get some more lines, but no matter how often I click on "More" I only get 21 lines:

lines=WolframAlpha["Spectral lines mercury", {{"Lines:AtomicSpectrumData", 1}, "ComputableData"}, PodStates -> {"Lines:AtomicSpectrumData__More"}]

So in a table this looks like this:

lines[[1, 1]] // TableForm

enter image description here

The last lines I download are at about 4700 Angstroms. That means that a large part of the visual spectrum is not covered in the list I download. I have tried various modifications of the Wolfram|Alpha request, but nothing downloaded all the visible lines. This is not a problem for elements that only have "few" spectral lines, but is more of a problem for those, like mercury, terbium etc that have lots of them. I am not terribly familiar with Wolfram|Alpha syntax and do not know whether there is a way to extract a list of all lines. I am aware that many of the lines are quite weak. Wolfram Alpha also has information on the intensity of the lines:

linesplus = WolframAlpha["spectrum mercury", {{"Lines:AtomicSpectrumData", 1}, "ComputableData"}, PodStates -> {"Lines:AtomicSpectrumData__Show line \characteristics"}];
linesplus[[1, 1]] // TableForm

enter image description here

The transition probability tells us which lines would be strong, i.e. strong enough to be seen with a cheap spectrometer; it appears that only the ones with transition probabilities of about $10^7$ are really easy to detect. I have also noted that the same requests I used above for mercury do not work equally well for all elements, say terbium.

The objective would be to input a spectrum, like the ones I have measured in the post. They I would like to compare that to a database of known spectra and program something that attempts to guess at what is contained in the sample. I have tried importing data from some spectral databases, like this one or this one or this one , but nothing really worked well enough. It would be nice to be able to detect these components from the spectrum. In a project we are doing here, we try to send the spectral data to mobile phones. If we could use CloudDeploy on these platforms, perhaps even on the Apple Watch, that would be nice.

We have seen many fantastic posts here where devices were hooked up to Mathematica and where data was read. Most of the time Mathematica is "only" used to represent data, stream the data online, read it from other deices etc. I wonder whether: (i) the Wolfram Language's abilities could be used even more to improve the data from poor devices, e.g. perform a sort of deconvolution on the spectra I got or do some tricks to mathematically improve the measurements, and (ii) I am looking for examples of how the Wolfram Language adds substantially to the analysis of the data. Being able to decompose the spectrum into the components would be a nice case study.

As I said, I will try to post at least two further examples and I hope that I'll be able to show how much the Wolfram Language can improve the data from poor sensors and perhaps more...

I'd love to hear your thoughts on this.

Best wishes,

Marco
POSTED BY: Marco Thiel
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract