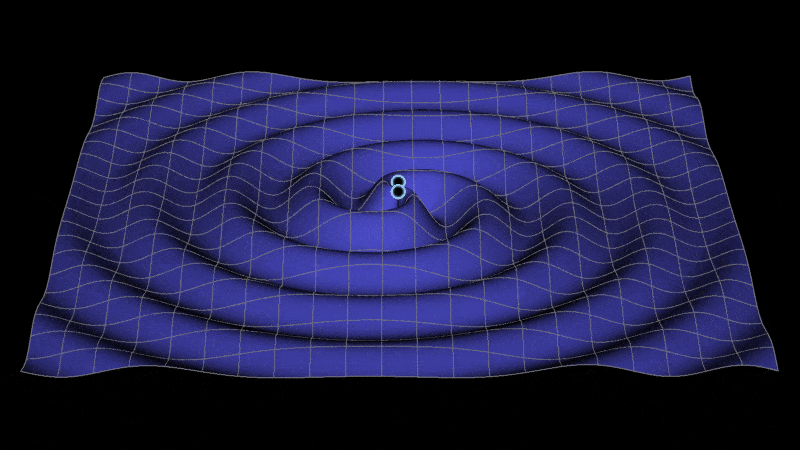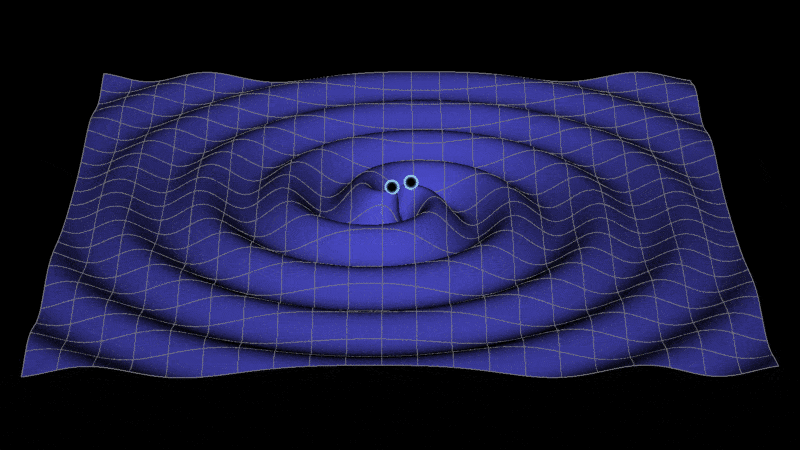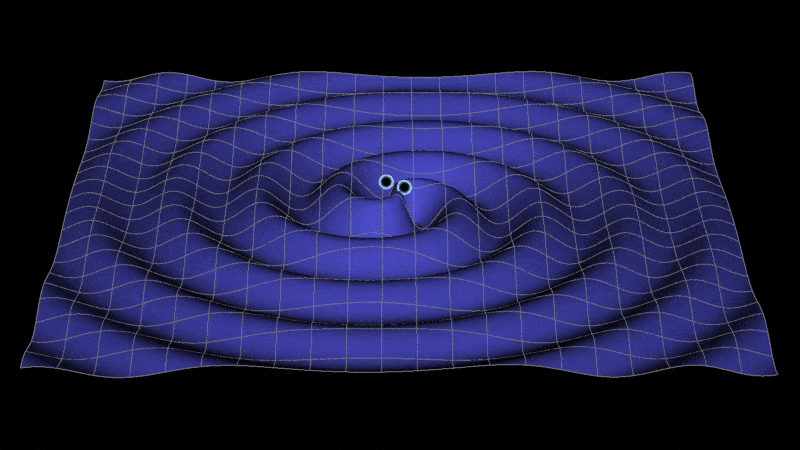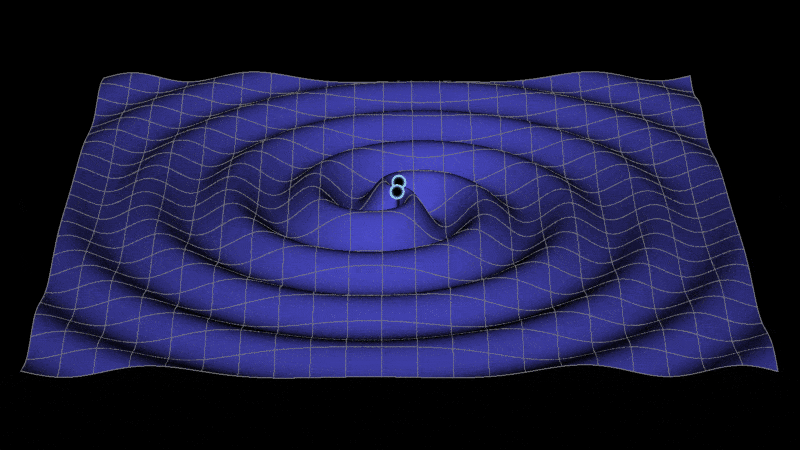
With all of the rumors and excitement about the gravity wave press release tomorrow, I was reminded of this code I've had lying around for years for creating a gravity wave visualization (seen above) for illustrative purposes. You can find also a video here. It was inspired by an interaction I had years ago (unfortunately I can't find the interaction in my email) with someone on the LISA project wanting to use Mathematica to re-create a visualization they had. This code was the result of that interaction.
First, the primary goal was to generate a "space-time" surface and mesh that had a double-armed spiral wave on it. The following code generates that. Its dependent on a rotation angle Theta which is not specified here:
Plot3D[(60 Cos[
2 ArcTan[y/(x + 0.00001)] - \[Theta] + 0.544331 Sqrt[x^2 + y^2]])/(
20 + Sqrt[x^2 + y^2]), {x, -45, 45}, {y, -45, 45}, PlotPoints -> 100,
Mesh -> 20, MeshStyle -> {RGBColor[.5, .5, .5, .5]}, Boxed -> False,
BoxRatios -> Automatic, Axes -> False,
PlotStyle -> {RGBColor[.3, .3, .8]}, ImageSize -> {1024, 768},
Lighting -> {{"Directional", White, ImageScaled[{0, 0, 2.}]}},
ViewPoint -> {-0.011, -3.043, 1.479}, Background -> Black,
BoundaryStyle -> RGBColor[.5, .5, .5, .5]]
I wanted to overlay 2 stars or black holes on top of the surface. Combining the above with this overlay and giving a value to the angle Theta we get:
With[{\[Theta] = 0},
Show[Plot3D[(
60 Cos[2 ArcTan[y/(x + 0.00001)] - \[Theta] +
0.544331 Sqrt[x^2 + y^2]])/(
20 + Sqrt[x^2 + y^2]), {x, -45, 45}, {y, -45, 45},
PlotPoints -> 100, Mesh -> 20,
MeshStyle -> {RGBColor[.5, .5, .5, .5]}, Boxed -> False,
BoxRatios -> Automatic, Axes -> False,
PlotStyle -> {RGBColor[.3, .3, .8]}, ImageSize -> {1024, 768},
Lighting -> {{"Directional", White, ImageScaled[{0, 0, 2.}]}},
ViewPoint -> {-0.011, -3.043, 1.479}, Background -> Black,
BoundaryStyle -> RGBColor[.5, .5, .5, .5]],
Graphics3D[{Directive[Hue[.58, 0, 1],
Lighting ->
Join[{{"Ambient", Black}},
Table[{"Directional", Hue[.58, .5, 1],
ImageScaled[{Sin[x], Cos[x], -.5}]}, {x, 0, 2 Pi - 2 Pi/8,
2 Pi/8}]]],
Sphere[{2 Cos[\[Theta] - \[Pi]/2], 2 Sin[\[Theta] - \[Pi]/2], 3},
1], Sphere[{Cos[\[Theta] + \[Pi]/2], Sin[\[Theta] + \[Pi]/2], 3},
1]}], PlotRange -> All]]
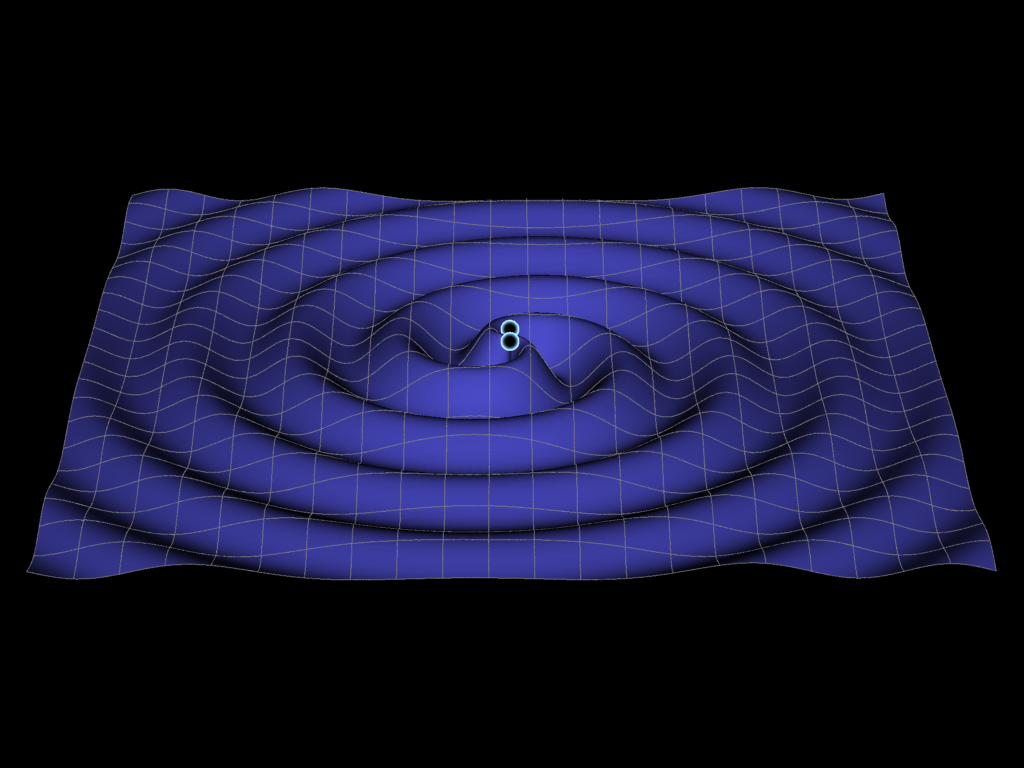
Next, I wanted to animate this to give the effect that the spiral arms are rotating outwards. That's done by incrementing the angle Theta and generating a list of frames that can then be exported.
anim = Table[
Rasterize[
Show[Plot3D[(
60 Cos[2 ArcTan[y/(x + 0.00001)] - \[Theta] +
0.544331 Sqrt[x^2 + y^2]])/(
20 + Sqrt[x^2 + y^2]), {x, -45, 45}, {y, -45, 45},
PlotPoints -> 100, Mesh -> 20,
MeshStyle -> {RGBColor[.5, .5, .5, .5]}, Boxed -> False,
BoxRatios -> Automatic, Axes -> False,
PlotStyle -> {RGBColor[.3, .3, .8]}, ImageSize -> {800, 450},
Lighting -> {{White, ImageScaled[{0, 0, 2.}]}},
ViewPoint -> {-0.011, -3.043, 1.479},
Background -> RGBColor[0, 0, 0], BoundaryStyle -> Gray],
Graphics3D[{Directive[Hue[.58, 0, 1],
Lighting ->
Join[{{"Ambient", Black}},
Table[{"Directional", Hue[.58, .5, 1],
ImageScaled[{Sin[x], Cos[x], -.5}]}, {x, 0, 2 Pi - 2 Pi/8,
2 Pi/8}]]],
Sphere[{2 Cos[\[Theta] - \[Pi]/2], 2 Sin[\[Theta] - \[Pi]/2],
3}, 1], Sphere[{Cos[\[Theta] + \[Pi]/2],
Sin[\[Theta] + \[Pi]/2], 3}, 1]}],
PlotRange -> All]], {\[Theta], 0, 2 \[Pi], .1}];
And then to export it to an animated GIF:
Export["GravityWave.gif", anim]
The result is the animation at the top of this post.