Yes, that is exactly what it says in the documentation of Matlab! This community is on Mathematica. Both products have different functions and syntax. It is very unlikely that Matlab code will work directly in Mathematica. :-)

Cheers,

Marco

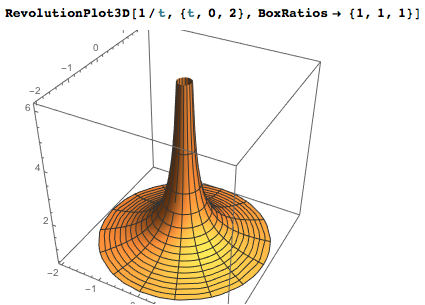
• Method 1: Use the build-in RevolutionPlot3D function:

  RevolutionPlot3D[1/t, {t, 0, 2}, BoxRatios -> {1, 1, 1}]
  

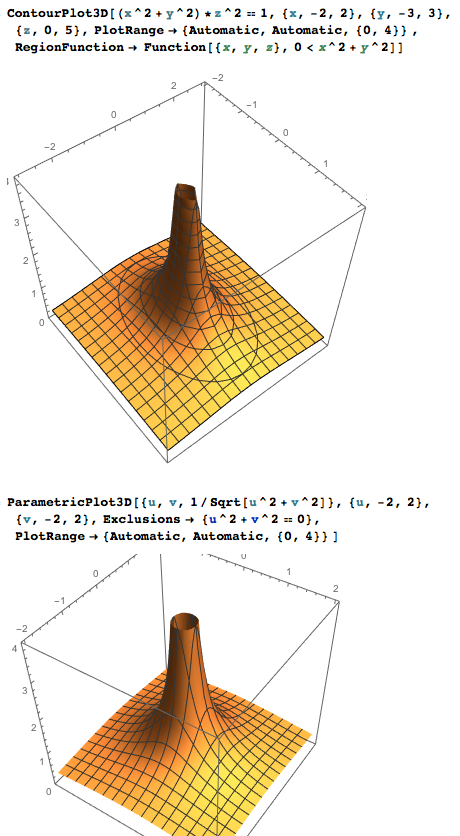
• Method 2:

  ContourPlot3D[(x^2 + y^2)*z^2 == 1, {x, -2, 2}, {y, -3, 3}, {z, 0, 5},PlotRange -> {Automatic, Automatic, {0, 4}} ,RegionFunction -> Function[{x, y, z}, 0 < x^2 + y^2]]
  

• Method 3:

  ParametricPlot3D[{u, v, 1/Sqrt[u^2 + v^2]}, {u, -2, 2}, {v, -2, 2}, Exclusions -> {u^2 + v^2 == 0}, PlotRange -> {Automatic, Automatic, {0, 4}} ]