Message Boards Message Boards

How to avoid road accidents in New York?

In 2014 Conrad Wolfram gave a fascinating TEDx talk. The main question is whether more data has led to better decision making and better democracy. He suggests that there is more and more data, but the data is often not in an accessible form. Certainly, the Wolfram's language curated data is a great resource, but a large number of its features for data processing make it possible to analyse data which originates elsewhere, e.g. from the internet. The drive to make data openly available can be seen everywhere; a great example is the NYC open data initiative. The data might not be in a curated form, but the Wolfram Language allows us to easily work with the data.

I will look at traffic accidents in New York City; here is the data to produce images like this one:

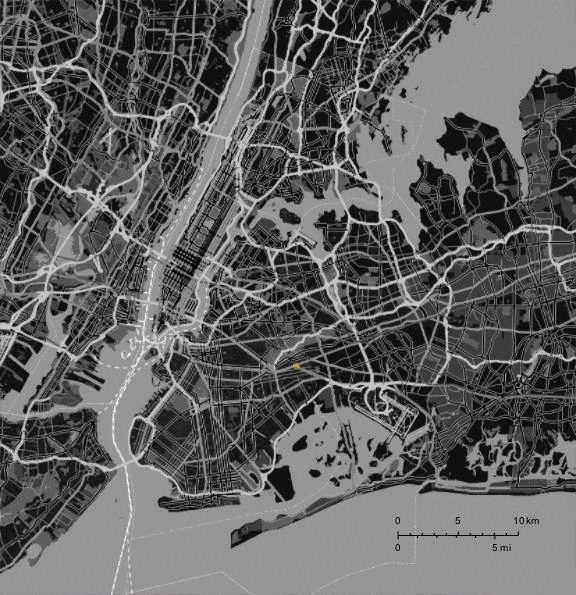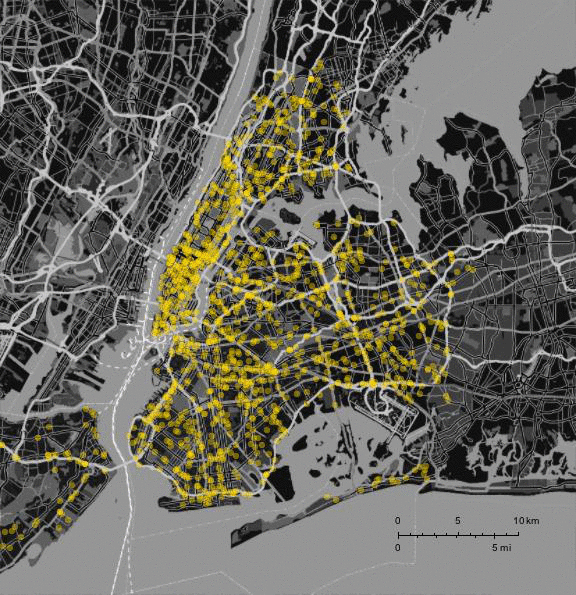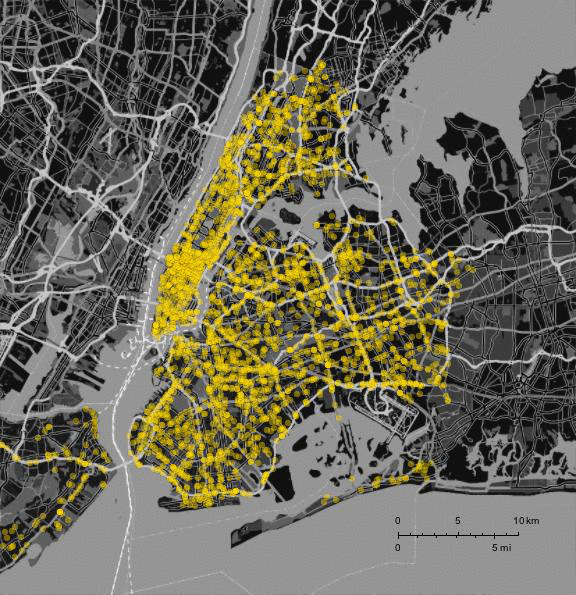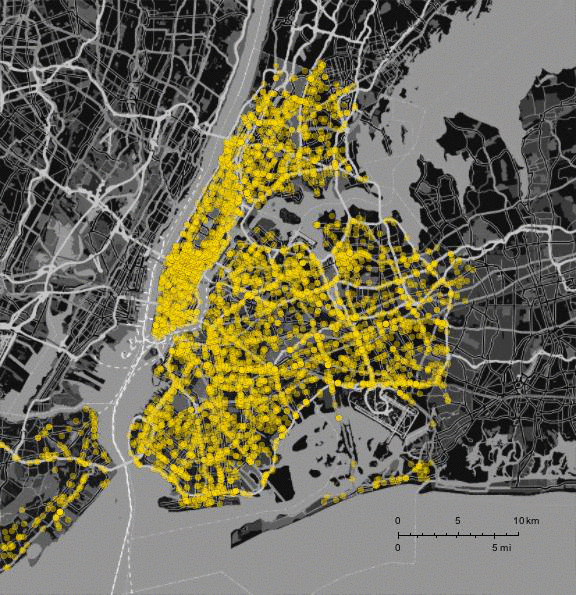
enter image description here

You can export the data in csv format from the website and then import into Mathematica:

data = Import["/Users/thiel/Desktop/NYPD_Motor_Vehicle_Collisions.csv"];

There is an awful lot of information:

data[[1 ;; 5]] // TableForm

enter image description here

These are only the first couple of rows and columns of the data set. This is the content of each of the rows:

data[[1]]

enter image description here

and there are

Length[data]-1

769055 rows with data in it, which we can plot:

styling = {GeoBackground ->GeoStyling["StreetMapNoLabels",GeoStylingImageFunction -> (ImageAdjust@ColorNegate@ColorConvert[#1, "Grayscale"] &)],GeoScaleBar -> Placed[{"Metric", "Imperial"}, {Right, Bottom}],GeoRangePadding -> Full,ImageSize -> Large};
GeoListPlot[GeoPosition /@ DeleteCases[data[[2 ;; 5000, {5, 6}]], {"", ""}], 
 PlotStyle -> Directive[RGBColor[1, 0.85, 0], Opacity[0.4]], styling, GeoRange -> {GeoPosition[{40.50793817653841, -74.16902299250545}, 
"ITRF00"], GeoPosition[{40.95357970888789, -73.59969808862613}, "ITRF00"]}]

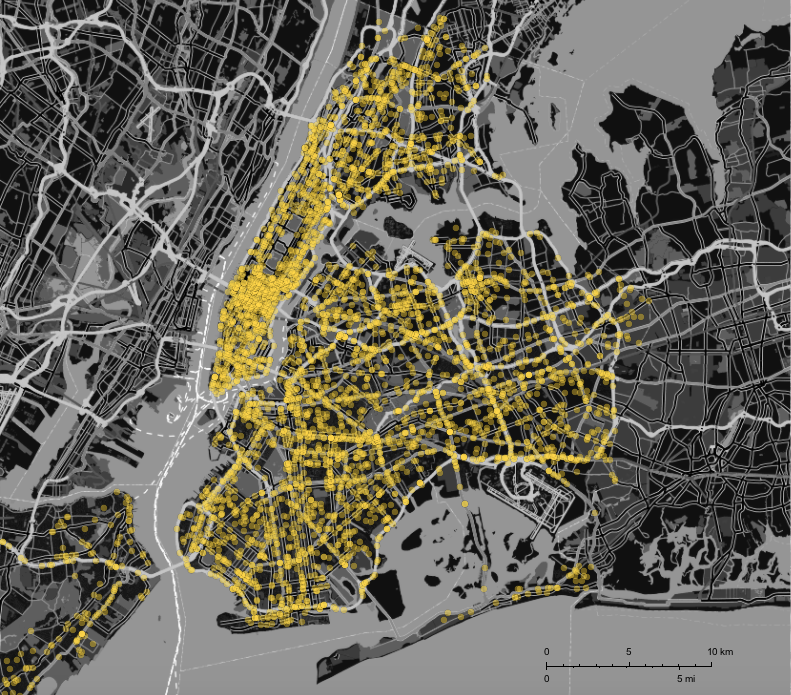
enter image description here

where the styling function is taken from the absolutely outstanding blog post by @Bernat Espigulé Pons on the Runkeeper app: A Year of Runkeeper: Analysis and Visualization. The frames for the movie above were generated using this piece of code:

Monitor[framesaccidents = 
   Table[GeoListPlot[GeoPosition /@ DeleteCases[data[[2 ;; k, {5, 6}]], {"", ""}], PlotStyle -> Directive[RGBColor[1, 0.85, 0], Opacity[0.4]], 
     styling, GeoRange -> {GeoPosition[{40.50793817653841, -74.16902299250545},"ITRF00"], 
       GeoPosition[{40.95357970888789, -73.59969808862613}, "ITRF00"]}], {k, 2, 5002, 100}];, k]

Instead of using ListAnimate I prefer exporting the frames and merging them into a gif in the terminal:

Do[Export["~/Desktop/VehicleCrashes/frame" <> ToString[1000 + k] <> ".jpg", framesaccidents[[k]]], {k, 1, Length[framesaccidents]}]

When do accidents happen?

We can easily extract dates and times from the file and represent when during the day the accidents happen - here for the first 160k accidents in the list:

datestimes = Select[Quiet[DateObject /@ ToExpression[Select[Flatten[StringSplit[#, {"/", ":"}]] & /@ 
        data[[2 ;; 160000, {1, 2}]], Length[#] == 5 &]]], Head[#] == DateObject &];

We can then plot a histogram of that:

Histogram[N@UnitConvert[Quantity[#, "Minutes"], "Hours"] & /@ (60*#[[1]] + #[[2]] & /@ SortBy[DateValue[datestimes, {"Hour", "Minute"}], 1]), 60, 
ImageSize -> Large]

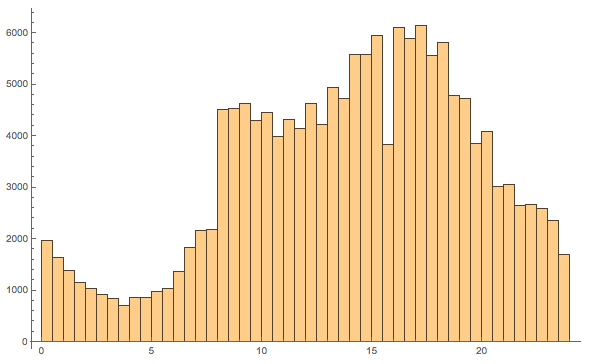
enter image description here

The x-axis show the time of the day and the y-axis the number of accidents. 4 am seems to be a good driving time in New York.

Causes of accidents

The file also contains reasons for the accidents which we can collect like so:

WordCloud[DeleteCases[
   DeleteCases[Flatten[{data[[2 ;; 20000, 19]], data[[2 ;; 20000, 20]]}], "Unspecified"], ""] /. "Driver Inattention/Distraction" -> "Distraction", WordOrientation -> {{-\[Pi]/4, \[Pi]/4}}]

enter image description here

This suggests that it is a good idea not to get distracted when you drive or be too tired.

How many people were injured?

We can also extract information on how many people were injured or killed if any. 

PieChart[{Count[#[[All, 1]], 0], Total[#[[All, 1]] /. "Unspecified" -> 0], Total[#[[All, 2]]] /. "" -> 0} &@ Select[data[[2 ;;]], Length[#] > 11 &][[All, {11, 12}]], 
 ChartLabels -> {"no person injured", "injured", "dead"}, LabelStyle -> Directive[Bold, Medium]]

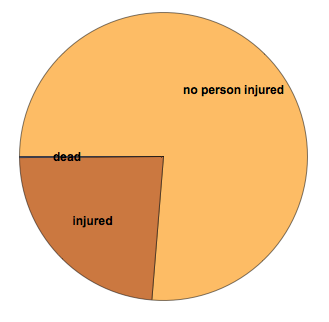
enter image description here

It becomes clear that in most cases nobody gets injured, but there are 980 fatalities listed in the data set.

Which vehicles were involved?

There are conveniently some columns with data to help visualise that.

BarChart[#[[All, 2]], ChartLabels -> Thread@Rotate[#[[All, 1]], Pi/2],LabelStyle -> Directive[Bold, Medium]] & @
Reverse@SortBy[Tally[ToLowerCase /@ DeleteCases[Flatten[Select[data[[2 ;;]], Length[#] > 27 &][[2 ;;, {25, 26, 27, 28}]]], ""]], Last]

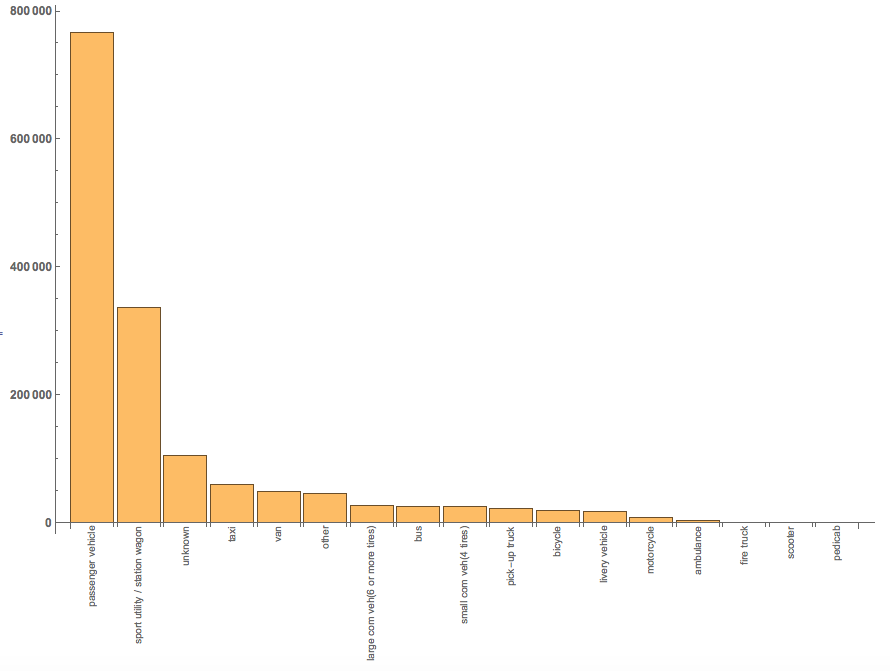
enter image description here

Distribution of accidents

We can now try to estimate the distribution of accidents in New York. The method is motivated by this fantastic post by Michael Trott. 

crashDensityDistribution = SmoothKernelDistribution[RandomChoice[DeleteCases[data[[2 ;; 10000, {5, 6}]], {"", ""}], 2000], "SheatherJones"];
cplot = ContourPlot[PDF[crashDensityDistribution, {y, x}], 
Evaluate@Flatten[{x, {#[[1, 1, 2]], #[[2, 1, 2]]} &@GeoBoundingBox[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]]}], 
Evaluate@Flatten[{y, {#[[1, 1, 1]], #[[2, 1, 1]]} &@GeoBoundingBox[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]]}], 
ColorFunction -> "Rainbow", Frame -> False, PlotRange -> All, Contours -> 405, MaxRecursion -> 2, ColorFunction -> ColorData["TemperatureMap"], 
PlotRangePadding -> 0, ContourStyle -> None, ImageSize -> Full];
GeoGraphics[{Opacity[0.5], GeoStyling[{"GeoImage", cplot}], Polygon[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]]}, GeoRange -> Entity["City", {"NewYork", "NewYork", "UnitedStates"}], ImageSize -> Full]

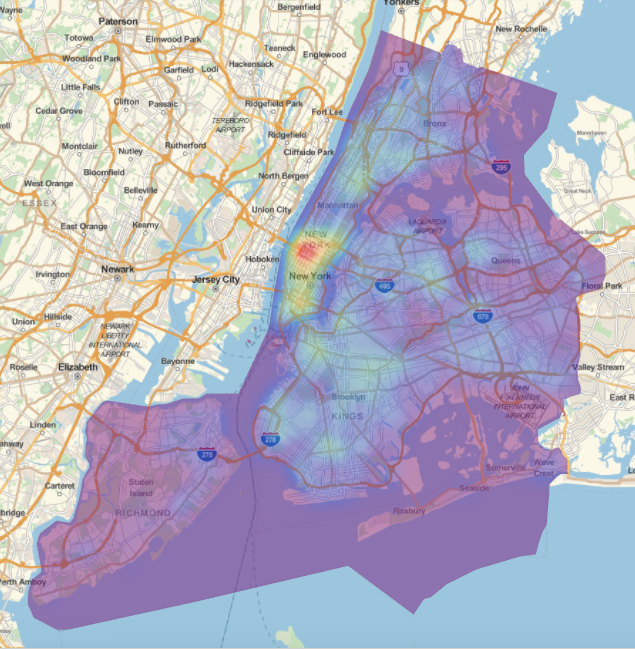
enter image description here

The red area in Manhattan, shows that there is a hot spot. We can add some locations of accidents to help interpret the data:

GeoGraphics[{Opacity[0.5], GeoStyling[{"GeoImage", cplot}], 
Polygon[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]], Black, Opacity[1], PointSize[0.005], 
Point[Reverse /@ RandomChoice[DeleteCases[data[[2 ;; 2000, {5, 6}]], {"", ""}], 1500]]}, 
GeoRange -> Entity["City", {"NewYork", "NewYork", "UnitedStates"}], ImageSize -> Full]

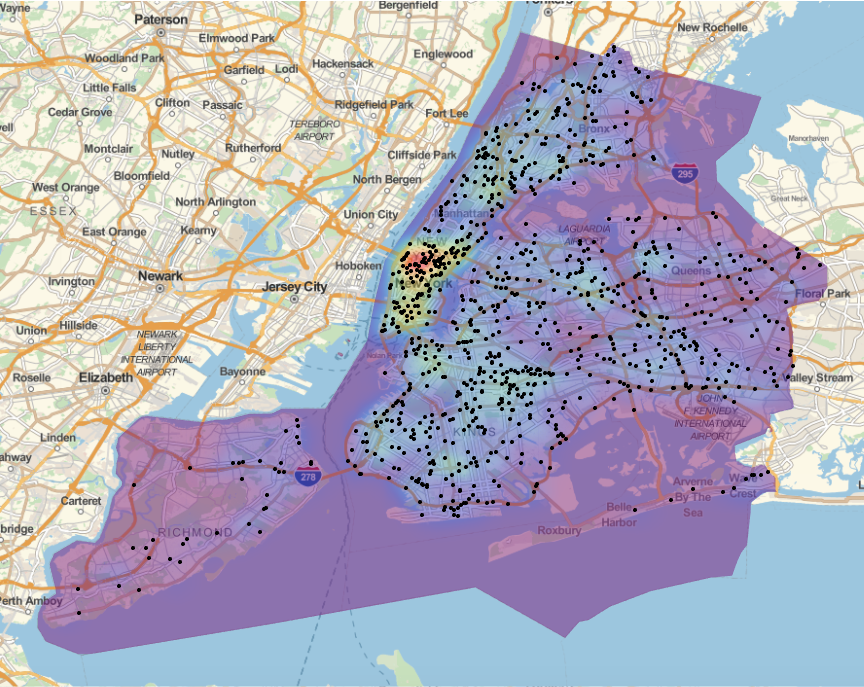
enter image description here

As I said above, I really like @Bernat Espigulé Pons's styling:

GeoGraphics[{Opacity[0.6], GeoStyling[{"GeoImage", cplot}], Polygon[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]], 
Yellow, Opacity[0.2], PointSize[0.005], Point[Reverse /@ RandomChoice[DeleteCases[data[[2 ;; 2000, {5, 6}]], {"", ""}], 1500]]}, 
GeoRange -> Entity["City", {"NewYork", "NewYork", "UnitedStates"}], ImageSize -> Full, styling]

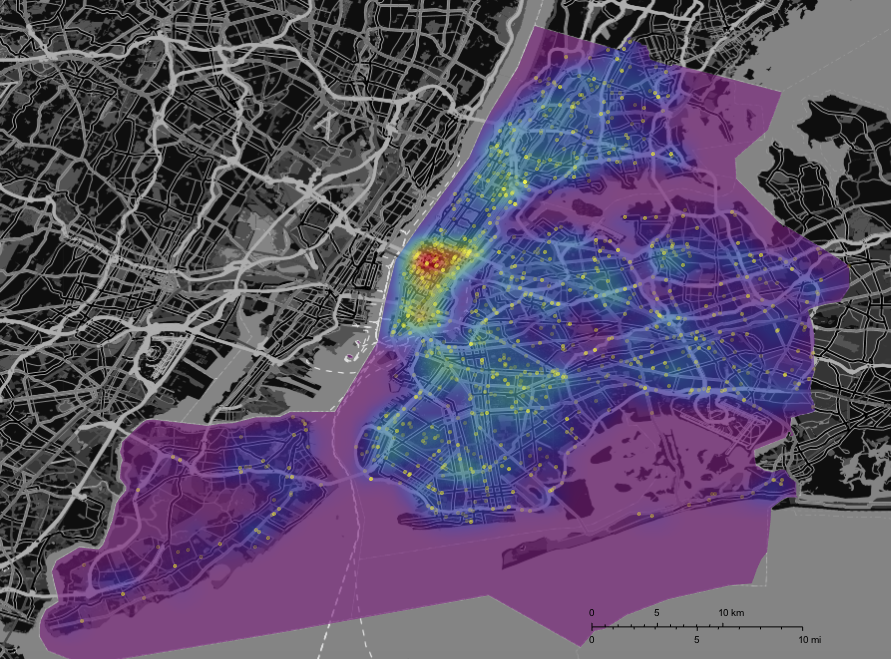
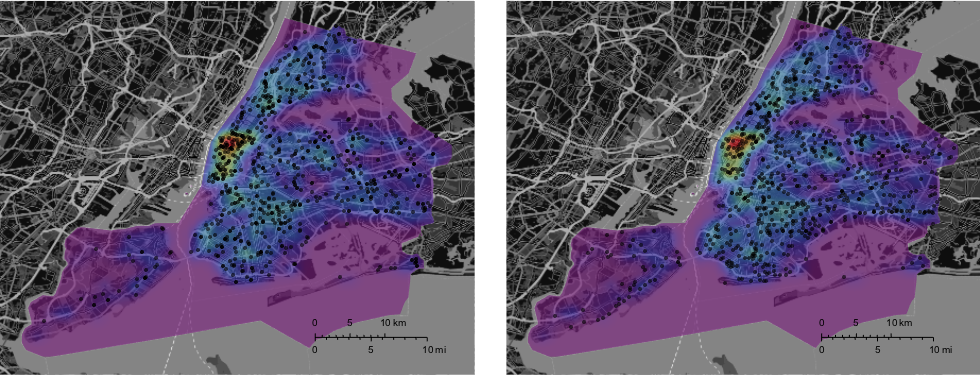
enter image description here

Again we see a strong cluster of accidents in Manhattan. In Central Park there are very few accidents. ;-) We can also represent the deadly accidents as points - where I leave the background distribution of all accidents in place.

GeoGraphics[{Opacity[0.6], GeoStyling[{"GeoImage", cplot}], Polygon[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]], 
Red, Opacity[0.6], PointSize[0.005], Point[Reverse /@ DeleteCases[Select[Select[data, Length[#] > 11 &], #[[12]] > 0 &][[2 ;;, {5, 6}]], {"", ""}]]}, 
GeoRange -> Entity["City", {"NewYork", "NewYork", "UnitedStates"}], ImageSize -> Full, styling]

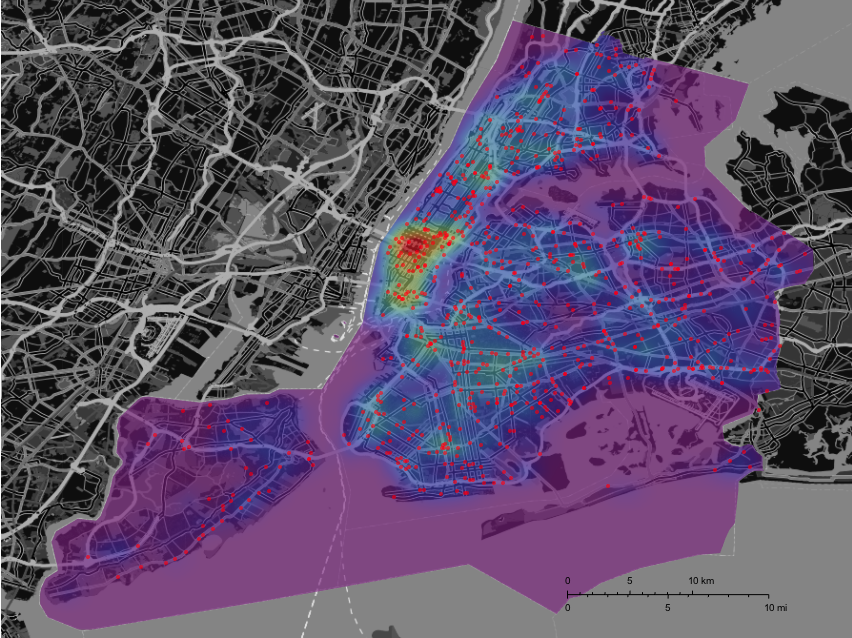
enter image description here

I think that the deadly accidents are slightly less concentrated in Manhattan. We might want to use a hypothesis test to check that. Here are both plots (on the same background) next to each other:

GraphicsRow[{GeoGraphics[{Opacity[0.6], GeoStyling[{"GeoImage", cplot}], 
Polygon[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]], Black, Opacity[0.6], PointSize[0.01], 
Point[Reverse /@ RandomChoice[DeleteCases[data[[2 ;; 2000, {5, 6}]], {"", ""}], 784]]}, GeoRange -> Entity["City", {"NewYork", "NewYork", "UnitedStates"}], ImageSize -> Full, styling], 
GeoGraphics[{Opacity[0.6], GeoStyling[{"GeoImage", cplot}], Polygon[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]], 
Black, Opacity[0.6], PointSize[0.01], Point[Reverse /@ DeleteCases[Select[Select[data, Length[#] > 11 &], #[[12]] > 0 &][[2 ;;, {5, 6}]], {"", ""}]]}, GeoRange -> Entity["City", {"NewYork", "NewYork", "UnitedStates"}], ImageSize -> Full, styling]}]

enter image description here

Let's adapt the distribution function for the deadly accidents and plot it again:

crashDensityDistributiondeadly = SmoothKernelDistribution[
   DeleteCases[Select[Select[data, Length[#] > 11 &], #[[12]] > 0 &][[2 ;;, {5, 6}]], {"", ""}], "SheatherJones"];
cplotdeadly = ContourPlot[PDF[crashDensityDistributiondeadly, {y, x}], 
Evaluate@Flatten[{x, {#[[1, 1, 2]], #[[2, 1, 2]]} &@GeoBoundingBox[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]]}], 
Evaluate@Flatten[{y, {#[[1, 1, 1]], #[[2, 1, 1]]} &@GeoBoundingBox[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]]}], 
ColorFunction -> "Rainbow", Frame -> False, PlotRange -> All, Contours -> 405, MaxRecursion -> 2, ColorFunction -> ColorData["TemperatureMap"], 
PlotRangePadding -> 0, ContourStyle -> None, ImageSize -> Full];
GraphicsRow[{GeoGraphics[{Opacity[0.6], GeoStyling[{"GeoImage", cplot}], Polygon[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]], 
Black, Opacity[0.6], PointSize[0.01], Point[Reverse /@ RandomChoice[DeleteCases[data[[2 ;; 2000, {5, 6}]], {"", ""}], 784]]}, 
GeoRange -> Entity["City", {"NewYork", "NewYork", "UnitedStates"}],ImageSize -> Full, styling], 
GeoGraphics[{Opacity[0.6], GeoStyling[{"GeoImage", cplotdeadly}], Polygon[Entity["City", {"NewYork", "NewYork", "UnitedStates"}]], 
Black, Opacity[0.6], PointSize[0.01], Point[Reverse /@ DeleteCases[Select[Select[data, Length[#] > 11 &], #[[12]] > 0 &][[2 ;;, {5, 6}]], {"", ""}]]}, GeoRange -> Entity["City", {"NewYork", "NewYork", "UnitedStates"}], ImageSize -> Full, styling]}]

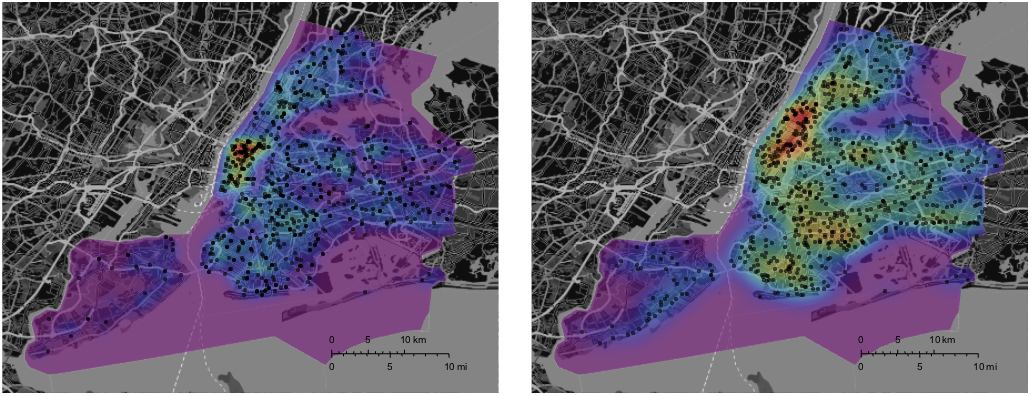
enter image description here

Mathematica has obviously adjusted the colour scale, but it becomes quite clear that deadly accidents seem to be more "spread out" than all accidents. This is an oversimplification, but it suggests that you are more likely to be caught in an accident in Manhattan, but you are more likely to survive it.

This is only the very first bit of the analysis and we have not explored many interesting bits of information hidden in the dataset. One thing that would be nice is to modify TravelDirections as to take into consideration that certain streets/regions are more dangerous.

Cheers,

Marco
POSTED BY: Marco Thiel
5 Replies
Sort By:
Diego Zviovich
Diego Zviovich
Posted 9 years ago

Marco, loved the color palette and the data analysis.

The following is a posting from last year reagarding dangerous intersections in Atlanta.
POSTED BY: Diego Zviovich

Dear Diego,

thanks for the link. I did not remember that post. It is good to see that you get a nearly identical distribution of times of crashes as this data set gets. An interesting question would be: what are the differences, e.g. most accidents happen at crossings, but are the statistically significant differences between NYC and Atlanta in terms of where accidents happen.

It is obvious from your post, and also what we would expect, that larger crossings with more people passing have a higher accident rate. I thought about combining this with TravelDirections, similar to Bernat's post or Sander's. One would have to look at paths between any (or as many as possible) pairs of points and see which roads/crossings are taken most frequently. Of course, observed/measured traffic flow data might even be better.

Thanks,

Marco

PS: Are you aware of any other cities in the US that have similar data sets?

POSTED BY: Marco Thiel

Marco, thanks a lot for sharing these stunning visualizations! That's really interesting but tragic data:

data = SemanticImport["https://data.cityofnewyork.us/api/views/h9gi-nx95/rows.csv?accessType=DOWNLOAD"]

dataset

Turning this data into a Wolfram Language Dataset makes it handy:

DateListPlot[Counts[data[All, "TIME"]], ColorFunction -> "TemperatureMap", PlotRange -> {All, 3000}]

DateListPlot average day

datadays = Counts /@ Sort@GroupBy[data[All, {DateValue[#DATE, "DayName"], Round[AbsoluteTime[#TIME], 15*60]} &], First][All, All, 2]

data days

DateListPlot[datadays, PlotLegends -> Normal@Keys[datadays], 
FrameTicks -> {TimeObject /@ Range[0, 24, 2], Automatic}, PlotTheme -> "Marketing", ImageSize -> 600]

data
POSTED BY: Bernat Espigulé

Dear Bernat,

thanks a lot - in fact the stunning part of the visualisations comes from your post and from Michael Trott's post. You have a really impressive way of creating spectacular graphics. I was merely trying to mimic that.

Yes, the dataset structure is nice and elegant. Your graphic clearly shows the difference between weekdays and weekends. There are also the hourly peaks which appear to be an artefact of the recording of accidents. People/police appear to be using full (or half) hours when they record a crash. I saw that effect, too, and tried to get the curve relatively smooth by choosing the bins accordingly.

Also you are quite right when you say that the data is very tragic. On that website there are lots of other data sets, some of which are really interesting. I wish there was more of that here in the UK.

I am also thinking in the direction that Conrad Wolfram was pointing at. What if more data is made publicly available? Will that further democracy and decision making? I'd love to see what can be learnt from combining different data sets. Is the total more than the sum of its parts? I guess that many of the individual entities that provided data will not be looking at all the other data sets. The Wolfram Language should be really convenient to achieve just that.

For example, I don't think that they have lots of roundabouts there, but it would be interesting to see how accidents/crashes relate to different types of road crossings for example. Or the Tree Census Data; one could also use netatmo data for example.

I think that the datasets on that website are quite amazing.

Thanks a lot for leaving a message!

Marco
POSTED BY: Marco Thiel

enter image description here - another post of yours has been selected for the Staff Picks group, congratulations !

We are happy to see you at the tops of the "Featured Contributor" board. Thank you for your wonderful contributions, and please keep them coming!
POSTED BY: EDITORIAL BOARD
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract