After much consideration, I have divided what was intended as one post into two. The first part is a description of programming the game Minesweeper and ultimately deploying it as a CDF. Concepts from this post are continued in part two which explores the methodology used in creating hexagonal minesweeper and how these techniques can be adapted for methods of pathfinding.

I learnt not only WL but programming in general by doing projects like this below so this step-by-step format is a homage to that experience while also hopefully being of benefit to anyone who is starting out and would like to learn programming while having fun.

The chronology of this project is as follows: A while back, I made a rudimentary version of the classic game Minesweeper.

!

All the basic elements were there but it lacked nearly all of the features needed to make it playable in a realistic setting ( such as automated uncovering of empty tiles) and toggling between uncover and flag was a nuisance. Perhaps the biggest drawback however was the idea of generating a UI via displaying buttons in array form and it became clear that I was quickly coding myself into more problems. The project was shelved but the notion of returning to it with a better approach and developed skills was always in my mind.

Recently having blown off the dust from the project, I wanted a change of scene to keep it interesting so I immediately began work on hexagonal minesweeper.

Probably not the best approach to solving the problems of the original version but it took me on a pretty interesting journey and by contrast, classic minesweeper became a nearly trivial task.

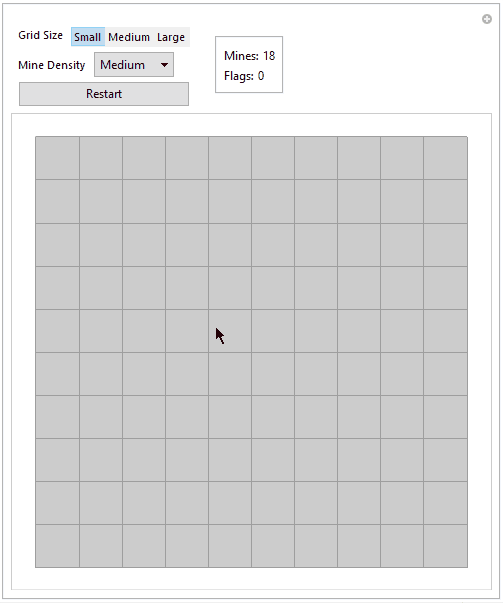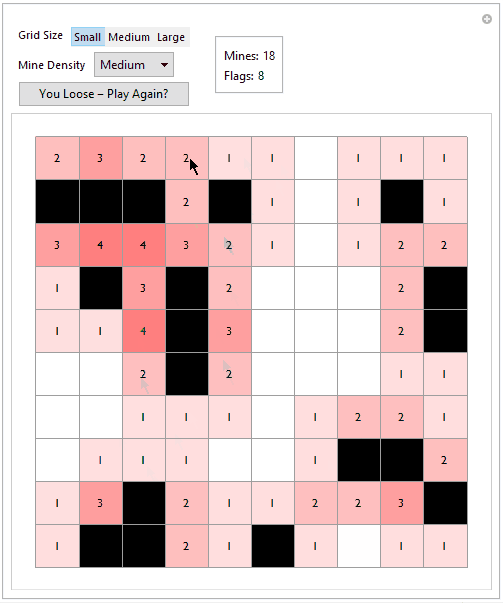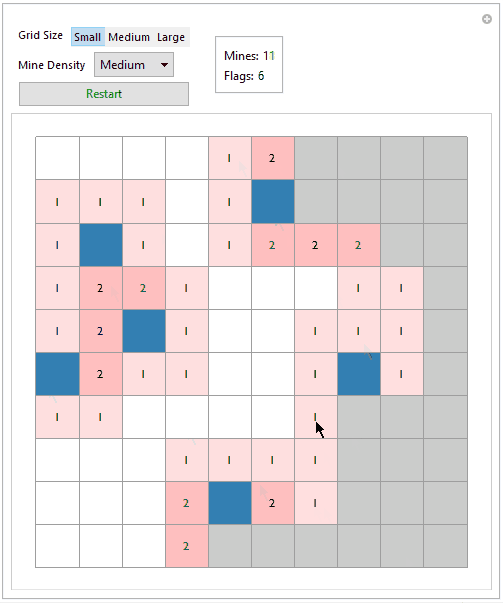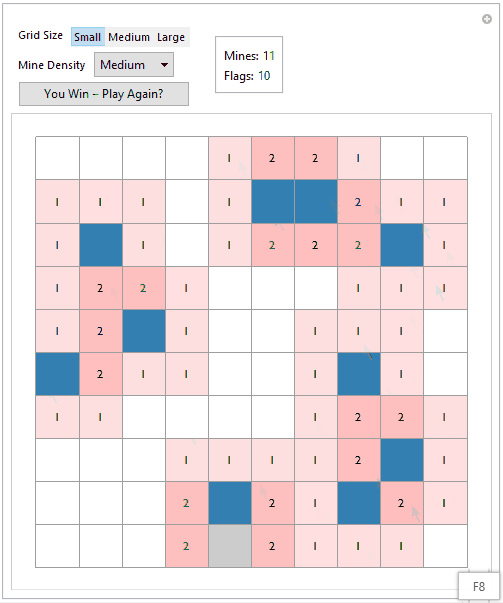
However, things got really interesting when I was testing the chain uncover feature.

This made me think of videos demonstrating pathfinding algorithms. With classic minesweeper being pretty much completed and hex minesweeper still remaining as a functional prototype, the project shifted into a new direction. But first we go back to the start and describe the implementation of classic minesweeper.

Classic Minesweeper

The rules and description of the game can be found here: http://windows.microsoft.com/en-us/windows/minesweeper-how-to#1TC=windows-7

Step 1

We define a function which generates a square array of side-length given by the variable gridLength. Each entry in the array has a probability of mineProb of being a mine (expressed as "m"), otherwise, the array entry is blank (0).

grid = RandomChoice[{#1, 1 - #1} -> {"m", 0}, {#2, #2}] &;

(* probability that location is a mine *)
mineProb = 0.1;

(* side-length of grid *)
gridLength = 10;

A simple approach but the number of mines for any game is variable to within a certain range (unlike official minesweeper where its always a set value).

Step 2

We need the (array) locations of mines and safe (not mines) tiles.

safe =(*array positions of safe tiles*)Position[test, 0]
mines =(*array positions of mine tiles*)Position[test, "m"]

This outputs

Step 3

We need to calculate the number of mines adjacent to each safe tile so we can generate the tile-tips which allow the user to play the game correctly.

Define a function which returns the location of all nearest neighbours (NNs) for a given tile with location {x,y}. On a square tessellation, finding nearest neighbours is simple.

(* NNs of given location *)
nn = Select[0 < #[[1]] <= gridLength &]@

Select[0 < #[[2]] <= gridLength &]@{ {#1 - 1, #2 + 1}, {#1 , #2 + 1}, {#1 + 1, #2 + 1}, {#1 - 1, #2}, {#1, #2}, {#1+1, #2}, {#1 + 1, #2 - 1}, {#1, #2 - 1}, {#1 + 1, #2 - 1} } &;

Included are cases to ignore results given when finding NNs from the grid boundary since some will be out of range. For instance, location {1,1} has NNs {{2,0},{1,0},{0,,0},{0,1},{0,2}} which are all out of bounds (0 < gridLength ). Similarly, any NN location containing a value greater than the array length is also invalid.

Now we use the NN function to calculate the number of mines adjacent to each safe tile.

(* number of NNs which are mines for each safe location *)
mineCount = 
 Table[Length[
      Flatten[Intersection[nn[First@safe[[#]], Last@safe[[#]]], 
        mines]]]/2 &[i], {i, 1, Length[safe]}]

{1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 2, 2, 
1, 0, 0, 0, 1, 1, 0, 2, 2, 1, 1, 1, 0, 1, 0, 2, 2, 1, 2, 1, 1, 1, 0, 
1, 1, 1, 2, 2, 3, 1, 1, 0, 0, 1, 1, 2, 2, 1, 1, 0, 0, 1, 3, 2, 1, 0, 
1, 1, 0, 0, 1, 2, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0}

This reads as the 1st safe location has a total of 1 adjacent mine, the 3rd has 0 adjacent mines, and so on ..

Step 4

Now we insert the tile-tips into the game grid.

new =(*insert nn mine count*)
 ReplacePart[test, 
  Table[safe[[i]] -> mineCount[[i]], {i, 1, Length[safe]}]]

{{1, "m", 1, 0, 1, 1, 1, 1, "m", 1}, {1, 1, 1, 0, 1, "m", 1, 1, 1, 
  1}, {0, 0, 0, 1, 2, 2, 1, 0, 0, 0}, {1, 1, 0, 2, "m", 2, 1, 1, 1, 
  0}, {"m", 1, 0, 2, "m", 2, 1, "m", 2, 1}, {1, 1, 0, 1, 1, 1, 2, 2, 
  3, "m"}, {1, 1, 0, 0, 1, 1, 2, "m", 2, 1}, {"m", 1, 0, 0, 1, "m", 3,
   2, 1, 0}, {1, 1, 0, 0, 1, 2, "m", 1, 0, 0}, {0, 0, 0, 0, 0, 1, 1, 
  1, 0, 0}}

Viewed using Grid[]

Its starting to look like minesweeper!

Step 5

The game interface is an array plot of the data which we've generated, however, it also needs to be 'masked' as to appear like an uncovered tile. There are two arrays of data: the game data which we've just generated and the array which the user sees via ArrayPlot[].

 (*Generate interface - this is what the user will see ("U" for Uncovered) *)
show = ConstantArray["U", Dimensions[new]]

 {
 {"U", "U", "U", "U", "U", "U", "U", "U", "U", "U"},
 {"U", "U", "U", "U", "U", "U", "U", "U", "U", "U"}, 
 {"U", "U", "U", "U", "U", "U", "U", "U", "U", "U"},
 {"U", "U", "U", "U", "U", "U", "U", "U", "U", "U"},
 {"U", "U", "U", "U", "U", "U", "U", "U", "U", "U"},
 {"U", "U", "U", "U", "U", "U", "U", "U", "U", "U"}, 
 {"U", "U", "U", "U", "U", "U", "U", "U", "U", "U"},
 {"U", "U", "U", "U", "U", "U", "U", "U", "U", "U"}, 
 {"U", "U", "U", "U", "U", "U", "U", "U", "U", "U"}, 
 {"U", "U", "U", "U", "U", "U", "U", "U", "U", "U"}
}

While tiles are uncovered during gameplay, the show array will be updated by replacement with it's corresponding (by array location) values in the new array.

Step 6

We use Inset[] to plot the tile-tips over the array plot at the central location of each tile. However, Inset[] uses image coordinates which originate from the bottom-left (and also start at 0) of the array plot while the array locations (which start at 1) have their origin at the top-left. (We could change it so that the array locations begin at 0 but this would only solve half of the problem).

(* Generate list of tip value and plot location *)
(* `Inset` uses image coordinates while the grid uses array coordinates - they arent the same! *)

(* plot location of tip corresponding to array location of associated array entry *)
index = Flatten[
  Table[{j, i}, {i, gridLength, 1, -1}, {j, 1, gridLength, 1}], 1]

{{1, 10}, {2, 10}, {3, 10}, {4, 10}, {5, 10}, {6, 10}, {7, 10}, {8,10}, {9, 10}, {10, 10},
 {1, 9}, {2, 9}, {3, 9}, {4, 9}, {5, 9}, {6,9}, {7, 9}, {8, 9}, {9, 9}, {10, 9}, 
{1, 8}, {2, 8}, {3, 8}, {4,8}, {5, 8}, {6, 8}, {7, 8}, {8, 8}, {9, 8}, {10, 8},... 
{1, 1}, {2, 1}, {3, 1}, {4, 1}, {5, 1}, {6,1}, {7, 1}, {8, 1}, {9, 1}, {10, 1}}

So the 1st tile with array location {1,1} has image coordinate {1,10} and so on.. Well, nearly. I said we want the central location so that the tips appear in the centre of each tile. Each tile has side length of 1, so we simply subtract 0.5 from each coordinate.

(* Use to label array plot with tile tips *)  
tips = Table[
  Inset[(Style[#, Black, 12, "Title"] & /@ 
      ToString /@ (Flatten[new] /. {0 -> ""}))[[i]], 
   index[[i]] - 0.5], {i, 1, gridLength^2}]

This generates a list of insets each with a tile-tip outputted as a string (ToString /@...) and its adjusted plot coordinate.
Style[#, Black, 12, "Title"] & /@ maps over each tile-tip string and styles it accordingly (looks nice). Empty (0) tiles have also been replaced with whitespace ("") ((Flatten[new] /. {0 -> ""})) so that only non-zero tile tips are visible.

Step 7

The array plot will present our game as a grid of coloured tiles (with a string overlay for tile-tips). We need to define a colour scheme which looks nice and is intuitive too.

Hue[] takes a value between 0 and 1 to determine colour. Hue[1, 0, 1] returns red with 0 saturation (white) while Hue[1, 1, 1] returns pure red (full sturation). We want the shades of red in between and enough to assign one to each possible NN mine count (max 8 NNs possible for a sqaure).

(*Generate color scheme *)
colRules = Join[
  Normal[AssociationThread[
    Range[8] -> (Rest[(Hue[1, #, 1] & /@ Rescale[Range[9]])])]],
  {"m" -> Hue[1, 1, 0], "U" -> GrayLevel[0.8], 
   "F" -> RGBColor[0.2, 0.5, 0.7]}
  ]

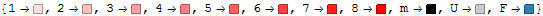
Values for "m", "U" and "F" represent tiles which are mined, uncovered and flagged respectively; these are special cases which we join onto the list of tile-tip colours. I've chosen classic Windows grey as the default tile colour but it can be easily changed to taste.

Step 8

We're now ready to plot the game grid.

We need to be selective at how the tips are inserted

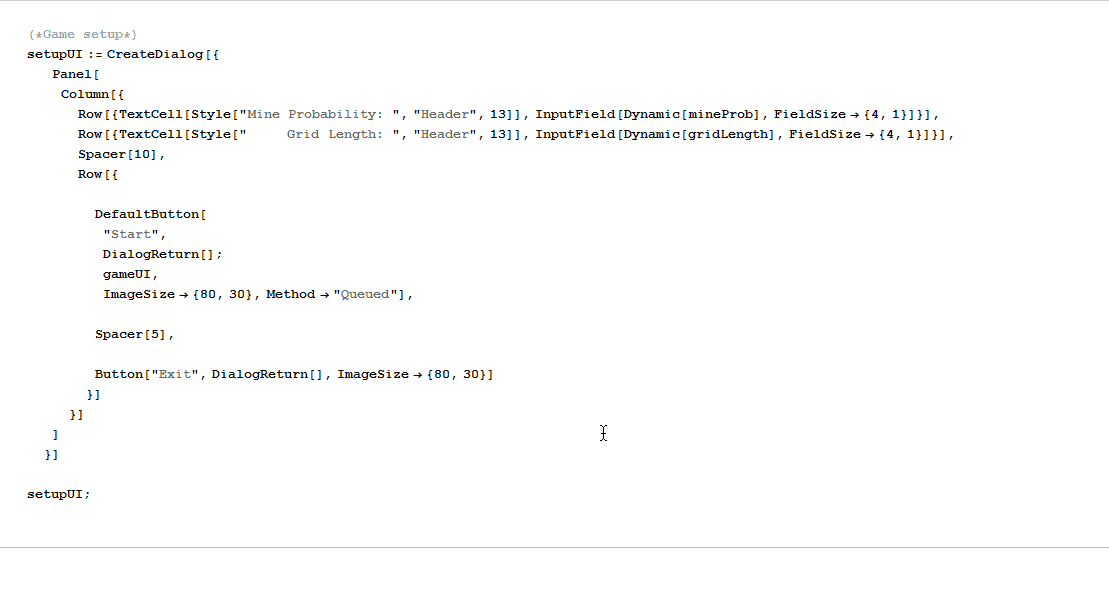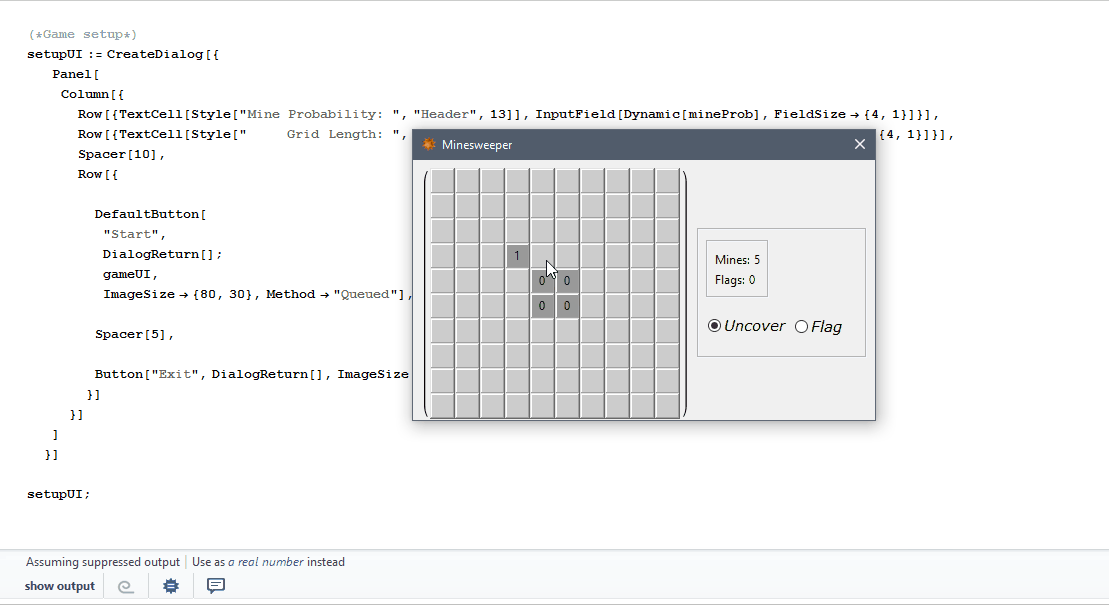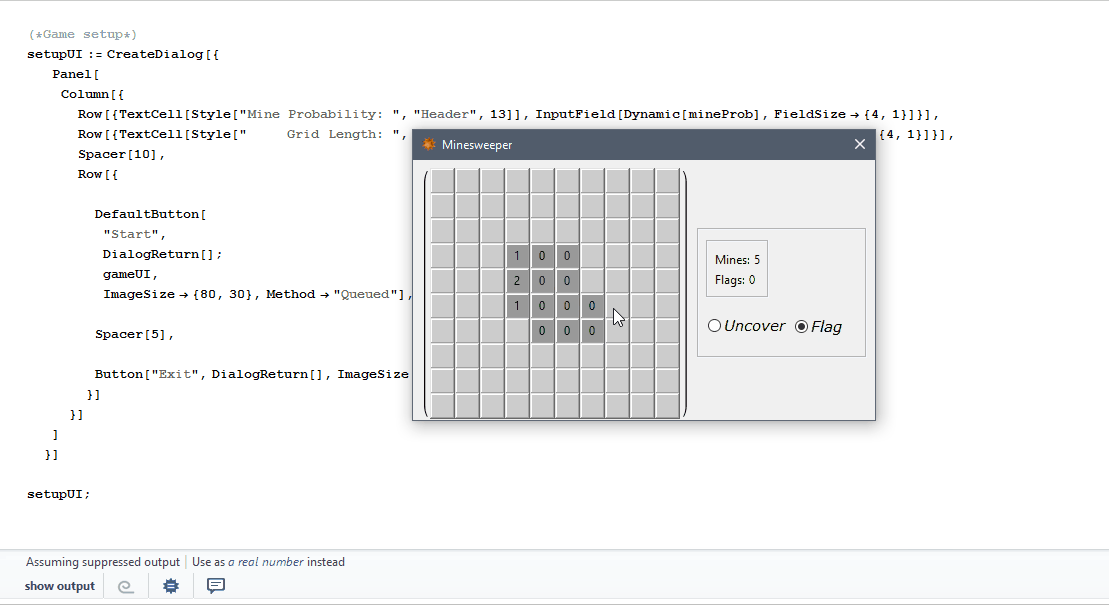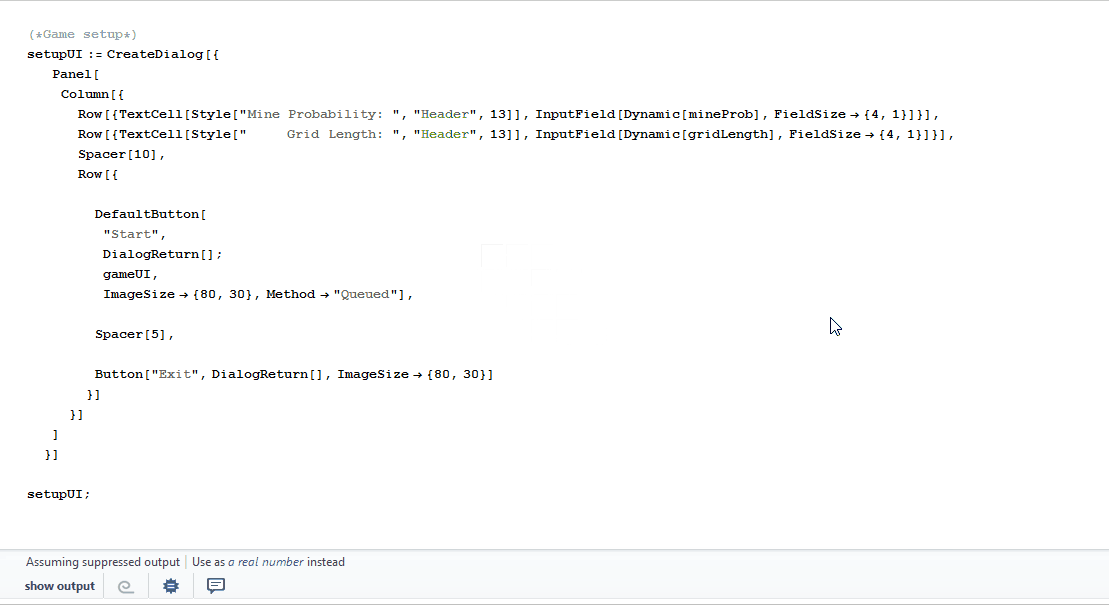
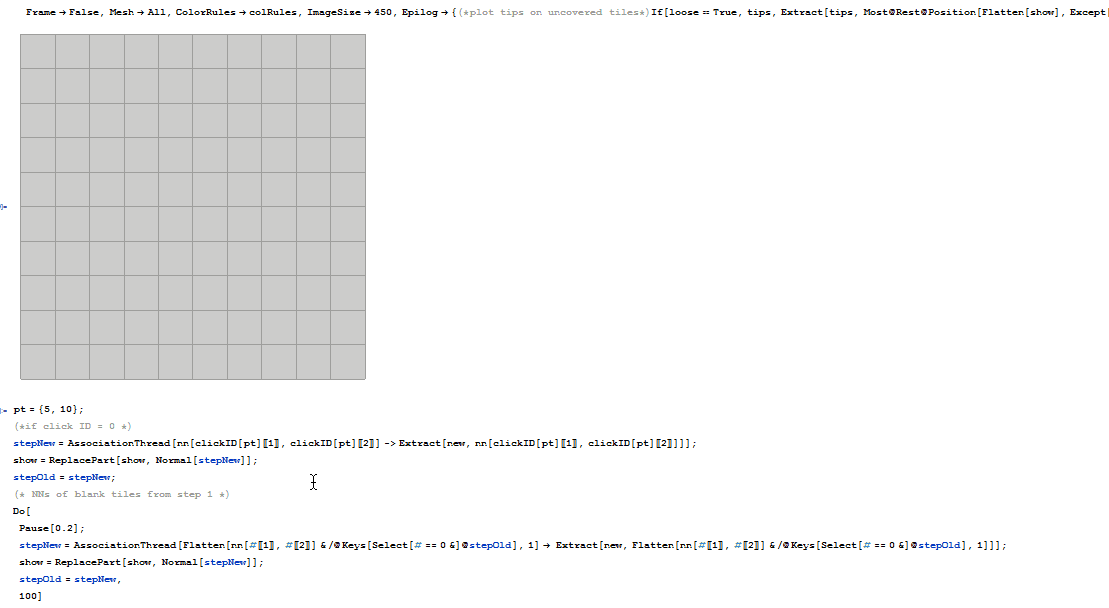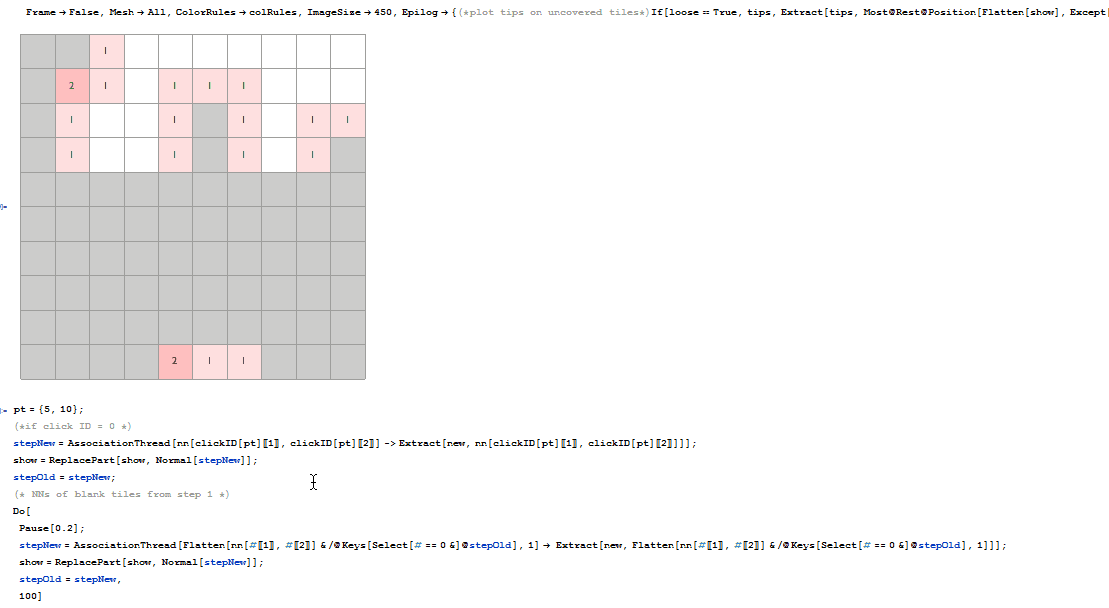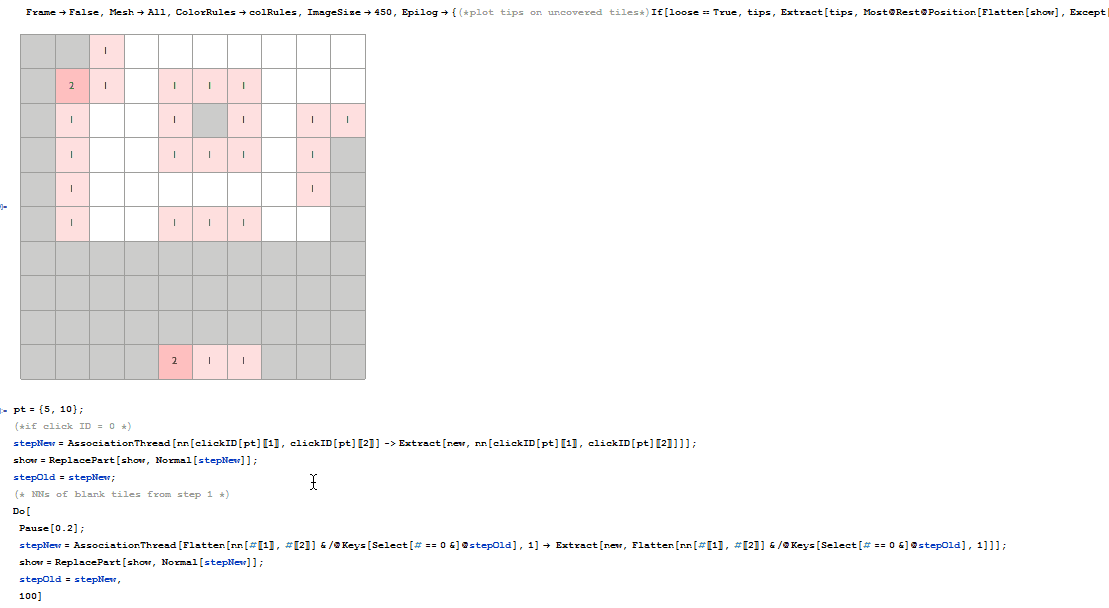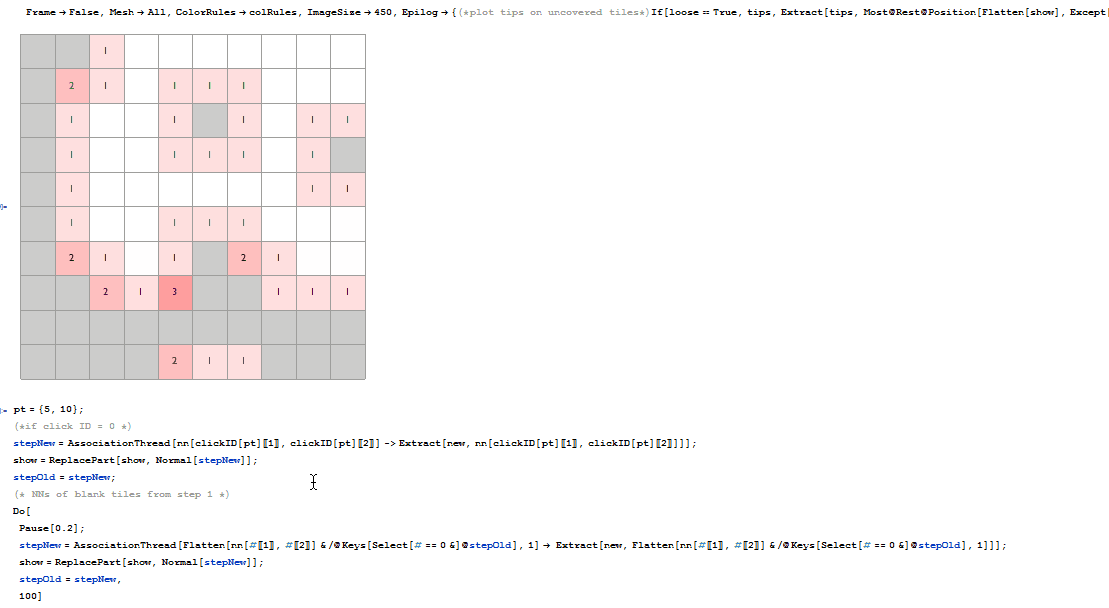
ArrayPlot[
 show,
 Frame -> False, Mesh -> All, ColorRules -> colRules, 
 ImageSize -> 450, Epilog -> {tips}]

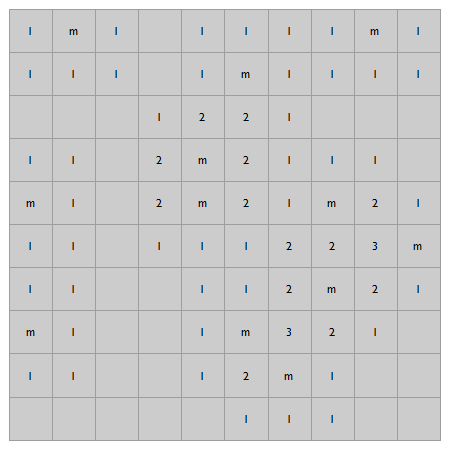
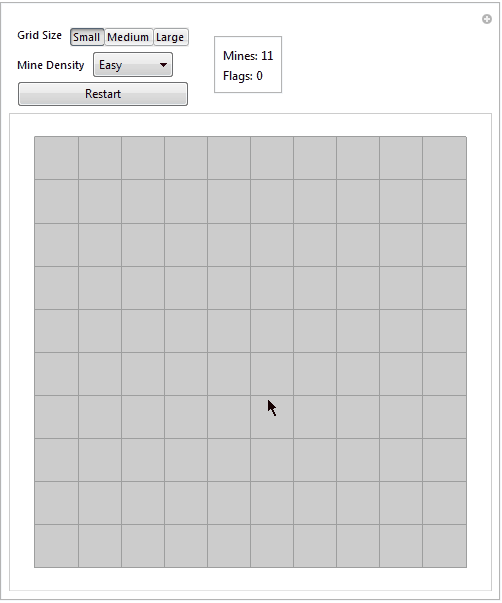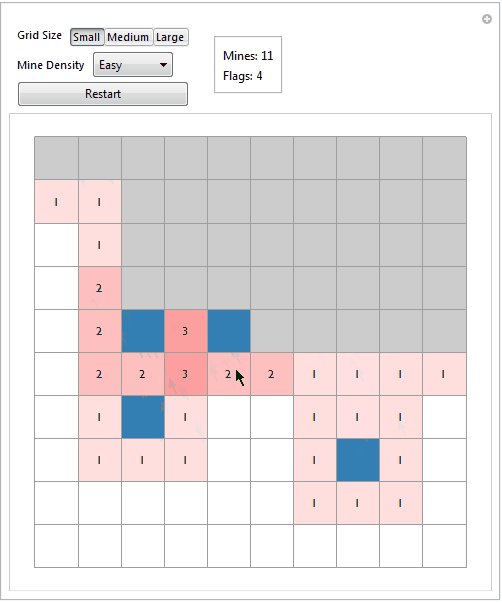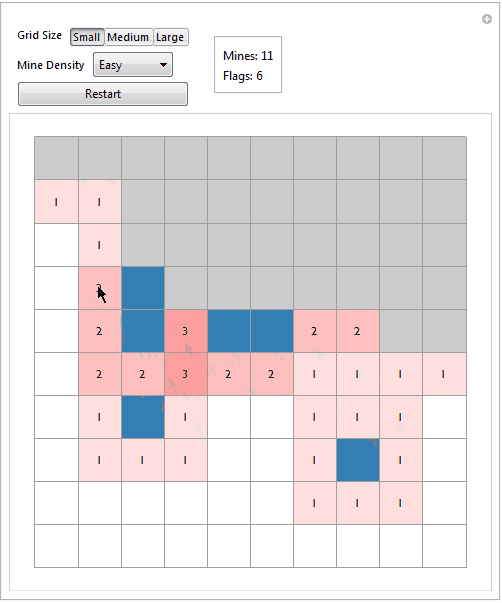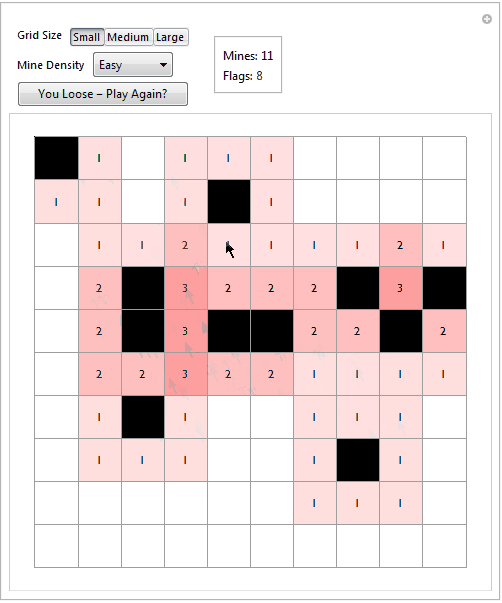
What the player sees at the start of the game.

ArrayPlot[
 show,
 Frame -> False, Mesh -> All, ColorRules -> colRules, 
 ImageSize -> 450, 
 Epilog -> {(*plot tips on uncovered tiles only*)
   Extract[tips, 
    Most@Rest@Position[Flatten[show], Except["U" | "F"]]]}]

What the player sees in a 'loose' condition

ArrayPlot[
 new,
 Frame -> False, Mesh -> All, ColorRules -> colRules, 
 ImageSize -> 450, Epilog -> {tips}]

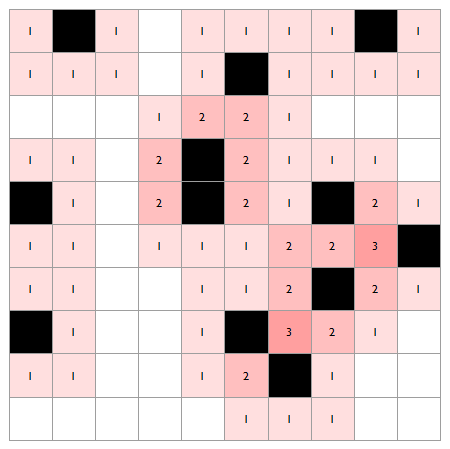
Incorporate both using conditionals.

loose = False;
ArrayPlot[
 Which[
  loose == False, show,
  True, new],
 Frame -> False, Mesh -> All, ColorRules -> colRules, 
 ImageSize -> 450, 
 Epilog -> {(*plot tips on uncovered tiles*)
   If[loose == True, tips, 
    Extract[tips, 
     Most@Rest@Position[Flatten[show], Except["U" | "F"]]]]}]

Step 9

The player will interact with the array plot via mouse clicks, thus we use ClickPane[]. But first we need to readdress the issue of array and image coordinates; same principal as before implemented into a function which takes the click pane mouse coordinates and transforms them into array coordinates.

(* converts rounded ClickPane` output coordinates to array location *)
clickID := {gridLength - #[[2]], 1 + #[[1]]} &;

Wrap ClickPane around the array plot from earlier and introduce a function which rounds the transformed mouse position to the nearest tile location.

ClickPane[
 (* PLOT INTERFACE FROM STEP 8 *)
 ArrayPlot[
  Which[
   loose == False, show,
   True, new],
  Frame -> False, Mesh -> All, ColorRules -> colRules, 
  ImageSize -> 450, 
  Epilog -> {(*plot tips on uncovered tiles*)
    If[loose == True, tips, 
     Extract[tips, 
      Most@Rest@Position[Flatten[show], Except["U" | "F"]]]]}],

 (* MOUSE INTERACTIVE CONTROLS *)

 (* takes click location and rounds to nearest square *)
 (pt = IntegerPart[#];

Then we add the mouse click controllers - this is what we want ClickPane to do in the event of a mouse click.

(* DEFAULT - CLICK TO UNCOVER TILE *)
   If[CurrentValue["ShiftKey"] == False,

     (* 'uncover' tile by replacing the `show` array with its \
corresponding value according to the array compuated in step 3 *)
     show = 
      ReplacePart[show, clickID[pt] -> Extract[new, clickID[pt]]],

     (* OTHERWISE, IF SHIFT KEY IS PRESSED: *)
     (* if ShiftKey is pressed *)
     Which[
      (* toggle flags for covered tiles *) 
      Extract[show, clickID[pt]] == "U", 
      show = ReplacePart[show, clickID[pt] -> "F"],
      Extract[show, clickID[pt]] == "F", 
      show = ReplacePart[show, clickID[pt] -> "U"]
      ]
     ];) &]

We're using the shift key to alternate between uncovering and flagging/un-flagging tiles. (Un)flagging works by changing the tile's array value to ("U") "F".

We have now reached the most basic level of interactivity. Note that there is no enforcement of rules or automation; i.e., chain uncovering of blank tiles, automatic NN uncovering for selected tiles. Hence user needs to click a lot to play and the game quickly becomes tedious (and this is from someone who once lost an entire Sunday from playing Cookie Clicker)

Step 10

Add win loose conditions.

(*win condition *)
(* if all safe tiles have been uncovered and the player has not lost *)
win := Position[show, "U" | "F"] == mines && loose == False;

(* loose conditions *)
(* if the player reveals a mine *)
loose := ContainsAny[Position[show, "m"], mines];

You can find reference to these evaluations in the conditional controlling the array plot.

Step 11

Add automation.

(* to be called if player uncovers an empty tile (without tip) *)
(* [4] *)chainUncover := (
  (*if click ID = 0 *)
  (* [1] *)stepNew = 
   AssociationThread[
    nn[clickID[pt][[1]], clickID[pt][[2]]] -> 
     Extract[new, nn[clickID[pt][[1]], clickID[pt][[2]]]]];
  show = ReplacePart[show, Normal[stepNew]];
  stepOld = stepNew;
  (* NNs of blank tiles from step 1 *)
  (* [3] *)Do[
   (* [2] *)stepNew = 
    AssociationThread[
     Flatten[nn[#[[1]], #[[2]]] & /@ Keys[Select[# == 0 &]@stepOld], 
       1] -> Extract[new, 
       Flatten[nn[#[[1]], #[[2]]] & /@ Keys[Select[# == 0 &]@stepOld],
         1]]];
   show = ReplacePart[show, Normal[stepNew]];
   stepOld = stepNew,
   100]
  )

(1) : Associate NNs of clicked (blank) tile with their tips. Since the uncovered tile is blank, these will always be free of mines.

  stepNew = AssociationThread[
  nn[clickID[pt][[1]], clickID[pt][[2]]] -> 
   Extract[new, nn[clickID[pt][[1]], clickID[pt][[2]]]]]

<|{2, 2} -> 1, {2, 3} -> 1, {2, 4} -> 0, {3, 2} -> 0, {3, 3} -> 
  0, {3, 4} -> 1, {4, 2} -> 1, {4, 3} -> 0, {4, 4} -> 2|>

Hence, these may be uncovered immediately.

show = ReplacePart[show, Normal[stepNew]];

Carry results over to next step.

stepOld = stepNew;

(2): For the NNs from (1), for those which are also blank, get their NNs too.

stepNew = 

AssociationThread[ Flatten[nn[#[[1]], #[[2]]] & /@ Keys[Select[# == 0 &]@stepOld],1] -> Extract[new, Flatten[nn[#[[1]], #[[2]]] & /@ Keys[Select[# == 0 &]@stepOld],1]] ]

<|{1, 3} -> 1, {1, 4} -> 0, {1, 5} -> 1, {2, 3} -> 1, {2, 4} -> 0, {2, 5} -> 1,
 {3, 3} -> 0, {3, 4} -> 1, {3, 5} -> 2, {2, 1} ->  1, {2, 2} -> 1, {3, 1} -> 0, 
 {3, 2} -> 0, {4, 1} -> 1, {4, 2} -> 1, {4, 3} -> 0, {4, 4} -> 2, {5, 2} -> 1,
 {5, 3} -> 0, {5, 4} -> 2|>

Uncover tiles

show = ReplacePart[show, Normal[stepNew]];

Carry results over to next step

stepOld = stepNew;

We can now loop this process

Do[
(* [2] *)stepNew = 
AssociationThread[
Flatten[nn[#[[1]], #[[2]]] & /@ Keys[Select[# == 0 &]@stepOld], 
1] -> Extract[new, 
Flatten[nn[#[[1]], #[[2]]] & /@ Keys[Select[# == 0 &]@stepOld], 
1]]];
show = ReplacePart[show, Normal[stepNew]];
stepOld = stepNew,
100]

Do 100 times is me being lazy as I couldn't find a satisfactory end condition and I was keen to move on with the project.

The entire procedure can be wrapped up as a delayed evaluation (4) and ready to be called in the case of a user clicking on an empty tile.

Step 12

We fit it all together within Manipulate.

This is the game component:

ClickPane[
 ArrayPlot[
  Which[
   loose == False, show,
   True, new],
  Frame -> False, Mesh -> All, ColorRules -> colRules, 
  ImageSize -> 450, 
  Epilog -> {(*plot tips on uncovered tiles*)
    If[loose == True, tips, 
     Extract[tips, 
      Most@Rest@Position[Flatten[show], Except["U" | "F"]]]]}],
 (pt = IntegerPart[#];
   If[CurrentValue["ShiftKey"] == False,
    (* uncover tile *)
    (* if tile is blank *)
    If[Extract[new, clickID[pt]] == 0,
     (* uncover tiles plus NNs.. *)
     chainUncover,
     (* else, uncover tile *)
     show = 
      ReplacePart[show, clickID[pt] -> Extract[new, clickID[pt]]]],
    (* if ShiftKey is pressed *)
    Which[
     (* reveal NNs for uncovered tiles *)
     Extract[show, clickID[pt]] =!= "U" =!= "F", 
     show = ReplacePart[show, Normal[
        AssociationThread[
         Keys[Select[
              AssociationThread[
               nn[clickID[pt][[1]], clickID[pt][[2]]] -> 
                Extract[show, 
                 nn[clickID[pt][[1]], clickID[pt][[2]]]]], #1 == 
                "U" &]] ->
            Extract[new, #] &[
          Keys[Select[
            AssociationThread[
             nn[clickID[pt][[1]], clickID[pt][[2]]] -> 
              Extract[show, 
               nn[clickID[pt][[1]], clickID[pt][[2]]]]], #1 == 
              "U" &]]]]]],
     (* toggle flags for covered tiles *) 
     Extract[show, clickID[pt]] == "U", 
     show = ReplacePart[show, clickID[pt] -> "F"],
     Extract[show, clickID[pt]] == "F", 
     show = ReplacePart[show, clickID[pt] -> "U"]
     ]
    ];) &]

Theres also an added feature for uncovering NNs for uncoverd tiles; useful if you think you've flagged it's adjecent mines and want to clear the board quickly.

These are the manipulate controllers:

Row[{
  Column[{
    (* sets length of grid *)
    Control[{{gridLength, 10, "Grid Size"}, {10 -> "Small", 
       20 -> "Medium", 30 -> "Large"(*,40\[Rule]"X Large"*)}}],

    (* sets probability for mine *)
    Control[{{mineProb, 0.1, "Mine Density"}, {0.05 -> "Beginner", 
       0.1 -> "Easy", 0.15 -> "Medium", 0.25 -> "Hard", 
       0.3 -> "Expert", 0.4 -> "Pro"}}],


    (* Reinitializes game (newGame) under current settings *) 
    Button[Dynamic@
      Which[loose == True, "You Loose - Play Again?", win == True, 
       "You Win - Play Again?", True, "Restart"], newGame]
    }],

  (* reads and displays ammount of mines and flags *)
  Panel[
   Column[{
     Row[{TextCell["Mines: "], Dynamic@Length[mines]}],
     Row[{TextCell["Flags: "], Dynamic@Count[show, "F", 2]}]
     }]
   ]}, Spacer[20]]

Everything needed to create a new game goes here:

newGame := (
  label = "Restart";
  test = grid[mineProb, gridLength];
  safe =(*array positions of safe tiles*)Position[test, 0];
  mines =(*array positions of mine tiles*)Position[test, "m"];
  mineCount =(*number of NNs which are mines*)
   Table[Length[
        Flatten[Intersection[nn[First@safe[[#]], Last@safe[[#]]], 
          mines]]]/2 &[i], {i, 1, Length[safe]}];
  new = Replace[test, 1 -> "m", 2];
  new =(*insert nn mine count*)
   ReplacePart[test, 
    Table[safe[[i]] -> mineCount[[i]], {i, 1, Length[safe]}]];
  show = ConstantArray["U", Dimensions[new]];
  index = 
   Flatten[Table[{j, i}, {i, gridLength, 1, -1}, {j, 1, gridLength, 
      1}], 1];
  tips = Table[
    Inset[(Style[#, Black, 12, "Title"] & /@ 
        ToString /@ (Flatten[new] /. {0 -> ""}))[[i]], 
     index[[i]] - 0.5], {i, 1, gridLength^2}];
  )

Everything needed to run the program goes here:

(* this will be automatically evaluated by Manipulate *) 
Initialization :> (

  (* FUNCTIONS - Once set, they may be called at any time *)
  clickID := {gridLength - #[[2]], 1 + #[[1]]} &;
  chainUncover := (
    (*if click ID = 0 *)
    stepNew = 
     AssociationThread[
      nn[clickID[pt][[1]], clickID[pt][[2]]] -> 
       Extract[new, nn[clickID[pt][[1]], clickID[pt][[2]]]]];
    show = ReplacePart[show, Normal[stepNew]];
    stepOld = stepNew;
    (* NNs of blank tiles from step 1 *)
    Do[
     stepNew = 
      AssociationThread[
       Flatten[nn[#[[1]], #[[2]]] & /@ Keys[Select[# == 0 &]@stepOld],
          1] -> Extract[new, 
         Flatten[nn[#[[1]], #[[2]]] & /@ 
           Keys[Select[# == 0 &]@stepOld], 1]]];
     show = ReplacePart[show, Normal[stepNew]];
     stepOld = stepNew,
     100]
    );

  nn =(*nearest neighbours of nth entry of safe tiles - long version*)
   Select[#[[2]] <= gridLength &]@
         Select[#[[1]] <= gridLength &]@
          DeleteCases[#, {0, Integer_}] &@
       DeleteCases[#, {Integer_, 0}] &@{{#1 - 1, #2 - 1}, {#1 - 
        1, #2}, {#1 - 1, #2 + 1}, {#1, #2 - 1}, {#1, #2}, {#1, #2 + 
        1}, {#1 + 1, #2 - 1}, {#1 + 1, #2}, {#1 + 1, #2 + 1}} &;

  grid =(*generate random starting grid*)
   RandomChoice[{#1, 1 - #1} -> {"m", 0}, {#2, #2}] &;
  colRules = Join[
    Normal[
     AssociationThread[
      Range[8] -> (Rest[(Hue[1, #, 1] & /@ Rescale[Range[9]])])]],
    {"m" -> Hue[1, 1, 0], "U" -> GrayLevel[0.8], 
     "F" -> RGBColor[0.2, 0.5, 0.7]}
    ];

  (*win condition *)
  win := Position[show, "U" | "F"] == mines && loose == False;

  (* loose conditions *)
  loose := ContainsAny[Position[show, "m"], mines];

  (* INITILIZE - 
  Everthything that must be evaluated before the program is used for \
the first time *)

  (* default variables *)
  mineProb = 0.1; gridLength = 10; pt = {0, 0};

  (* our newGame as defined earlier *)
  newGame := (
    label = "Restart";
    test = grid[mineProb, gridLength];
    safe =(*array positions of safe tiles*)Position[test, 0];
    mines =(*array positions of mine tiles*)Position[test, "m"];
    mineCount =(*number of NNs which are mines*)
     Table[Length[
          Flatten[Intersection[nn[First@safe[[#]], Last@safe[[#]]], 
            mines]]]/2 &[i], {i, 1, Length[safe]}];
    new = Replace[test, 1 -> "m", 2];
    new =(*insert nn mine count*)
     ReplacePart[test, 
      Table[safe[[i]] -> mineCount[[i]], {i, 1, Length[safe]}]];
    show = ConstantArray["U", Dimensions[new]];
    index = 
     Flatten[Table[{j, i}, {i, gridLength, 1, -1}, {j, 1, gridLength, 
        1}], 1];
    tips = 
     Table[Inset[(Style[#, Black, 12, "Title"] & /@ 
          ToString /@ (Flatten[new] /. {0 -> ""}))[[i]], 
       index[[i]] - 0.5], {i, 1, gridLength^2}];
    );
  (* then have it evaluate it to make a new (and first) game *)
  newGame;
  )

And that's it. A CDF deployment can be made by either selecting the output cell and using the export wizard (File -> CDF Export -> Standalone.. ) or by evaluating something like this below

CDFDeploy[
 FileNameJoin[{NotebookDirectory[], 
   "MinesweeperClassic"}], minesweeperCDF, WindowSize -> {540, 660}, 
 Method -> "Standalone"] 

The source code and step-by-step breakdown notebooks and the CDF can be found at the end of the post.

Final Remarks

The program works as intended and operates well, both in performance and interface. There is much room for optimization of the existing code however. I intend on eventually returning to the project for a third time to not only optimize the code but to add new features too. I have this idea of combining MousePosition with ScheduledTask to make a mouse logger, generate gameplay logs and use this data to analyse the player's ability to scale the difficulty of the game as it progresses.

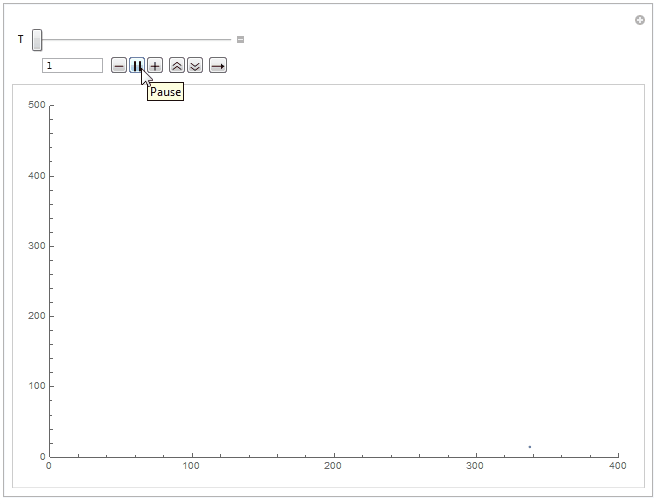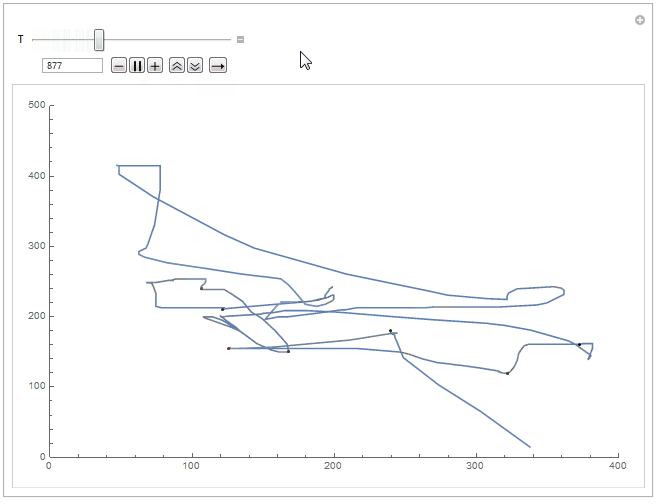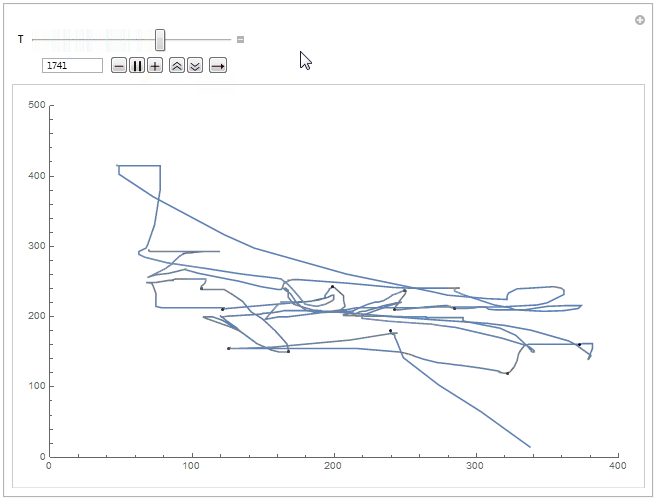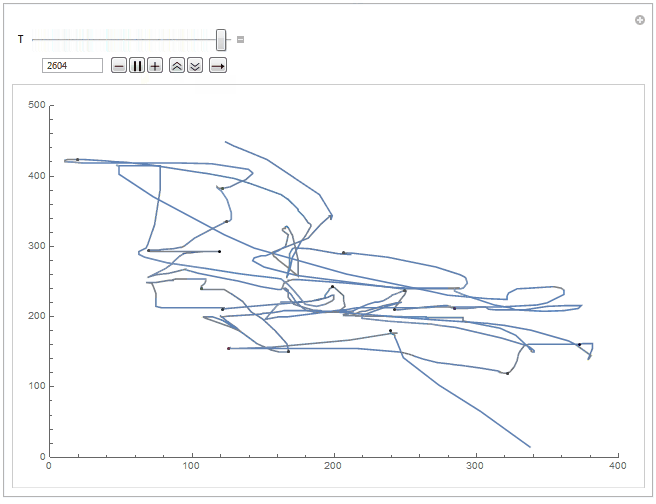
In the meantime though, part two can be read here.

Attachments: