Message Boards Message Boards

Soothing Mandala-like Animation

Life is stressful. Seems unbelievable, but Mathematica can help us relax after just a few lines of code. This quite simple piece of code generates animated mandala-like pictures that will calm you down. At least, this works for me :)

Animate[Graphics@
  Table[{Thick, Dotted, Hue[r/360, 1, 1, .4], 
    Line[{{Cos[x r Degree], Sin[x r Degree]},
             {Cos[39 r Degree], Sin[ 39 r Degree]}}]}, 
  {r, 0, 360, 1}], 
{x,Select[Range[1, 360], ! IntegerQ[#/3] &]}, 
ControlPlacement -> Top,DefaultDuration -> 360]

39 in the second point of line was chosen by chance. I've decided, that 2D parameters are unnecessary. I've also decided to skip multiplies of 3 in iterator x, because they produce not so harmonic pictures as others.

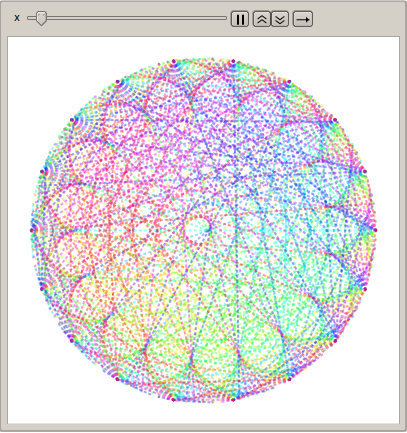
enter image description here

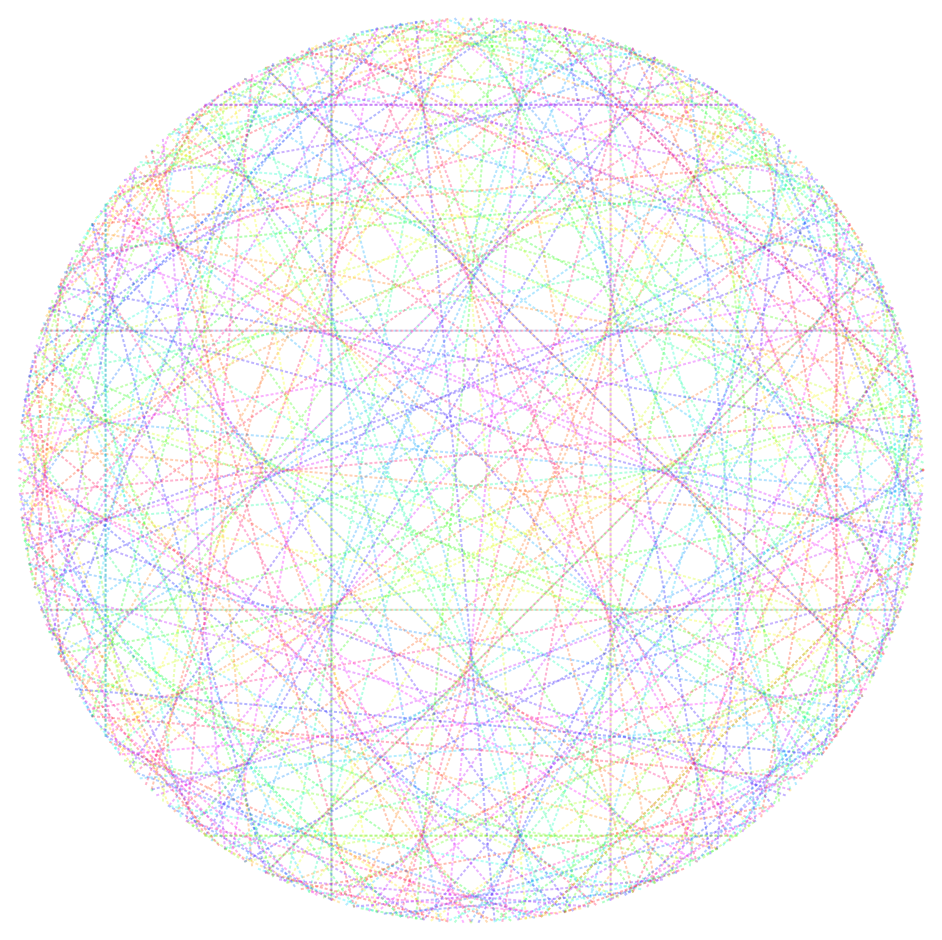
I've also found some images that look especially fascinating for me (however, there is so much more to explore!) enter image description hereenter image description here

So turn on some relaxing music...I hope you'll enjoy it!)
POSTED BY: Dariia Porechna
9 Replies
Sort By:

I am not sure how soothing are these, but I do that find them visually intriguing:

SeedRandom[1587];
ResourceFunction["RandomMandala"]["Radius" -> {10, 11, 9}, 
 "RotationalSymmetryOrder" -> Reverse[11*2^Range[3]], 
 "ConnectingFunction" -> FilledCurve@*BezierCurve, 
 ColorFunction -> "DarkRainbow", FaceForm -> {Opacity[0.3]}, 
 EdgeForm -> {Yellow, Opacity[0.6]}, ImageSize -> 1000]

enter image description here

SeedRandom[2344];
ResourceFunction["RandomMandala"]["Radius" -> {8, 10, 6}, 
 "RotationalSymmetryOrder" -> Reverse[5*2^Range[3]], 
 "ConnectingFunction" -> FilledCurve@*BezierCurve, 
 ColorFunction -> "Rainbow", FaceForm -> {Opacity[0.3]}, 
 EdgeForm -> {Yellow, Opacity[0.6]}, ImageSize -> 1000]

enter image description here
POSTED BY: Anton Antonov

Here are animations based on the random mandalas above:
POSTED BY: Anton Antonov

Wow! This is great material. You can find many of these crazy-looking animations at the Twitter account "Tweet-a-Program": https://twitter.com/wolframtap. Mrs. Silvia Torosyan is a frequent contributor; some of her codes are published thereof. :-)
POSTED BY: Allan Zea

Very nice!
POSTED BY: Clayton Shonkwiler

enter image description here - another post of yours has been selected for the Staff Picks group, congratulations !

We are happy to see you at the tops of the "Featured Contributor" board. Thank you for your wonderful contributions, and please keep them coming!
POSTED BY: EDITORIAL BOARD

If you can generate an animation that makes people dizzy, you could probably make money selling it to people who need to retrain their vestibulo-ocular reflex, the brain circuitry that coordinates inputs from the various senses.

POSTED BY: Frank Kampas

The second one is very neat, can't figure out the 'rule' ! very intricate.
POSTED BY: Sander Huisman

This is it:

Graphics@
  Table[{Thick, Dotted, Hue[r/360, 1, 1, .4], 
    Line[{{Cos[31 r Degree], Sin[31 r Degree]},
             {Cos[39 r Degree], Sin[ 39 r Degree]}}]}, 
  {r, 0, 360, 1}]

Also looks great in black and white:

enter image description here
POSTED BY: Dariia Porechna

I only knew of these kinds of visualizations:

Graphics[Line[Tuples[N@CirclePoints[17], 2]]]

enter image description here

However yours are much more intricate, very nicely done!

POSTED BY: Sander Huisman
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract