I think this expression should work in Mathematica. If I use the simpler notation in the expression, I can rewrite it as
expr = 1/4 (-1 + 4 c E^(-(1/2) t1 v1) + E^(t2 * v1)) \[Alpha] - ((-1 + E^(t2 *v1)) \[Psi]11)/(2 v1)
This is indeed a simple polynomial in terms of c:
In[93]:= PolynomialQ[expr, c]
Out[93]= True
The coefficients are
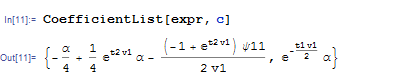
Therefore you can either find the solution via:
Solve[expr==\[alpha],c]
Or use the coefficients in the list above (the first over the second).