Wikipedia article Letter frequency states that according to widely recognized analysis of Concise Oxford dictionary, the sequence of English alphabet letters sorted according to their frequency is:
etaoinshrdlcumwfgypbvkjxqz

Other sources ( 1, 2 ) give similar results. I noticed @Marco Thiel used WordList in this post and obtained a different result. My own effort with the larger dictionary of DictionaryLookup yields also a different result. The question is: How can we reproduce standard letter-frequencies in English language and are these results truly standard ? I will show my analysis below. First of all a few assumptions:
While dictionaries vary in sizes and exact content, we assume due to their large sizes some approximate universal statistics should emerge for all of them. For example, is it just to assume that most frequent letter is "e" for any published large English dictionary?
Count only non-repeating words. Different "InflectedForms" of the same root are fine to count. This is what makes difference between letter frequencies of English Language and of English text corpus. Because "the" being most frequent word adds a higher value to letter "t" frequency, for instance, in the text corpus. But here, and I assume in the mentioned Wikipedia sources, we assume letter frequencies of English Language are in question. And thus we are looking at non-repeating words to guarantee independence LETTER-frequencies from WORD-frequencies.
And another question is: are these assumptions aligned with calculations mentioned in Wikipedia? I will use DictionaryLookup and first get all words in English dictionary:
rawENG = DictionaryLookup[];
rawENG // Length
Out[]= 92518
Let's split complex words, delete duplicates, delete single letters, and lower-case:
splitENG=Select[Union[Flatten[StringCases[ToLowerCase[rawENG],LetterCharacter..]]],StringLength[#]>1&];
splitENG//Length
Out[]= 90813
It still contain non standard English characters:
nonREG = Complement[Union[Flatten[ToLowerCase[Characters[splitENG]]]],Alphabet[]]
Out[]= {"á", "à", "â", "å", "ä", "ç", "é", "è", "ê", "í", "ï", "ñ", "ó", "ô", "ö", "û", "ü"}
Deleting words that contain non standard English characters:
dicENG=DeleteCases[splitENG,x_/;ContainsAny[Characters[x],nonREG]];
dicENG//Length
RandomSample[dicENG,10]
Out[]= 90613
Out[]= {"industrialism", "mathias", "tokenism", "showing", "schmo", "delighting", "seahorse", "longings", "shushing", "interdenominational"}
we still get quite large dictionary with more than 90,000 words. Sorted frequencies of letters in this English dictionary:
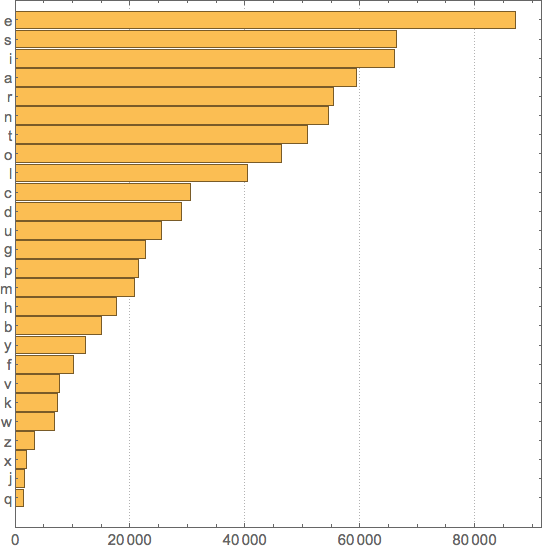
singENGfreq = SortBy[Tally[Flatten[Characters[dicENG]]], Last]
{{"q",1419},{"j",1586},{"x",2069},{"z",3380},{"w",6899},{"k",7411},{"v",7774},{"f",10267},
{"y",12242},{"b",15053},{"h",17717},{"m",20785},{"p",21409},{"g",22682},{"u",25434},
{"d",28939},{"c",30597},{"l",40397},{"o",46441},{"t",50834},{"n",54596},{"r",55354},
{"a",59513},{"i",66084},{"s",66365},{"e",87107}}
We see the sorted sequence is different from Wikipedia. While "e" is by far the most frequent, "t" lost badly its 2nd place. So what is the reason and how we can reproduce standard result?
BarChart[singENGfreq[[All, 2]], BarOrigin -> Left, BaseStyle -> 15,
ChartLabels -> singENGfreq[[All, 1]], AspectRatio -> 1, PlotTheme -> "Detailed"]