Or even, yet simpler:

equation=(x/a)^2+(y/b)^2==1;
equation=equation/.{a->2,b->3}

plot=ContourPlot[Evaluate[equation],{x,-6,6},{y,-6,6},PlotPoints->100,Axes->False,Frame->False];
plot2=PolarPlot[3,{\[Phi],0,2\[Pi]},PlotStyle->None,PlotRange->5,PolarAxes->Automatic,PolarTicks->{"Degrees",Automatic}];
Show[{plot2,plot}]

great answer, as always!

The transformation rules can also be obtained like this:

rules = Thread[{x, y} -> CoordinateTransform[{"Polar" -> "Cartesian", 2}, {r, \[Phi]}]]

which might be easier to grasp...

Another new way of doing the entire thing, including the polar axes is:

equation=(x/a)^2+(y/b)^2==1;
equation=equation/.{a->2,b->3}

rules=Thread[{x,y}->CoordinateTransform[{"Polar"->"Cartesian",2},{r,\[Phi]}]];
equation=equation/.rules;

plot=ContourPlot[Evaluate[equation],{r,0,6},{\[Phi],-\[Pi]+10^-8,\[Pi]},PlotPoints->100];
lines=Cases[Normal[plot],Line[x_]:>Line[FromPolarCoordinates[x]],\[Infinity]];
max=Max[Cases[lines,(x:{_?NumericQ,_?NumericQ}):>Norm[x],\[Infinity]]];
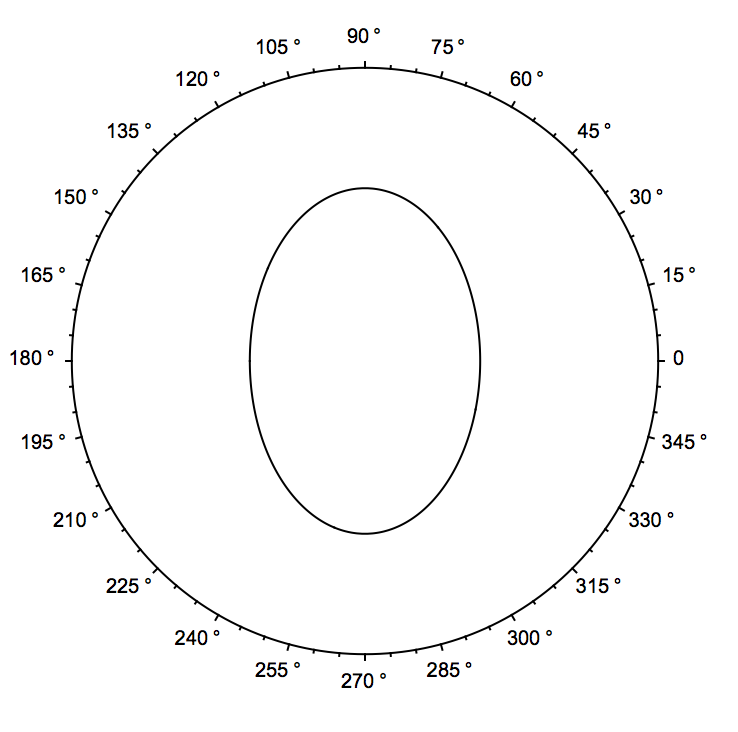
PolarPlot[1.2max,{\[Phi],0,2\[Pi]},Epilog->lines,PlotStyle->None,PlotRange->5,PolarAxes->Automatic,PolarTicks->{"Degrees",Automatic}]

giving: