Coin Permutation Game V2.0. Perfect 3x3 game ( on four arrows ), perfect 5x5 game ( on four arrows ), depictions of solutions and animations.
Game Instantiation
Play Functions
Move[state_, dxy_, n_] := Mod[Plus[state, dxy], n] /. {0 -> n}
SequentialUpdate[GameBoard_, state_, n_] := With[{
next1 =
Move[state[[1]], GameBoard[[ Sequence @@ state[[2]] ]], n ]},
{next1, Move[state[[2]], GameBoard[[ Sequence @@ next1 ]], n ]}
]
SimultaneousUpdate[GameBoard_, state_, n_] := Mod[Plus[state, {
GameBoard[[ Sequence @@ state[[2]] ]],
GameBoard[[ Sequence @@ state[[1]] ]]
}], n] /. {0 -> n}
Board Creation Functions
AllGameBoards[AlphN_, n_] :=
Partition[#, n] & /@ Tuples[Range[0, AlphN - 1], n^2]
Depict[GameBoard_] :=
GraphicsGrid[GameBoard /. {x_Integer, y_Integer} :> Graphics[{
Arrowheads[Medium],
Arrow[{-1/2 Normalize[{y, -x}], 1/2 Normalize[{y, -x}]}]
}, ImageSize -> {50, 50},
PlotRange -> {{-1.1, 1.1}, {-1.1, 1.1}}], Frame -> All]
OneBit = {0 -> {1, 0}, 1 -> {0, 1}};
TwoBit = Join[OneBit, {2 -> {-1, 0}, 3 -> {0, -1}}];
ThreeBit =
Join[TwoBit, {4 -> {1, 1}, 5 -> {-1, 1}, 6 -> {-1, -1},
7 -> {1, -1}}];
AllStates[n_] := Flatten[Outer[{{#1, #2}, {#3, #4}} &,
Range[n], Range[n], Range[n], Range[n]], 3]
Analysis Functions
CycleLengths[Game_, update_] := Length /@ (FindCycle[Graph[
GameGraph[Game /. ThreeBit, update]], Infinity, All])
GameGraph[board_, update_] := With[{n = Length[board]},
MapThread[DirectedEdge, {Range[(n^2)^2],
Position[AllStates[n], update[board, #, n]][[1, 1]] & /@
AllStates[n]}]
]
Games & Analysis
Validation and New Records
EdsGame = {
{0, 2, 3, 3, 2},
{2, 3, 2, 6, 0},
{2, 1, 2, 4, 5},
{3, 1, 1, 2, 3},
{1, 2, 3, 3, 2}};
ErrorGame = {
{1, 3, 2, 2, 3},
{3, 2, 3, 6, 1},
{3, 0, 3, 4, 7},
{2, 0, 0, 3, 2},
{0, 3, 2, 2, 3}};
Cycle625 = {
{2, 0, 0, 1, 0},
{3, 3, 2, 2, 0},
{3, 0, 2, 2, 3},
{0, 3, 3, 2, 0},
{1, 0, 0, 2, 0}} ;
Cycle81 = {
{0, 1, 3},
{3, 2, 0},
{0, 0, 3}};
CycleLengths[EdsGame, SequentialUpdate]
CycleLengths[ErrorGame, SequentialUpdate]
CycleLengths[Cycle625, SequentialUpdate]
CycleLengths[Cycle81, SequentialUpdate]
Out[]={2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 5, 8, 8, 9, 9, 23, 127, 204, 204}
Out[]={2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6, 585}
Out[]={625}
Out[]={81}
GameComparison = Grid[{Show[Depict[# /. ThreeBit], ImageSize -> 300],
Graph[GameGraph[# /. ThreeBit, SequentialUpdate],
EdgeStyle -> Darker[Blue], ImageSize -> 300],
Graph[GameGraph[# /. ThreeBit, SimultaneousUpdate],
EdgeStyle -> Darker[Red], ImageSize -> 300]
} & /@ {EdsGame, ErrorGame, Cycle625,Cycle81},
Frame -> All];
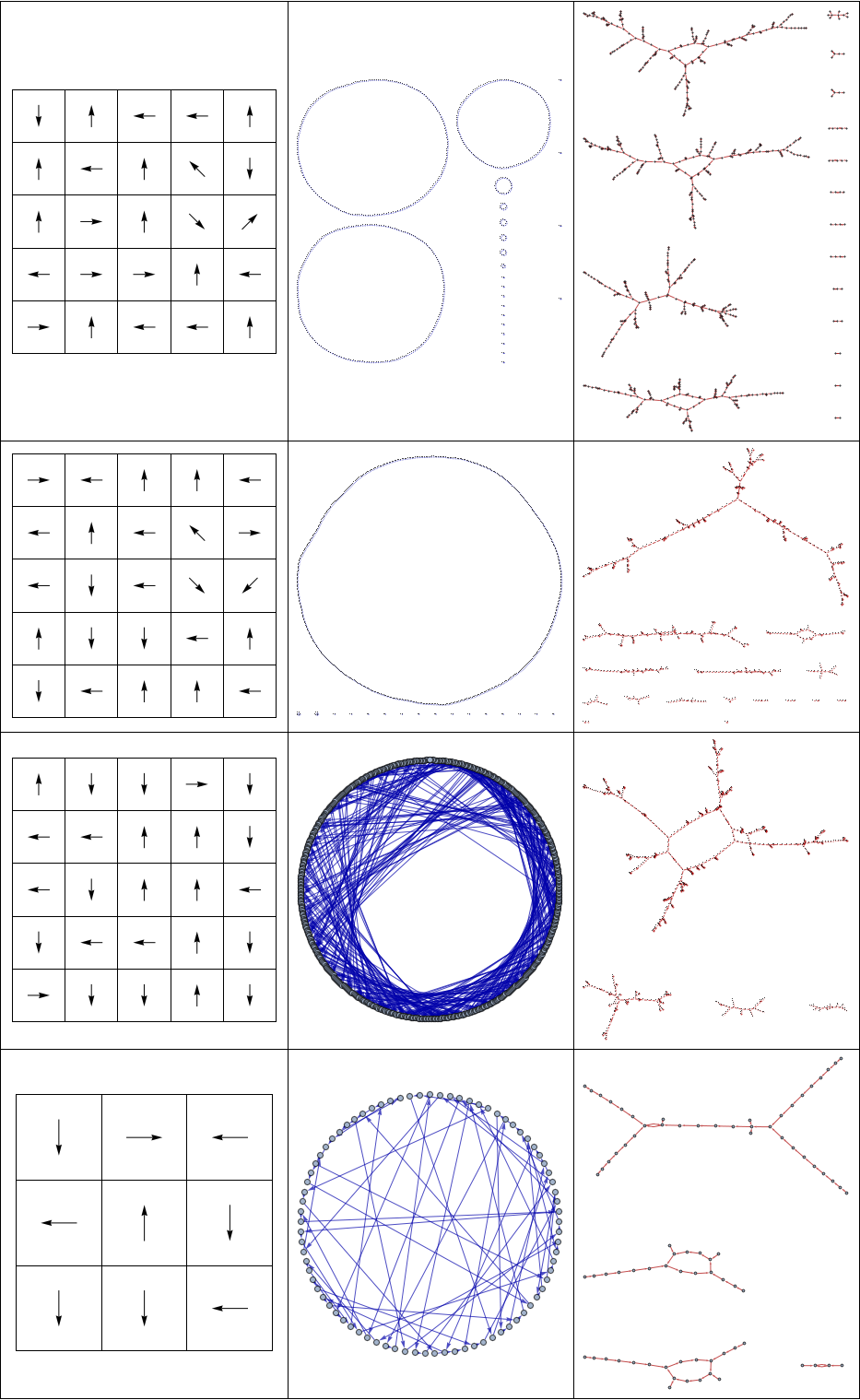
We find perfect games for 3x3 and 5x5 using a gameboard alphabet consisting of only the cardinal directions. Furthermore comparing the affect of sequential vs. simultaneous update accross many game boards, we see that sequential update leads to more cycle topology while simultaneous update leads to branching topology. The figures above show this for a few examples. The "error game" was found by serendipity, and can be obtained from Ed Pegg's earlier game by a map on the directional symbols.
Torus Map
EightyOneGames = {{{0, 1, 3}, {3, 2, 0}, {0, 0, 3}}, {{2, 3, 3}, {0,
3, 0}, {1, 3, 0}}, {{3, 1, 2}, {1, 0, 1}, {0, 0, 1}}}
tori = Row[Function[{a}, Graphics3D[{Thick,
Riffle[{Red, Blue},
Line /@ Transpose[
MapIndexed[#1 /.
{x_Integer, y_Integer} :> {
(1 + x) Cos[2 Pi #2[[1]]/81],
(1 + x) Sin[2 Pi #2[[1]]/81], y} &,
NestList[
SequentialUpdate[EightyOneGames[[a]] /. ThreeBit, #, 3] &,
{{1, 1}, {3, 3}}, 81]]]]}, Boxed -> False,
ImageSize -> 300
]] /@ Range[3]]
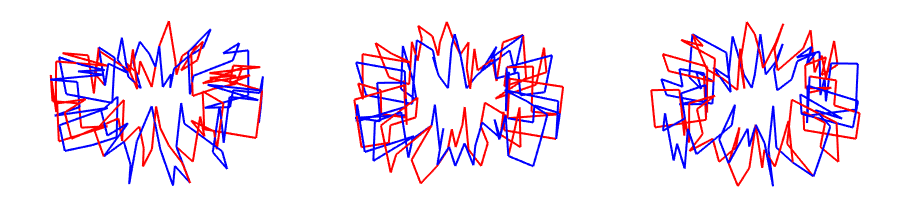
torus625 = Graphics3D[{Thick,
Riffle[{Red, Blue},
Line /@ Transpose[
MapIndexed[#1 /.
{x_Integer, y_Integer} :> {
(5 + x) Cos[2 Pi #2[[1]]/625],
(5 + x) Sin[2 Pi #2[[1]]/625], y} &,
NestList[SequentialUpdate[Cycle625 /. ThreeBit, #, 5] &,
{{1, 1}, {5, 5}}, 625]]]]}, Boxed -> False, ImageSize -> 800
]

Each line tracks the position of a coin through time, and repeats after 81 or 625 equal time intervals. Possibly a joke can be made here regarding KAM theory.
Game Animations
RedDisk = Graphics[{EdgeForm[Thick], Darker@Red, Opacity[.2], Disk[]}];
BlueDisk =
Graphics[{EdgeForm[Thick], Darker@Blue, Opacity[.2], Disk[]}];
RedBlueDisk = Graphics[{Darker@Blue, Disk[{0, 0}, 1, {-Pi/2, Pi/2}],
Darker@Red, Disk[{0, 0}, 1, {3 Pi/2, Pi/2}]}];
GameBoard = Depict[EightyOneGames[[1]] /. ThreeBit];
SequentialUpdate2[GameBoard_, state_, n_] := With[
{next1 =
Move[state[[1]], GameBoard[[ Sequence @@ state[[2]] ]], n ]},
Sow[{next1, state[[2]]}];
{next1, Move[state[[2]], GameBoard[[ Sequence @@ next1 ]], n ]}
]
GetMoves[GameBoard_] :=
With[{moves =
Reap[NestList[
SequentialUpdate2[GameBoard /. ThreeBit, #,
Length@GameBoard] &, {{1,
1}, (Length@GameBoard)*{1, 1}}, (Length@GameBoard)^4]]},
Riffle[moves[[1]], moves[[2, 1]]]
]
GetFrames[GameBoard_] :=
With[{GraphicBoard = Depict[GameBoard /. ThreeBit]},
GetMoves[GameBoard] /. {
{{x_, y_}, {x_, y_}} :>
ReplacePart[
GraphicBoard, {1, 2, x, y, 1} ->
Show[RedDisk, BlueDisk, GraphicBoard[[1, 2, x, y, 1]] ]],
{{x_, y_}, {u_, v_}} :> ReplacePart[GraphicBoard, {
{1, 2, x, y, 1} ->
Show[BlueDisk, GraphicBoard[[1, 2, x, y, 1]] ],
{1, 2, u, v, 1} -> Show[RedDisk, GraphicBoard[[1, 2, u, v, 1]] ]
}]}]
Frames81 = GetFrames[EightyOneGames[[1]] ];
Frames625 = GetFrames[ Cycle625 ];
Manipulate[Frames81[[i]], {i, 1, 2*81 + 1, 1}]
Manipulate[Frames625[[i]], {i, 1, 2*625 + 1, 1}]
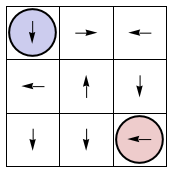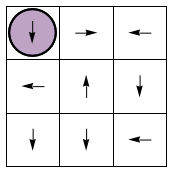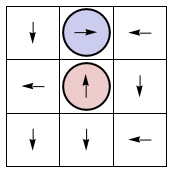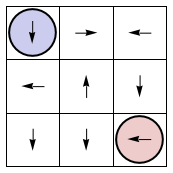
In these animations, the initial condition is in opposing corners, as in a boxing match. Since each trajectory goes through every possible state, eventually some coincident state is reached. Furthermore all 9 or 25 coincident states are reached during time evolution. That's the game!
Conclusions
For a grid of 3x3 or 5x5, 8 directional symbols are not necessary to make a "perfect game", which visits every point in state space. For each of these domains we find perfect games using only four symbols. Is it possible to use only three symbols? Is there a perfect game for every NxN grid? If yes, how to construct?