Consider the following maze.

Here's a directional grid for anyone that would like to try to solve this with a program, followed by a mapping for all the arrows and code to draw the grid.
bg = {{{-1, 0}, {1, 1}, {1, 1}, {1, 1}, {-1, -1}}, {{0, -1}, {0, 1}, {1, -1}, {0, 1}, {1, 0}}, {{0, 1}, {-1, -1}, {-1, 0}, {-1, 1}, {1, 1}}, {{1, -1}, {0, -1}, {0, 1}, {-1, 0}, {0, -1}}, {{0, 1}, {-1, 0}, {1, -1}, {1, 0}, {1, 0}}};
map = Thread[{{-1, -1}, {-1, 0}, {-1, 1}, {0, -1}, {0, 1}, {1, -1}, {1, 0}, {1, 1}} -> {"\[UpperLeftArrow]", "\[UpArrow]", "\[UpperRightArrow]", "\[LeftArrow]", "\[RightArrow]", "\[LowerLeftArrow]", "\[DownArrow]", "\[LowerRightArrow]"}];
Style[Grid[bg /. map, Frame -> All, FrameStyle -> Directive[Thickness[4]]], 70, Bold]
So how might this be solved? It's a 5x5 grid, and there are two coins, so there is a maximum of 25x25=625 positions. These position can be represented by {1,1,1,1} to {5,5,5,5}, with the first two slots for coin 1. The next step is to build all the connections between those positions, and then to make a graph out of it.
positions = Tuples[Range[5], {4}];
grids = {bg, bg};
connects = Join[
Flatten[Table[Select[# \[DirectedEdge] # + Join[{0, 0}, grids[[1, j, k]]] & /@
Select[positions, Take[#, 2] == {j, k} &], Max[#[[2]]] <= 5 && Min[#[[2]]] >= 1 &],{j, 1, 5}, {k, 1, 5}], 3],
Flatten[Table[Select[# \[DirectedEdge] # + Join[grids[[2, j, k]], {0, 0}] & /@
Select[positions, Drop[#, 2] == {j, k} &], Max[#[[2]]] <= 5 && Min[#[[2]]] >= 1 &],{j, 1, 5}, {k, 1, 5}], 3]];
pat = Sort[FindCycle[{Graph[connects], {3, 3, 3, 3}}, {2, 500}, 50000]];
Length /@ Take[pat, 10]
{145, 167, 168, 171, 172, 173, 174, 174, 175, 175}
According to the code run, the shortest solution requires 145 moves. There are thousands of longer solutions. That's incredibly complicated for a 5x5 maze. What does a map of the coins moving for the solution look like?
With[{route = Transpose[MapIndexed[{Append[Take[#1, 2], #2[[1]]/35], Append[Drop[#1, 2], #2[[1]]/35]} &,
Append[First /@ pat[[1]], {3, 3, 3, 3}]]]}, Graphics3D[{Red, Line[route[[1]]], Blue, Line[route[[2]]]}]]
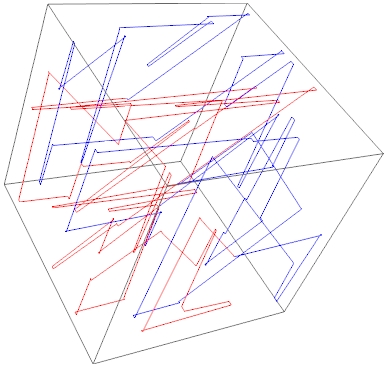
This particular maze was found randomly. Thousands of grids were randomly generated and evaluated for solution complexity, and then some of the superior grids got small random changes to see if anything better came out.
Can anyone else make a more complex maze of this sort?