NOTE: all Wolfram Language code and data are available in the attached notebook at the end of the post.

For my class this fall, I developed a little primer on Association and Dataset that I think might be useful for many people. So, I'm sharing the attached notebook. It's somewhat about the concepts embedded inside these features. It's intended for people at a beginner-intermediate level of Mathematica/Wolfram Language programming, but might be of value even to some more advanced users who have not poked about the Dataset functionality.

The sections of the notebook are:

1. The world before Associations and Datasets
2. Datasets without Associations
3. Enter the Association
4. Creating a Dataset from a List of Associations
5. Nice queries with Dataset
6. Query
7. Some Recipes

The world before Associations and Datasets

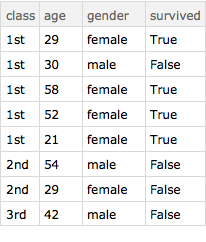
Here' s an array of data. The data happens to represent the cabin class, age, gender, and survival of some of the passengers on the Titanic.

t = {{"1st", 29, "female", True}, {"1st", 30, "male", False}, {"1st", 
    58, "female", True}, {"1st", 52, "female", True}, {"1st", 21, 
    "female", True}, {"2nd", 54, "male", False}, {"2nd", 29, "female",
     False}, {"3rd", 42, "male", False}};

As it stands, our data is a List of Lists.

Head[t]

List

Head /@ t

{List, List, List, List, List, List, List, List}

Suppose I wanted to get the second and fifth rows of the data. This is how I could do it.

t[[{2, 5}]]

{{"1st", 30, "male", False}, {"1st", 21, "female", True}}

Suppose we want to group the passengers by gender and then compute the mean age. We could do this with the following pretty confusing code.

Use and enjoy. Constructive feedback appreciated.

grouped = GatherBy[t, #[[3]] &];
justTheAges = grouped[[All, All, 2]];
Mean /@ justTheAges

{189/5, 42}

Or I could write it as a one liner this way.

Map[Mean, GatherBy[t, #[[3]] &][[All, All, 2]]]

{189/5, 42}

But either way, realize that I have to remember that gender is the third column and that age is the second column. When there is a lot of data, this can get hard to remember.

Datasets without Associations

I could, if I wanted, convert this data into a Dataset. I do this below simply by wrapping Dataset about t. You see there is now some formatting about the data. But there are no column headers (because no one has told Dataset what to use). And there are no row headers, again because no one has told Dataset what to use.

t2 = Dataset[t]

The head of the expression has changed.

Head[t2]

Dataset

Now, I can now access the data in a different way.

Query[{2, 5}][t2]

Or, I can do this. Mathematica basically converts this expression into Query[{2,5}][t2]. The expression t2[{2,5}] is basically syntactic sugar.

t2[{2, 5}]

Digression : Using Query explicitly or using syntactic sugar

Why, by the way would anyone use the longer form if Mathematica does the work for you? Suppose you want to store a Dataset operation -- perhaps a complex series of Dataset operations -- but you want it to work not just on a particular Dataset but on any Dataset (that is compatible). Here's how you could do it.

q = Query[{2, 5}]

Query[{2, 5}]

q[t2]

Now, let' s create a permutation of the t2 Dataset so that the rows are scrambled up.

t2Scrambled = t2[{1, 4, 8, 3, 2, 7, 5}]

We can now run the q operation on t2Scrambled. Notice that the output has changed even though the query has stayed the same.

q[t2Scrambled]

We can also generate Query objects with functions. Here's a trivial example. There are very few languages of which I am aware that have the ability to generate queries by using a function. The one other example is Julia.

makeASimpleQuery[n_] := Query[n]
makeASimpleQuery[{3, 4, 7}][t2]

MapReduce operations on Dataset objects

Now, if I want to know the mean ages of the genders I can use this code. This kind of grouping of data and then performing some sort of aggregation operation on the groups is sometimes known as a MapReduce. (I'm not a fan of the name, but it is widely used). It's also sometimes known as a rollup or an aggregation.

Query[GroupBy[#[[3]] &], Mean, #[[2]] &][t2]

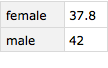
Or this shorthand form in which the Query is constructed.

t2g = t2[GroupBy[#[[3]] &], Mean, #[[2]] &]

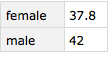
I think this is a little cleaner. But we still have to remember the numbers of the columns, which can be challenging.

By the way, just to emphasize how we can make this all functional, here's a function that creates a query that can run any operation (not just computing the mean) on the Dataset grouped by gender and then working on age.

genderOp[f_] := Query[GroupBy[#[[3]] &], f, #[[2]] &]
genderOp[Max][t2]

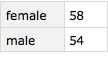
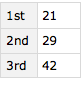
To test your understanding, see if you can find the minimum age for each class of passenger on the Titanic in our Dataset t2.

Query[GroupBy[#[[1]] &], Min, #[[2]] &][t2]

Enter the Association

Review of Association

If you feel comfortable with Associations, you can skip this section; otherwise read it carefully. Basically the key to understanding most Dataset operations is understanding Associations.

Construction of Associations

Now let' s alter the data so that we don't have to remember those facts. To do this we will create an Association. Here's an example called assoc1. Notice that we do so by creating a sequence of rules and then wrapping it in an Association head. Notice that the standard output does not preserve the word "Association" as the head but, just as List is outputted as stuff inside curly braces, Association is outputted as stuff inside these funky "<|" and "|>" glyphs.

assoc1 = Association["class" -> "1st", "age" -> 29, "gender" -> "female", "survived" -> True]

<|"class" -> "1st", "age" -> 29, "gender" -> "female", "survived" -> True|>

I could equivalently have created a list of rules rather than a sequence. Mathematica would basically unwrap the List and create a sequence.

assoc1L = Association[{"class" -> "1st", "age" -> 29, "gender" -> "female", "survived" -> True}]

<|"class" -> "1st", "age" -> 29, "gender" -> "female", "survived" -> True|>

We can use AssociationThread to create Associations in a different way. The first argument is the list of things that go on the left hand side of the Rules -- the "keys" -- and the second argument is the list of things that go on the right hand side of the Rules -- the "values".

assoc1T = AssociationThread[{"class", "age", "gender", "survived"}, {"1st", 29, "female", True}]

<|"class" -> "1st", "age" -> 29, "gender" -> "female", "survived" -> True|>

Now let's use AssociationThread function to create a list of Associations similar to our original data.

convertListToAssociation = 
 list \[Function] 
  AssociationThread[{"class", "age", "gender", "survived"}, list]

Function[list, AssociationThread[{"class", "age", "gender", "survived"}, list]]

I start with t and Map the convertListToAssociation function over the rows of the data. I end up with a list of Associations.

t3 = Map[convertListToAssociation, t]

Keys and Values

Associations have keys and values. These data structures are used in other computer languages but known by different names: Python and Julia call them dictionaries. Go and Scala call them maps. Perl and Ruby call them hashes. Java calls it a HashMap. And Javascript calls it an object. But they all work pretty similarly. Anyway, the keys of an Association are the things on the left hand side of the Rules.

Keys[assoc1]

{"class", "age", "gender", "survived"}

And the values of an Association are the things on the right hand side of the Rules.

Values[assoc1]

{"1st", 29, "female", True}

That' s about all there is too it. Except for one thing. Take a look at the input and output that follows.

assoc2 = Association["a" -> 3, "b" -> 4, "a" -> 5]

<|"a" -> 5, "b" -> 4|>

You can' t have duplicate keys in an Association. So, when Mathematica confronts duplicate keys, it uses the last key it saw. You might think this is a minor point, but it is actually very important in coding. We will see why soon.

Nested Associations

A funny thing happens if you nest an Association inside another Association.

Association[assoc1, assoc2]

<|"class" -> "1st", "age" -> 29, "gender" -> "female", "survived" -> True, "a" -> 5, "b" -> 4|>

You end up with a single un - nested (flat) association. That's a little unusual for Mathematica, but we can exploit this flattening as a way of adding elements to an Association.

Association[Association["dances" -> False], assoc1]

<|"dances" -> False, "class" -> "1st", "age" -> 29, "gender" -> "female", "survived" -> True|>

Or, here' s a function that exploits the flattening to add elements to an Association.

addstuff = Association[#, "dances" -> False, "sings" -> True] &

Association[#1, "dances" -> False, "sings" -> True] &

addstuff[assoc1]

<|"class" -> "1st", "age" -> 29, "gender" -> "female", "survived" -> True, "dances" -> False, "sings" -> True|>

Extracting Values from Associations

Just as the values contained in a List can be accessed by using the Part function, the values contained in an Association can likewise be accessed. Suppose, for example that I wanted to compute double the age of the person in assoc1.

It turns out there are a lot of ways of doing this. The first is to treat the Association as a list except that the indices, instead of being integers, are the "keys" that are on the left hand side of the rules.

2*Part[assoc1, "age"]

58

2*assoc1[["age"]]

58

A second way is to use Query. We can wrap the "key" in the head Key just to make sure Mathematica understands that the thing is a Key.

2*Query[Key["age"]][assoc1]

58

Usually we can omit the Key and everything works fine.

2*Query["age"][assoc1]

58

A third way is to write a function that has an association as its argument.

af = Function[Slot["age"]]

"#age &"

Now look what we can do.

2*Query[af][assoc1]

58

We can shorten this approach by using a simpler syntax for a function.

2*Query[#age &][assoc1]

58

Note, though that this still will not work. Basically, Mathematica is confused. It thinks the function itself is the key.

2*assoc1[af]

2 Missing["KeyAbsent", #age &]

But here' s a simple workaround. For very simple functions, I can just use the name of the key.

2*assoc1["age"]

58

A Note on Slot Arguments

And please pay attention to this : sometimes the Mathematica parser gets confused when it confronts a "slot argument" written as #something. If you see this happening, write it as Slot["something"].

Slot["iamaslot"] === #iamaslot

True

Here' s another problem. What if the key in the association has spaces or non-standard characters in it. Any of these, for example, are perfectly fine keys: the string "I have a lot of spaces in me", the string "Ihaveunderscores", the symbol True, the integer 43. But if we try to denote those keys by putting a hash in front of them, it will lead to confusion and problems.

problemAssociation = Association["I have a lot of spaces in me" -> 1, "I_have_underscores" -> 2, True -> 3, 43 -> 4]

<|"I have a lot of spaces in me" -> 1, "Ihaveunderscores" -> 2, True -> 3, 43 -> 4|>

{Query[#I have a lot of spaces in me &][problemAssociation], 
 Query[#I _have _underescores &][problemAssociation]}

Here' s a solution.

{Query[Slot["I have a lot of spaces in me"] &][problemAssociation], 
 Query[Slot["I_have_underscores"] &][problemAssociation]}

{1, 2}

Here' s how we solve the use of True and an integer as keys. We preface them with Key.

{Query[#True &][problemAssociation], Query[#43 &][problemAssociation]}

{Query[Key[True]][problemAssociation], 
 Query[Key[43]][problemAssociation]}

{3, 4}

Working with Associations and Lists of Associations

Here' s something we can do with the data in the form of an Association. I could ask for the gender of the person in the third row as follows. Notice I did not have to remember that "gender" was generally in the third position.

t3[[3]][["gender"]]

"female"

So, even if I scramble the rows, I can still use the same code.

t3Scrambled = Map[convertListToAssociation, t[[All, {4, 1, 3, 2}]]]

t3Scrambled[[3]][["gender"]]

female

I could also group the people according to their cabin class. Here I use Query on a list of Associations.

Query[GroupBy[#class &]][t3]

Again, the following code, which does not explicitly use Query, won' t work. Basically, nothing has told Mathematica to translate t3[stuff___] [RightArrow]Query[stuff][t3]. If t3 had a head of Dataset, Mathematica would know to make the translation.

t3[GroupBy[#class &]]

I can also get certain values for all the Associations in a list of Associations.

Query[All, #age &][t3]

{29, 30, 58, 52, 21, 54, 29, 42}

I can also map a function onto the result. I don't have to go outside the Query form to do so.

Query[f, #age &][t3]

f[{29, 30, 58, 52, 21, 54, 29, 42}]

Or, without exiting the Query form, I can map a function onto each element of the result.

Query[Map[f], #age &][t3]

{f[29], f[30], f[58], f[52], f[21], f[54], f[29], f[42]}

I could also do the same thing as follows.

Query[All, #age &, f][t3]

{f[29], f[30], f[58], f[52], f[21], f[54], f[29], f[42]}

Creating a Dataset from a List of Associations

To get full use out of Query and to permit syntactic shorthands, we need for Mathematica to understand that the list of Associations is in fact a Dataset. Here' s all it takes.

d3 = Dataset[t3]

We can recover our original list of associations by use of the Normal command.

t3 === Normal[d3]

True

With the data inside a Dataset object we now have pretty formatting. But we have more.

We can still do this. We get the same result but in a more attractive form.

d3g = Query[GroupBy[#class &]][d3]

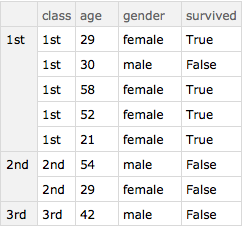
But now this shorthand works too.

d3g = d3[GroupBy[#class &]]

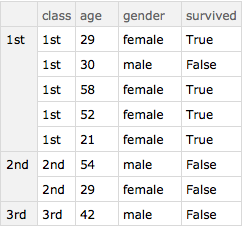
And compare these two elements of code. When the data is in the form of a dataset, Mathematica understands that the stuff in the brackets is not intended as a key but rather is intended to be transformed into a Query.

{Query[#age &][t3[[1]]], d3[[1]][#age &]}

{29, 29}

A Dataset that is an Association of Associations

Let' s look under the hood of d3g.

d3gn = Normal[d3g]

Note : if you really want to look under the hood of a Dataset ask to see the Dataset in FullForm. You can also get more information by running the undocumented package Dataset`, but this is definitely NOT recommended for the non-advanced user.

What we see is an Association in which each of the values is itself a list of Associations.

We can map a function over d3gn.

Map[f, d3gn]

I can of course do the mapping within the Query construct.

Query[All, f][d3gn]

If I try synactic sugar, it doesn' t work because d3gn is not a Dataset.

d3gn[All, f]

Missing["KeyAbsent", All]

But, if I use the Dataset version, it does work. (The first line may be an ellipsis depending on your operating system and display, but if you look under the hood it looks just like the values for 2nd and 3rd. I have no idea why an ellipsis is being inserted.

d3g[All, f]

A Dataset that just has a single Association inside.

We can also have a Dataset that just has a single Association inside. Mathematica presents the information with the keys and values displayed vertically.

Dataset[d3[[1]]]

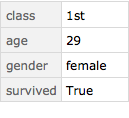
In theory, we could have a Dataset that just had a single number inside it.

Dataset[6]

Nice queries with Dataset

Now I can construct a query that takes a dataset and groups it by the gender column. It then takes each grouping and applies the Mean function to at least part of it. What part? The "age" column part. Notice that I no longer have to remember that gender is the third column and age is the second column.

qd = Query[GroupBy[#gender &], Mean, #age &]

Query[GroupBy[#gender &], Mean, #age &]

Now I can run this query on t3.

qd[d3]

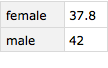
We can now learn a lot about Query. So long as our data is in the form of a Dataset we can write the query as either a formal Query or use syntactic sugar.

Query

A major part of working with data is to understand Query. Let's start with a completely abstract Query, that we will call q1.

q1 = Query[f];

Now let' s run q1 on t3.

q1[t3]

We end up with a list of Associations that has f wrapped around it at the highest level. It's the same as if I wrote the following code.

f[t3] === q1[t3]

True

Now, let' s write a Query that applies the function g at the top level of the list of associations and the function f at the second level, i.e. to each of the rows. Why does it work at the second level? Because it's the second argument to Query.

q2 = Query[g, f];
q2[t3]

The result is the same as if I mapped f onto t3 at its first level and then wrapped g around it.

g[Map[f, t3, {1}]] === q2[d3]
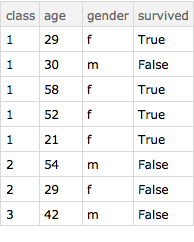
Query[All, MapAt[StringTake[#, 1] &, #, {{"class"}, {"gender"}}] &][d3]

Here' s a function firstchar that takes the first character in a string. firstchar = StringTake[#, 1] &

StringTake[#1, 1] &

Now, let' s construct a query cg1 that applies firstchar to the class and gender keys in each row.

cg1 = Query[All, 
  a \[Function] MapAt[firstchar, a, {{"class"}, {"gender"}}]]

Query[All, Function[a, MapAt[firstchar, a, {{"class"}, {"gender"}}]]]

We apply cg1 to our little dataset d3.

cg1[d3]

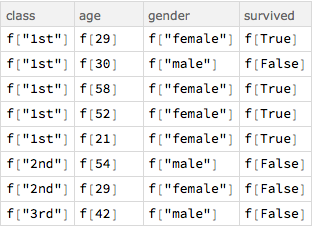
What if we want to apply the same function to every element of the Dataset. We just apply it at the lowest level. Here's one way.

Query[Map[f, #, {-1}] &][d3]

We can also combine it with column wise and entirety wise operations. For reasons that are not clear, Mathematica can't understand this as a Dataset and returns the Normal form.

Query[(Map[f, #, {-1}] &) /* entiretywise, columnwise][d3]

Here' s how we could actually a multilevel Query.

Suppose we want to write a function that computes the fraction of the people in this little dataset that survived. The first step is simply going to be to extract the survival value and convert it to 1 if True and 0 otherwise. There's a built in function Boole that does this.

{Boole[True], Boole[False]}

{1, 0}

q3 = Query[something, 
  assoc \[Function] assoc["survived"] /. {True -> 1, _ -> 0}]

Query[something, Function[assoc, assoc["survived"] /. {True -> 1, _ -> 0}]]

q3[t3]

something[{1, 0, 1, 1, 1, 0, 0, 0}]

So, now we have something wrapping a list of 1 s and 0 s. By making something the Mean function, we can achieve our result.

q4 = Query[Mean, Boole[#survived] &]

Query[Mean, Boole[#survived] &]

q4[d3]

1/2

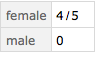
We can also examine survival by gender. Notice that Query is a little like Association: it gets automatically flattened.

Query[GroupBy[#gender &], q4][t3]

<|"female" -> 4/5, "male" -> 0|>

If the data is held in a Dataset, we can also write the final step as follows.

d3[GroupBy[#gender &], q4]

Notice that even if we omit the "Query", this code works. Mathematica just figures out that you meant Query.

The code immediately above is in the form we typically see and often use.

Some Recipes

titanic = ExampleData[{"Dataset", "Titanic"}]

How to add a value to the Dataset based on values external to the existing columns.

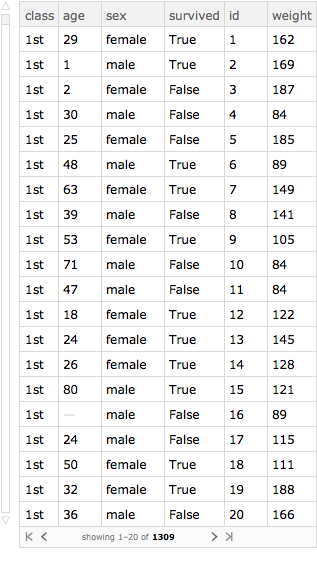
Here' s some additional data. Notice that the data is the same length as the titanic dataset.

stuffToBeAdded = 
 Table[Association["id" -> i, 
   "weight" -> RandomInteger[{80, 200}]], {i, Length[titanic]}]

We use Join at level 2.

augmentedTitanic = Join[titanic, stuffToBeAdded, 2]

How to add a column to a Dataset based on values in the existing columns and to do so row-wise

Notice that the query below does NOT change the value of the titanic dataset. To change the value of the titanic dataset, one would need to set titanic to the result of the computation. Remember, Mathematica generally does not have side effects or do modifications in place.

Query[All, Association[#, "classsex" -> {#class, #sex}] &][titanic]

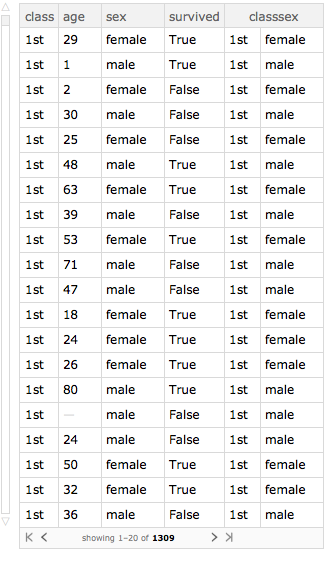
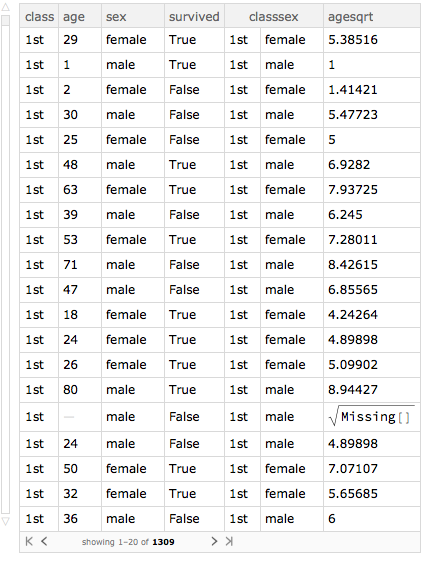
We can add multiple columns this way.

Query[All, 
  Association[#, "classsex" -> {#class, #sex}, 
    "agesqrt" -> Sqrt[#age]] &][titanic]

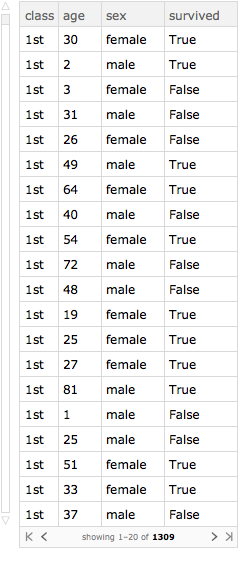
How to change the value of an existing column : row - wise

Age everyone one year.

Query[All, Association[#, "age" -> #age + 1] &][titanic]  

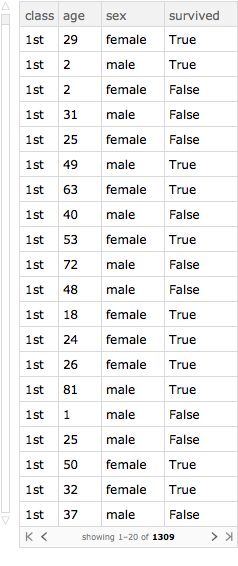
How to change the value of columns selectively.

Query[All, 
  Association[#, 
    "age" -> If[#sex === "male", #age + 1, #age]] &][titanic]

How to create a new column based on some aggregate operator applied to another column.

With[{meanAge = Query[Mean, #age &][titanic]}, 
  Query[All, 
   Association[#, "ageDeviation" -> #age - meanAge] &]][titanic]

Can you develop your own recipes?

Attachments:

The Dataset concept.nb