MODERATOR NOTE: a submission to computations art contest, see more: https://wolfr.am/CompArt-22.
The complete notebook of this post is attached at the end.

This cute little animation came to me while I was playing with Dynamic. I found it very lovely so would like to share it to the community.
So I wanted to know how many Dynamic primitives my 5 years old laptop can handle in one scene (i.e. Graphics). This is my first test scenario:
With[{num = 40, aspRatio = 3, splineOrder = 10},
With[{freqSet = Rescale @ Range @ num},
DynamicModule[
{
y = 0,
pts = Thread[
{
Rescale[Range @ num, {1, num}, aspRatio * {-1, 1}],
0
}
]
},
DynamicWrapper[
Graphics[
{
{
CapForm @ "Round",
Hue[0.58, 0.45, 0.55],
AbsoluteThickness @ 5,
BSplineCurve[
Dynamic @ pts, SplineDegree -> splineOrder, SplineKnots -> "Unclamped"
]
},
{
CapForm @ "Round", JoinForm @ "Round", GrayLevel @ 0.7, AbsoluteThickness @ 3,
Line @ Dynamic @ pts
},
{
Hue[0.1, 0.5, 0.95, 0.7],
AbsolutePointSize @ 20,
Point @ Dynamic @ pts
}
},
PlotRange -> {aspRatio * {-1, 1}, {-1.2, 1.2}},
PlotRangePadding -> Scaled[0.05],
ImageSize -> 600
],
y = Clock[{0, Infinity, 1 / 60}];
pts = MapIndexed[
Function[
{freq, idx},
{
Rescale[idx[[1]], {1, num}, aspRatio * {-1, 1}],
Sin[2 * Pi * freq * y]
}
],
freqSet
]
]
]
]
]

Not too shabby! The motions are smooth, the points align perfectly.
Now this one I call Everlasting Tide:
With[
{
winding = 8, corners = 6, radius = 1, shift = 2, gravityPower = 10, freqPower = 1 / 3, symmetricDir = Pi / 2
},
With[{num = (corners * winding) + 1},
With[
{
ω = Function[Rescale[#, {0, 1}, {0.2, 1}]][
Function[
x,
Plus[
1, -(TriangleWave[{0, 2}, (x - 1) * x] ^ (1 / freqPower))
]
][Rescale @ Range @ num]
]
},
DynamicModule[
{
t = 0,
pts = Function[
Function[
{θ, d},
(radius + d) * {Cos[θ], Sin @ θ}
]@@@#
][
Thread[
{
Rescale[
Range @ num,
{1, num},
{0, winding * 2 * Pi} + symmetricDir
],
0
}
]
]
},
DynamicWrapper[
Graphics[
{
{
Hue[0.1, 0.2, 0.9],
AbsoluteThickness @ 1,
Map[
Circle[{0, 0}, #]&,
Rescale[
Rescale[Range[100]] ^ gravityPower,
{0, 1},
{Max[0, radius + -shift], radius + shift}
]
]
},
{GrayLevel @ 0.85, Line @ Dynamic @ pts},
{
Hue[0, 0.55, 0.85, 0.3],
AbsolutePointSize @ 10,
Point @ Dynamic @ Most @ pts
},
{
GrayLevel[0.7, 0.4],
EdgeForm @ {Black, AbsoluteThickness @ 1},
FilledCurve[BSplineCurve[Dynamic @ Most @ pts, SplineClosed -> True]]
}
},
PlotRange -> ((radius + shift) * {{-1, 1}, {-1, 1}}),
PlotRangePadding -> Scaled[0.05],
Axes -> False, ImageSize -> 500
],
t = Clock[{0, Infinity, 1 / 60}];
pts = Function[
Function[
{θ, d},
(radius + d) * {Cos[θ], Sin @ θ}
]@@@#
][
MapIndexed[
Function[
{ω, idx},
{
Rescale[
idx[[1]],
{1, num},
{0, winding * 2 * Pi} + symmetricDir
],
Times[
shift,
Subtract[
2 * ((Sin[ω * t] + 1) / 2) ^ gravityPower,
1
]
]
}
],
ω
]
]
]
]
]
]
]
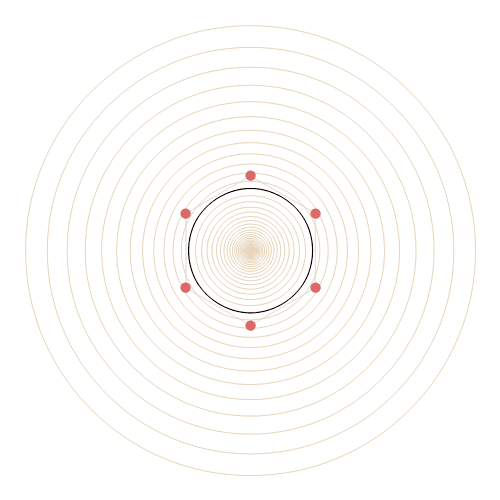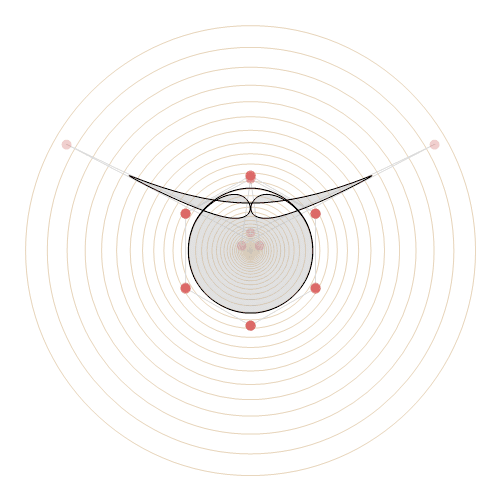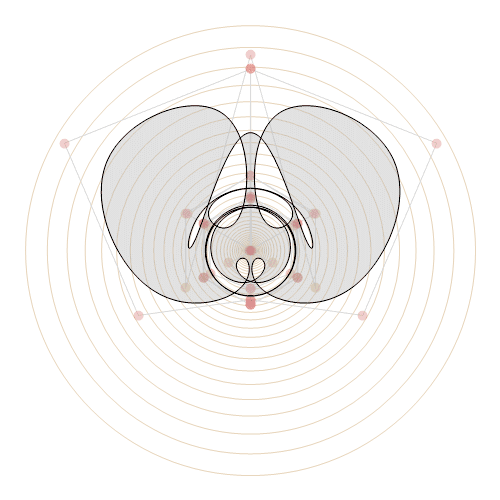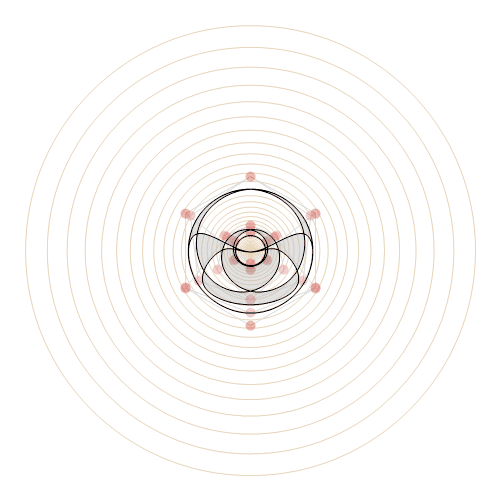
But back to my most beloved animation at the beginning. I introduce to you: Starry Night over Water. A winter night is painted by the palette of the cosmos. Each star whirls in its own delight, unknowingly lighting the quiet water below in a blurry expansion of everchanging hues. I'm really thrilled how such a lovely piece of animation can be created with a little more than 2000 character in code, and the background optimization done by Mathematica to make it run so smoothly.
P.S. I have used explicit iteration here instead of Clock to drive the animation, so that this small quiet world shall be immune from a certain overflow ;)
Things to try:
Playing with the parameters of the outmost With, say, changing baseColorFunc to ColorData["SunsetColors"], or changing aspRatio to match your monitor then menu-bar > Window > FullScreen.
With[
{
(* time step of the animation: *) Δt = 0.05,
(* number of stars: *) n = 50,
(* maximal size of stars: *) radius = 1.5,
(* color theme: *) baseColorFunc = ColorData @ "StarryNightColors",
(* geometric properties of the water region: *)
waterBase = -2, waterWidth = 5,
(* geometric properties of the final drawing: *)
height = 20, imageHeight = 700, aspRatio = 1 / GoldenRatio
},
With[{width = (height + (-waterBase) + waterWidth) / aspRatio},
Apply[
Function[{θ0, ω, expr},
DynamicModule[{θ = θ0},
DynamicWrapper[
Deploy @ Activate @ expr,
θ = Mod[θ + ω * Δt, 2 * Pi]
]
]
]
][
Module[{cx, cy, Δx, Δy, color},
{
RandomReal[{0, Pi / 2}, n],
RandomReal[{0.3, 1}, n],
Inactive[Graphics][
{
(* background: *)
Module[
{
h = height + (-waterBase) + waterWidth + 10,
w = width + 5,
m = 10, Δh, cf = baseColorFunc /* (Darker[#, 0.5]&)
},
Δh = h / m;
MapThread[
Function[
{y, c1, c2},
{
EdgeForm[],
Polygon[
{
{-5, y},
{w, y},
{w, y + Δh},
{-5, y + Δh}
},
VertexColors -> Map[cf, {c1, c1, c2, c2}]
]
}
],
{
Function[
Rescale[
#,
{1, m},
{(waterBase + -waterWidth) - 5, height + 5 + -Δh}
]
][Range @ m],
Most[
Function[0.4 * (1 + -#) ^ 5][Rescale[Range[m + 1]]]
],
Rest[
Function[0.4 * (1 + -#) ^ 5][Rescale[Range[m + 1]]]
]
}
]
],
(* foreground: *)
MapThread[
Function[
{cpos, r, idx, shineShift},
{cx, cy} = cpos;
{Δx, Δy} = cpos + -({width, height} / 2);
(* base color: *)
color = baseColorFunc[
1 + -Norm[{Δx, Δy} / {width, height}, 1]
];
{
(* one star: *)
{
FaceForm @ {Append[(* transparency: *) 0.7][color]},
EdgeForm[],
Polygon[
Map[
Function[cpos + r * #],
{
{0, 1},
{Cos[Dynamic[θ[[idx]]]], 0},
{0, -1},
{-Cos[Dynamic[θ[[idx]]]], 0}
}
]
]
},
(* and its reflection: *)
{
RightComposition[
ColorConvert[#, "LAB"]&,
(* adjust luminance according to shineShift (i.e. y-coords): *)
ReplacePart[
1 -> RightComposition[
Function[Cos[2 * #]],
Function[((# + 1) / 2) ^ 0.5],
Function[
Rescale[
#,
{0, 1},
Plus[
(* mean luminance, lower the brighter: *)
Rescale[shineShift, {-1, 1}, {0.4, 0.7}],
(* luminance variation range, lower the more active: *)
{-1, 1} * Rescale[shineShift, {-1, 1}, {0.3, 0.03}]
]
]
]
][Dynamic[θ[[idx]]]]
],
(* transparency: *)
Append[Function[Rescale[#, {-1, 1}, {0.2, 0.6}]][shineShift]]
][color],
(* abstract blur: *)
AbsoluteThickness[Function[Rescale[#, {-1, 1}, {10, 1}]][shineShift]],
Line[
Function[
{
{
Plus[
cx, -(Times[
r,
Times[
#3,
Times[
1 / 2,
1 + -(#2 * Cos[Dynamic[θ[[idx]]]])
]
]
])
],
#
},
{
Plus[
cx,
Times[
r,
Times[
#3,
(1 / 2) * (1 + #2 * Sin[Dynamic[θ[[idx]]]])
]
]
],
#
}
}
][
(* y-coords: *)
Plus[
waterBase,
waterWidth * ((Rescale[shineShift, {-1, 1}] ^ 0.5) - 1)
],
(* variance: *)
Rescale[shineShift, {-1, 1}, {1, 0.2}],
(* mean radius: *)
Rescale[shineShift, {-1, 1}, {2, 4}]
]
]
}
}
],
{
Join[
ScalingTransform[{3 / 4, 3 / 4}, {width, height} / 2][
RandomPoint[Rectangle[{0, 0}, {width, height}], Ceiling[n / 4]]
],
RandomPoint[
Rectangle[{0, 0}, {width, height}],
(n + -Ceiling[n / 4]) - 1
],
{{width, height} / 2}
],
radius * RandomReal[{1 / height, 1}, n],
Range @ n,
RandomReal[{-1, 1}, n]
}
]
},
PlotRange -> {{0, width}, {waterBase + -waterWidth, height}},
PlotRangePadding -> {{2, 2}, {1, 2}},
Background -> None,
ImageSize -> {Automatic, imageHeight}
]
}
]
]
]
]

 Attachments:
Attachments: