Please download the notebook at the end of the discussion including dynamic feature

July 4th is a fabulous holiday season for American families to enjoy the summer with road trip and BBQ party. You can use a deck of poker to entertain your kids and family friends with James Grime's new card trick on Numberphile.
Background
You are given $10$ cards, from Ace to 10. Shuffle them and split them into $2$ rows with five cards in each. Sort one row in ascending order, the other in descending order. Both orders are oriented from left to right. Calculate the absolute values of the difference between two rows and add them up. You can play the poker game multiple times and you will find the sum is always $25$. If you do not have poker at hand, please take a look at the animation above.
Code
Let's work on the problem with Mathematica to help us understand. In the code I use the icons from this website:
$icon="https://www.iconfinder.com/icons/1331558/card_game_diamond_gambling_game_jewelry_poker_sport_icon";
then I directly assign them to spade and diamond in a notebook:
Use Framed to create a nice and simple poker card:
cardpicture1[{suit_, val_}] := Framed[Column[{val, suit}, Center, 0, ItemSize -> {6, 2},
ItemStyle -> Directive[24, "Label", Bold]], RoundingRadius -> 8]
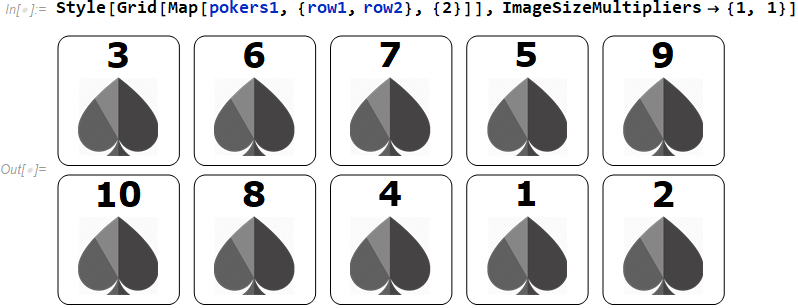
Use Map to create a list of poker cards:
n=10;
numbers = Range[n];
pokers1 = AssociationMap[cardpicture1[{spade, #}] &, numbers];
differences = AssociationMap[cardpicture1[{diamond, #}] &, numbers];
Now lets shuffle the deck of 10 cards:
shuffle=Permute[numbers,RandomPermutation[10]]
(* {3,6,7,5,9,10,8,4,1,2} *)
I use this generic permutation method because you can replace numbers with other list like 10 prime numbers.
Then split it into two rows
{row1,row2}={#[[1;;n/2]],#[[n/2+1;;]]}&[shuffle]
(* {{3,6,7,5,9},{10,8,4,1,2}} *)
Style[Grid[Map[pokers1, {row1, row2}, {2}]], ImageSizeMultipliers -> {1, 1}]
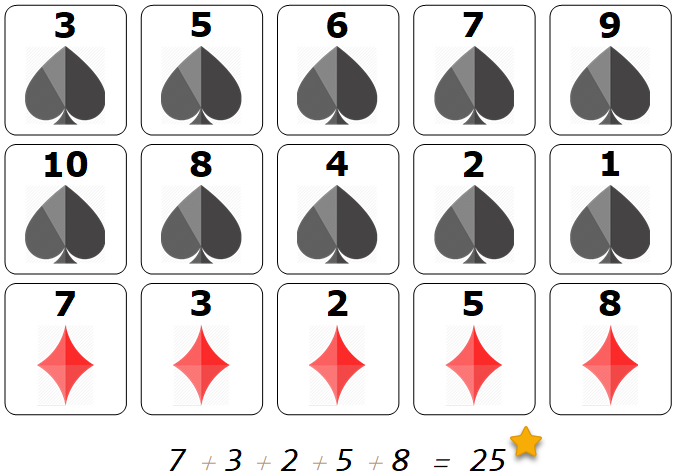
The last two steps are to sort two rows and find the sum of the absolute values of the pairwise differences between the two rows. I use Grid an Style to make the output neat.
With[{r1=Sort@row1,r2=Sort[row2,Greater]},
Module[{sum},sum=Inactive[Plus]@@Abs[r2-r1];
Style[Grid[{
pokers1/@r1,
pokers1/@r2,
(differences/@Abs[r2-r1]),
{Null,SpanFromLeft},
{Style[Row@{sum," = ",Activate[sum]},Large,Italic],SpanFromLeft}}],
ImageSizeMultipliers->{1, 1}]
]
]
Proof
You might already notice I have variables like pokers1 and cardpicture1 in the code above. I am definitely hiding from something from you.
The companion pokers I have, namely pokers2, is a deck of super power cards of which the styles get updated given the face value greater than $5$:
pokers2 = AssociationMap[cardpicture2[{spade, #}] &, numbers];
where
cardpicture2[{suit_, val_}] :=
Framed[Column[{val, suit}, Center, 0, ItemSize -> {6, 2},
ItemStyle -> Directive[24, "Label", Bold]],
FrameStyle -> Directive[If[val > 5, Dashed, Black]],
RoundingRadius -> 8]
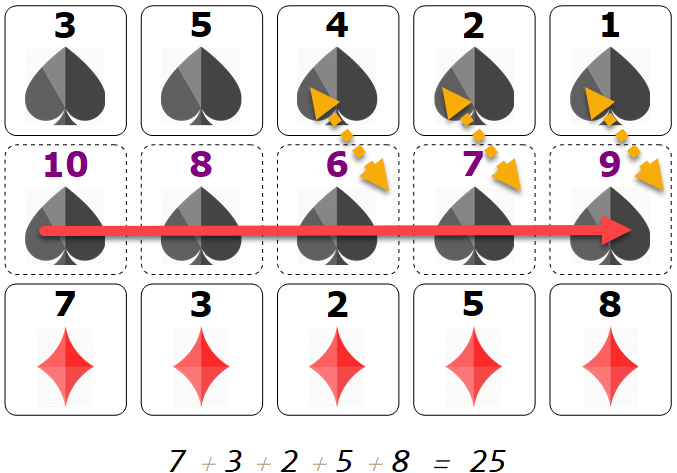
Once we use the super power card, we can see a pattern matches exactly what James claimed in the Numberphile video (using contradiction of stacking dashed/purple numbered card):
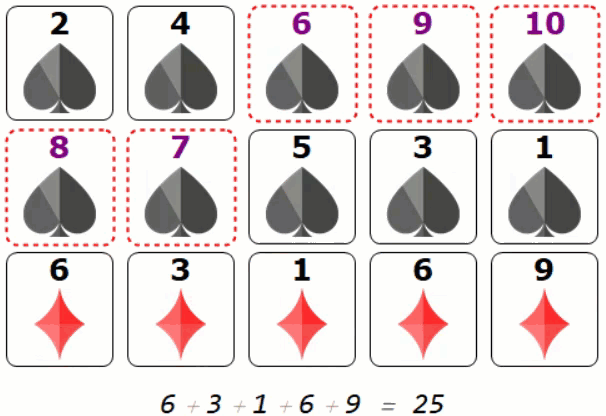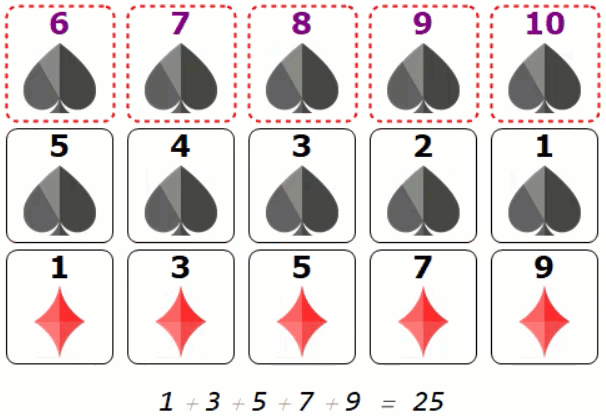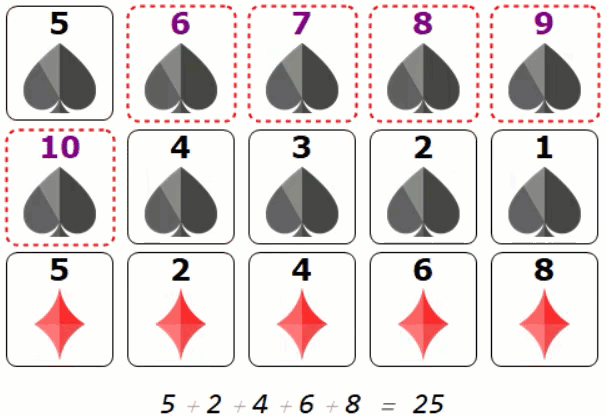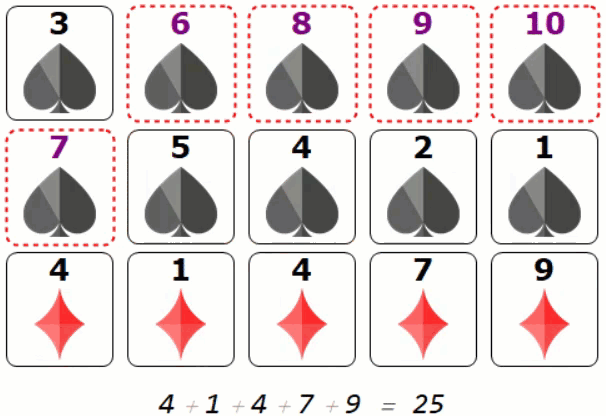
Lets take look at one frame:
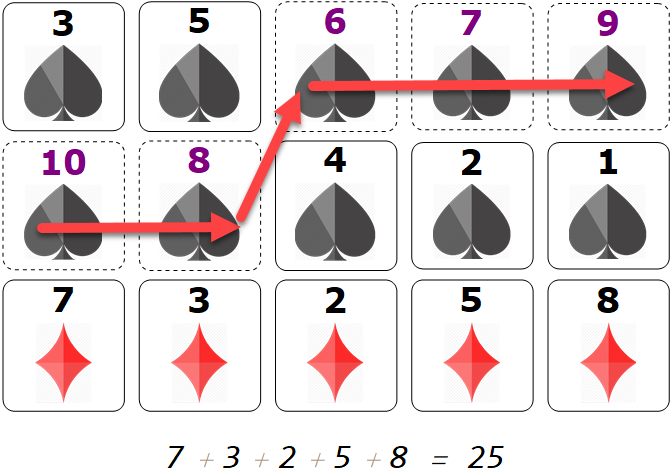
The third diamond line is from the following flipping transition (dash-solid or purple-black)
$ 25 = 7 + 3 + 2 + 5 + 8$
$ = (10 - 3) + (8 - 5 ) + (6 - 4 )+ (7 - 2 ) + (9 - 1) $
$= (10 + 9 + 8 + 7 + 6) -(1 + 2 + 3 + 4 + 5)$
The sorted rows tells you that all dashed card must sit together. Same happens to the solid line cards. Therefore there is exactly one transition from solid -> dash or dash -> solid in each row.
If dashed cards overlapping vertically means we either have at least 6 such cards or one row is not properly sorted. This is contradiction.
Comment
There are nice functions used here
- Use
Inactive[Plus]@@{...} and then to active the sum expression with Activate[]: prints nice hold sum formula and delayed evaluation
AssociationMap to create key-poker face dictionary- Animation is generated by Refresh. Attached at the end of the thread.
- Poker design code is from this demonstration
Code snippet just for the calculation (minimum visualization):
n = 12;
{row1, row2} = {#[[1 ;; n/2]], #[[n/2 + 1 ;;]]} &[Permute[Range[n], RandomPermutation[n]]]
f[m_] := If[m > n/2, Framed[m], m]
{Grid[{row1,row2}],Sequence@@With[{r1=Sort@row1,r2=Reverse@Sort@row2},{Grid[Map[f,{r1,r2},{2}]],Abs[r1-r2]//Total}]}

Formula:
Sum[k, {k, 2*m}] - 2*Sum[k, {k, m}] // Simplify
(* m^2 *)
 Attachments:
Attachments: