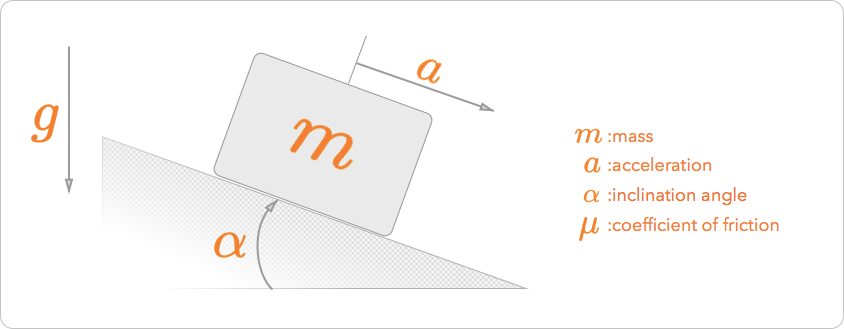
As I understood, you are talking about a Mass on an inclined rough surface.
I have used the numerical solve function to get a somhow simplistic answer. What is more important, however, is to add some simplification to your expression, as follows:
- Set C[1] to zero. (the infinite term of 2 pi C[1] is due to the presence of the trignometric functions.)
- Mu (the coefficient of friction) is Real and greater than zero.
- alpha is Real and has a value between 0 degree (no inclination) and 90 degrees (the surface is vertical).
FullSimplify[
NSolve[a ==
g (Sin[\[Alpha] \[Degree]] - \[Mu] Cos[\[Alpha] \[Degree]]), \
\[Alpha]] /.
C[1] -> 0, {{\[Mu], \[Alpha], a} \[Element] Reals, \[Mu] > 0,
90 >= \[Alpha] >= 0}] // Rationalize
the result is:
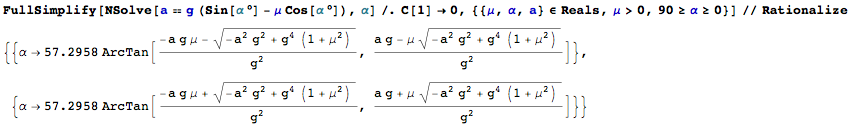
Taking the second answer, which is more physically reasonable:
57.2958 ArcTan[(-a g \[Mu] + Sqrt[-a^2 g^2 + g^4 (1 + \[Mu]^2)])/
g^2, (a g + \[Mu] Sqrt[-a^2 g^2 + g^4 (1 + \[Mu]^2)])/g^2]
Checking the angle for different accelerations:
Table[57.29577951308232` ArcTan[(-a g \[Mu] +
Sqrt[-a^2 g^2 + g^4 (1 + \[Mu]^2)])/g^2, (
a g + \[Mu] Sqrt[-a^2 g^2 + g^4 (1 + \[Mu]^2)])/g^2] /. {\[Mu] ->
0.2, g -> 9.81}, {a, {0, 1, 2, 3, 6, 7, 9.81}}]
the result is:
{11.3099, 17.0466, 22.8419, 28.7598, 48.1615, 55.7129, 90.}
Which I believe is quite good. At zero acceleration, the angle is 11.3099 (the mass is not sliding due the roughness of the surface). And when the acceleration is equal to gravity (the mass is freely falling), the angle is 90 degrees.
I hope this helps @Seokin in any way.
Regards...