I don't think that will work out very well as it stands - there are disconnected pieces (although you might be able to print each one separately). I tried:
shape = RegionPlot3D[x^2 + y^2 - x^2*z + y^2*z + z^2 - 1 < 0.25,
{x, -3, 3},
{y, -3, 3},
{z, -3, 3},
Mesh -> 20,
Boxed -> False,
Axes -> None,
PlotStyle -> Thickness[.1]]
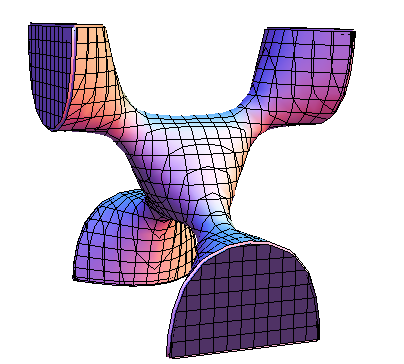
Export["/Users/me/Desktop/shape.stl", shape]
It's close to being printable, at least - but obviously not identical to the plot you want. If you print it in inches, it's 6 inches across. You will want to experiment with increasing the "detail" (PlotPoints -> n, for example). And the shape might require 'fixing' in an external program, because Mathematica doesn't always get the geometry right inside shapes (for example, there might be self-intersecting surfaces, etc.) In my experience it isn't always as easy as people say.
