This is part of a series where I explore some of the videos of Numberphile, see also the other ones:
Today we are gonna look at the graphs from https://www.youtube.com/watch?v=o8c4uYnnNnc
The first can be really easily made:
n = 3^5 - 1;
nums = FromDigits[IntegerDigits[#, 3] /. 2 -> -1, 3] & /@ Range[n];
ListPlot[nums]
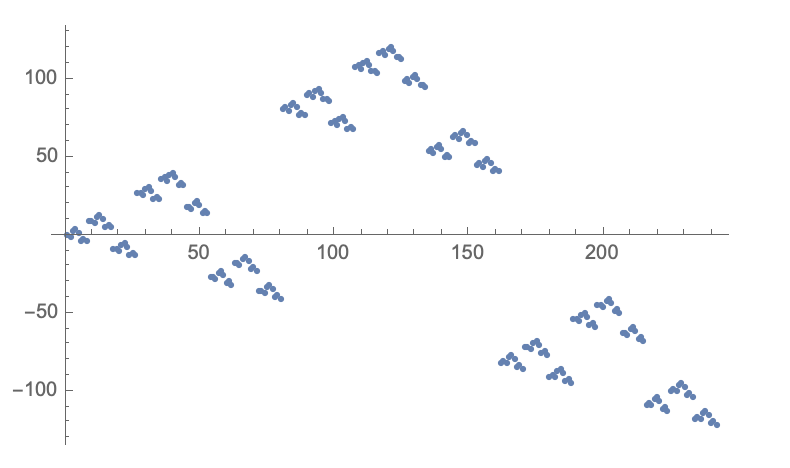
The second can also be easily made using the following code:
n = 1000;
nums = # - (Times @@ DeleteCases[IntegerDigits[#], 0]) & /@ Range[n];
ListPlot[nums]
giving:
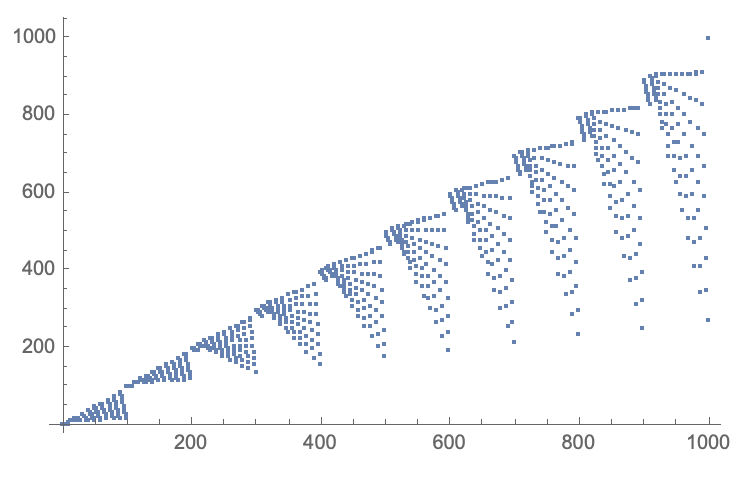
The last sequence is harder to program, especially if one wants a fast solution
Here is the code:
x = ConstantArray[1, 10^5];
x[[;; 2]] = {1, 1};
Dynamic[i]
AbsoluteTiming@Do[
max = Floor[(i - 1)/2];
invalid = 2 x[[i - max ;; i - 1]] - x[[i - 2 max ;; i - 2 ;; 2]];
invalid = Pick[invalid, 1 - UnitStep[-invalid], 1]; (*
remove nonpositive *)
invalid = Sort[DeleteDuplicates[invalid]];
new = -1;
If[Last[invalid] == Length[invalid],
new = Length[invalid] + 1;
,
Do[
If[invalid[[k]] =!= k,
new = k;
Break[];
]
,
{k, 1, Length[invalid]}
];
If[new == -1, new = Last[invalid] + 1];
];
x[[i]] = new;
,
{i, 3, Length[x]}
]
ListPlot[x]
giving:
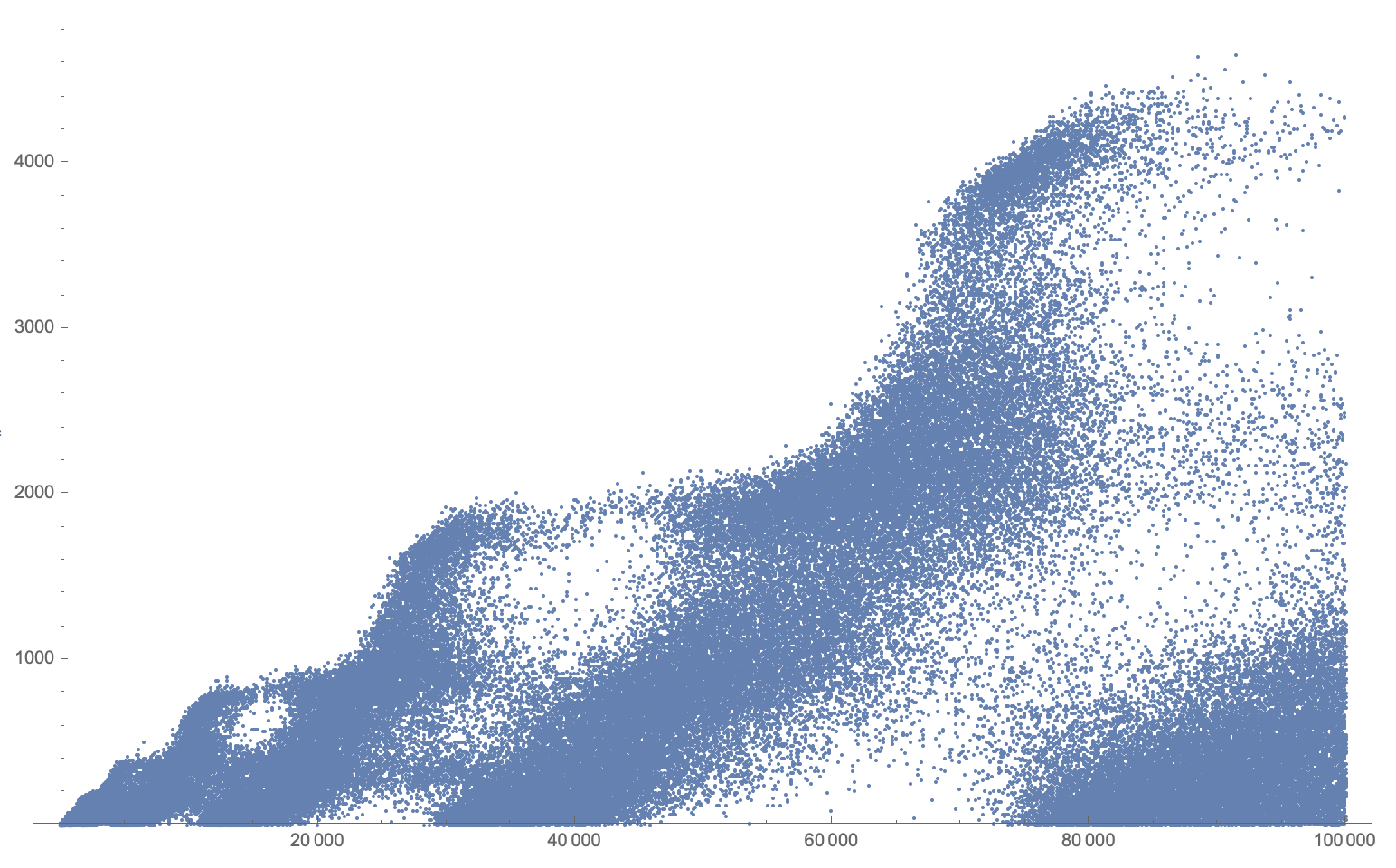
Hope you enjoyed these codes, perhaps you can modify them and make them more intricate/faster/better!