This is part of a series where I explore some of the videos of Numberphile, see also the other ones:
Today we are gonna look at another video on graphs: https://www.youtube.com/watch?v=j0o-pMIR8uk
The first sequence (https://oeis.org/A002487) can, conveniently be recreated by using Riffle:
data = NestList[Riffle[#, Total /@ Partition[#, 2, 1]] &, {1, 1}, 13];
data = Join @@ data[[All, ;; -2]];
ListPlot[data]
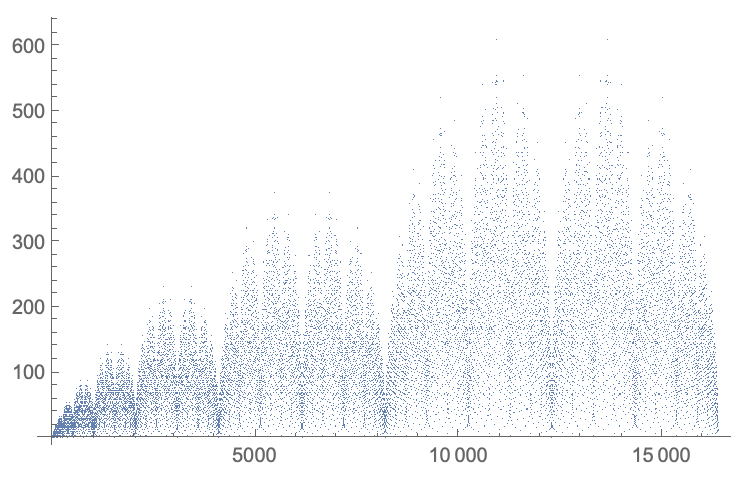
The second sequence (https://oeis.org/A005185) can be recreated like this:
Dynamic[i]
n = 100000;
x = ConstantArray[1, n];
Do[
os = {x[[i - 2]], x[[i - 1]]};
tot = x[[i - os]];
x[[i]] = Total[tot];
,
{i, 3, n}
]
giving:
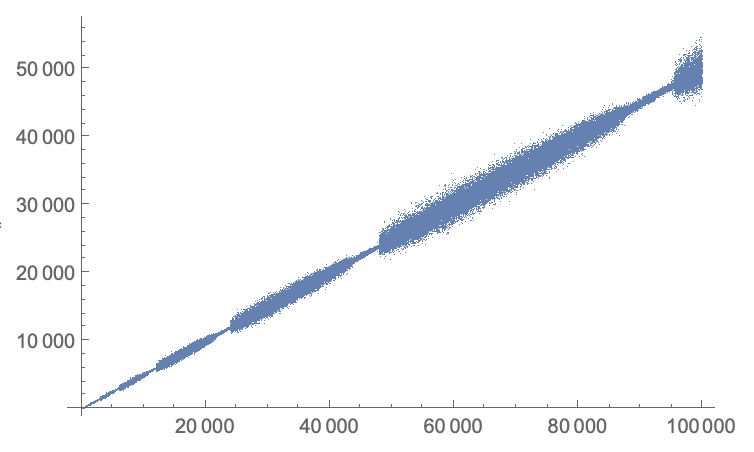
An alternative view would be to plot it logarithmically in the horizontal direction, and to divide the sequence by the index of each number:
tmp = N[x];
tmp /= Range[Length[tmp]];
ListLogLinearPlot[tmp, PlotRange -> All]
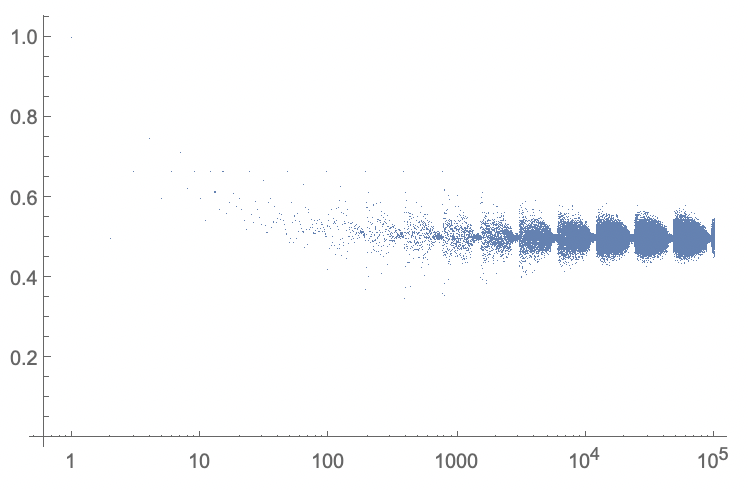
The last sequence (https://oeis.org/A279125) can be recreated like this:
n=1000;
x=ConstantArray[0,n];
Dynamic[i]
Do[
k=-1;
ok=False;
While[!ok,
k++;
good=True;
Do[
If[x[[j]]==k,
If[BitAnd[i,j]>0,
good=False;
Break[];
]
]
,
{j,1,i-1}
];
If[good==True,
x[[i]]=k;
Break[];
]
]
,
{i,2,n}
]
ListPlot[x]
giving:
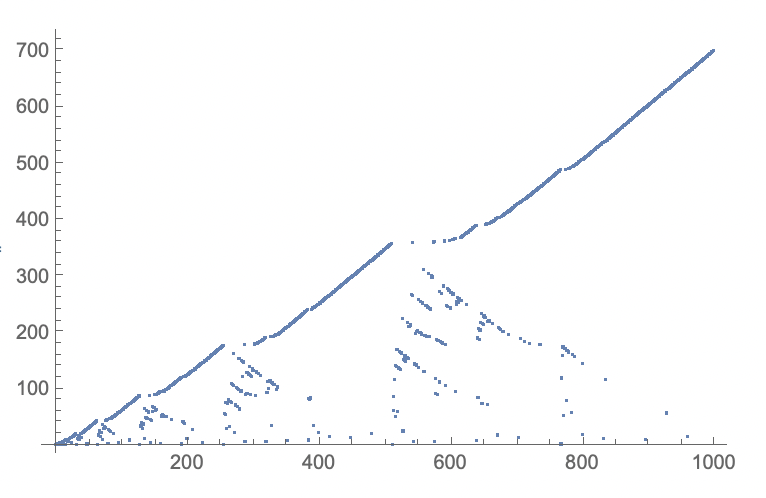
Perhaps someone can provide a faster implementation? Hope you enjoyed these codes, perhaps you can modify them and make them more intricate/faster/better!