Message Boards Message Boards

Converting OpenPose for Wolfram Language

Kotaro Okazaki, FTI
Posted 5 years ago

Tuseeta-san's post is how to convert a trained model of TensorFlow to Mathematica. Converting trained models from a language other than Mathematica to Mathematica is very beneficial to Mathematica users. So I'll show how to convert a trained model of PyTorch to Mathematica along with Tuseeta-san's post. enter image description here

Step 1: Figure out the architecture

The model to be converted is Pose Estimation that detects the human skeleton (body parts and their connections) from an image. It's called OpenPose.The model consists of Feature map that extracts image features and six Stage maps. Feature map extracts image features from an input image(size:368*368). Each Stage map has two-branch, the first branch predicts confidence and the second predicts PAFs?Part Affinity Fields), along with the image feature .Two-branch are concatenated for next stage.

Step 2: Coding it in Mathematica

Feature map

The Feature map consists of the first 23 layers of VGG-19, followed by 2 sets of Convolution and Ramp.

Extract the first 23 layers of VGG-19.

vgg19 = NetModel["VGG-19 Trained on ImageNet Competition Data"];
vgg19sub = Take[vgg19, {1, 23}];

Change Encoder.

enc = NetExtract[vgg19, "Input"];
enc = NetReplacePart[
   enc, {"ImageSize" -> {368, 368}, 
    "VarianceImage" -> {0.229, 0.224, 0.225}, 
    "MeanImage" -> {0.485, 0.456, 0.406}}];
featurefirst = NetReplacePart[vgg19sub, "Input" -> enc];

Add Convolution and Ramp.

feature = 
  NetAppend[
   featurefirst, {"convadd1" -> 
     ConvolutionLayer[256, 3, "Stride" -> 1, "PaddingSize" -> 1], 
    "reluadd1" -> Ramp,
    "convadd2" -> 
     ConvolutionLayer[128, 3, "Stride" -> 1, "PaddingSize" -> 1], 
    "reluadd2" -> Ramp}];

Stage map

Each Stage map consists only of Convolutions and Ramps.

Stage 1: The differences between two branches is that the last output channel number is 38 or 19.

blk11 = NetChain[{
    ConvolutionLayer[128, 3, "Stride" -> 1, "PaddingSize" -> 1], Ramp,
    ConvolutionLayer[128, 3, "Stride" -> 1, "PaddingSize" -> 1], Ramp,
    ConvolutionLayer[128, 3, "Stride" -> 1, "PaddingSize" -> 1], Ramp,
    ConvolutionLayer[512, 1, "Stride" -> 1, "PaddingSize" -> 0], Ramp,
    ConvolutionLayer[38, 1, "Stride" -> 1, "PaddingSize" -> 0]}];
blk12 = NetChain[{
    ConvolutionLayer[128, 3, "Stride" -> 1, "PaddingSize" -> 1], Ramp,
    ConvolutionLayer[128, 3, "Stride" -> 1, "PaddingSize" -> 1], Ramp,
    ConvolutionLayer[128, 3, "Stride" -> 1, "PaddingSize" -> 1], Ramp,
    ConvolutionLayer[512, 1, "Stride" -> 1, "PaddingSize" -> 0], Ramp,
    ConvolutionLayer[19, 1, "Stride" -> 1, "PaddingSize" -> 0]}];

Stage 2?6: The difference between Stage1 and Stage2?6 is the kinds and the numbers of layers.

blkx1 = NetChain[{
    ConvolutionLayer[128, 7, "Stride" -> 1, "PaddingSize" -> 3], Ramp,
    ConvolutionLayer[128, 7, "Stride" -> 1, "PaddingSize" -> 3], Ramp,
    ConvolutionLayer[128, 7, "Stride" -> 1, "PaddingSize" -> 3], Ramp,
    ConvolutionLayer[128, 7, "Stride" -> 1, "PaddingSize" -> 3], Ramp,
    ConvolutionLayer[128, 7, "Stride" -> 1, "PaddingSize" -> 3], Ramp,
    ConvolutionLayer[128, 1, "Stride" -> 1, "PaddingSize" -> 0], Ramp,
    ConvolutionLayer[38, 1, "Stride" -> 1, "PaddingSize" -> 0]}];
blkx2 = NetChain[{
    ConvolutionLayer[128, 7, "Stride" -> 1, "PaddingSize" -> 3], Ramp,
    ConvolutionLayer[128, 7, "Stride" -> 1, "PaddingSize" -> 3], Ramp,
    ConvolutionLayer[128, 7, "Stride" -> 1, "PaddingSize" -> 3], Ramp,
    ConvolutionLayer[128, 7, "Stride" -> 1, "PaddingSize" -> 3], Ramp,
    ConvolutionLayer[128, 7, "Stride" -> 1, "PaddingSize" -> 3], Ramp,
    ConvolutionLayer[128, 1, "Stride" -> 1, "PaddingSize" -> 0], Ramp,
    ConvolutionLayer[19, 1, "Stride" -> 1, "PaddingSize" -> 0]}];

Finally, create OpenPose.

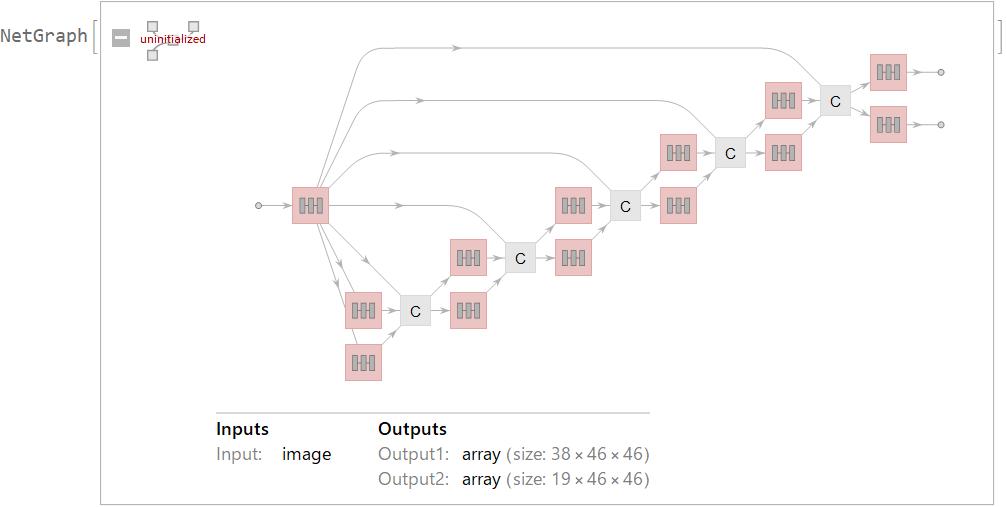
openpose = NetGraph[{
   "feature" -> feature,(*feature*)
   "blk11" -> blk11, "blk12" -> blk12,(*stage 1*)
   "blk21" -> blkx1, "blk22" -> blkx2,(*stage 2*)
   "cat12" -> CatenateLayer[],
   "blk31" -> blkx1, "blk32" -> blkx2,(*stage 3*)
   "cat23" -> CatenateLayer[],
   "blk41" -> blkx1, "blk42" -> blkx2,(*stage 4*)
   "cat34" -> CatenateLayer[],
   "blk51" -> blkx1, "blk52" -> blkx2,(*stage 5*)
   "cat45" -> CatenateLayer[],
   "blk61" -> blkx1, "blk62" -> blkx2,(*stage 6*)
   "cat56" -> CatenateLayer[]
   },
  {"feature" -> "blk11", "feature" -> "blk12",(*stage 1*)
   {"blk11", "blk12", "feature"} -> "cat12",(*stage 2*)
   "cat12" -> "blk21", "cat12" -> "blk22",
   {"blk21", "blk22", "feature"} -> "cat23",(*stage 3*)
   "cat23" -> "blk31", "cat23" -> "blk32",
   {"blk31", "blk32", "feature"} -> "cat34",(*stage 4*)
   "cat34" -> "blk41", "cat34" -> "blk42",
   {"blk41", "blk42", "feature"} -> "cat45",(*stage 5*)
   "cat45" -> "blk51", "cat45" -> "blk52",
   {"blk51", "blk52", "feature"} -> "cat56",(*stage 6*)
   "cat56" -> "blk61", "cat56" -> "blk62"
   }]

enter image description here

Step 3: Importing the Weights and the Biases

Download "posemodelscratch.pth" as a trained model of PyTorch.

Import the parameters, the weights and the biases. I referred "How to import python pickle *.pkl?"

session = StartExternalSession["Python-NumPy"];
parameters = ExternalEvaluate[session, "import torch
import numpy as np
import pickle as pkl

net_weights = torch.load(
       'pose_model_scratch.pth', map_location={'cuda:0': 'cpu'})
keys = list(net_weights.keys())

parameters = {}
for i in range(len(keys)):
       t = net_weights[keys[i]]       
       x = t.numpy()
       parameters[keys[i]] = x.flatten()
parameters"];
DeleteObject[session];

keys = Keys[parameters];
parameters = Values[parameters];

Step 4: Parsing the Weights and the Biases

The parameters is 184 sets of one-dimensional lists. They consists of the Weights and the Biases of 92 Convolution layers in OpenPose.

Get a list of layer names for OpenPose with depth level. Then, get a list of 92 names where convolution layer is used in it.

layernames = 
  GroupBy[Keys@NetInformation[openpose, "Layers"], First] // Values;
convlayernames = (Position[
     NetInformation[openpose, "Layers"], _ConvolutionLayer] // 
    Flatten)[[All, 1]]

enter image description here

As you can see in keys, you can see that the order of convolution layers of OpenPose is different from the order of convolution layers of "posemodelscratch.pth" 

 keys

enter image description here

So, manually sort the order of convolution layers in OpenPose into the order of "posemodelscratch.pth"

convlayernamesGH = {{"feature", "conv1_1"}, {"feature", "conv1_2"},
   {"feature", "conv2_1"}, {"feature", "conv2_2"},
   {"feature", "conv3_1"}, {"feature", "conv3_2"}, {"feature", "conv3_3"}, {"feature", "conv3_4"},
   {"feature", "conv4_1"}, {"feature", "conv4_2"},
   {"feature", "convadd1"}, {"feature", "convadd2"},
   {"blk11", 1}, {"blk11", 3}, {"blk11", 5}, {"blk11", 7}, {"blk11", 9},
   {"blk21", 1}, {"blk21", 3}, {"blk21", 5}, {"blk21", 7}, {"blk21", 9}, {"blk21", 11}, {"blk21", 13},
   {"blk31", 1}, {"blk31", 3}, {"blk31", 5}, {"blk31", 7}, {"blk31", 9}, {"blk31", 11}, {"blk31", 13},
   {"blk41", 1}, {"blk41", 3}, {"blk41", 5}, {"blk41", 7}, {"blk41", 9}, {"blk41", 11}, {"blk41", 13},
   {"blk51", 1}, {"blk51", 3}, {"blk51", 5}, {"blk51", 7}, {"blk51", 9}, {"blk51", 11}, {"blk51", 13},
   {"blk61", 1}, {"blk61", 3}, {"blk61", 5}, {"blk61", 7}, {"blk61", 9}, {"blk61", 11}, {"blk61", 13},
   {"blk12", 1}, {"blk12", 3}, {"blk12", 5}, {"blk12", 7}, {"blk12", 9},
   {"blk22", 1}, {"blk22", 3}, {"blk22", 5}, {"blk22", 7}, {"blk22", 9}, {"blk22", 11}, {"blk22", 13},
   {"blk32", 1}, {"blk32", 3}, {"blk32", 5}, {"blk32", 7}, {"blk32", 9}, {"blk32", 11}, {"blk32", 13},
   {"blk42", 1}, {"blk42", 3}, {"blk42", 5}, {"blk42", 7}, {"blk42", 9}, {"blk42", 11}, {"blk42", 13},
   {"blk52", 1}, {"blk52", 3}, {"blk52", 5}, {"blk52", 7}, {"blk52", 9}, {"blk52", 11}, {"blk52", 13},
   {"blk62", 1}, {"blk62", 3}, {"blk62", 5}, {"blk62", 7}, {"blk62", 9}, {"blk62", 11}, {"blk62", 13}
   };

Get the position of each element of convlayernamesGH in OpenPose.

convlayerpos = 
 Flatten[Position[layernames, #] & /@ convlayernamesGH, 1]

enter image description here

Reshape each one-dimensional list of parameters to the dimension of the corresponding weight or bias.

getDimB[layer_] := Dimensions@NetExtract[layer, "Biases"]
getDimW[layer_] := Dimensions@NetExtract[layer, "Weights"]
convs = NetExtract[NetInitialize[openpose], #] & /@ convlayerpos;
dimW = getDimW /@ convs;
dimB = getDimB /@ convs;
dim = Flatten[Transpose[{dimW, dimB}], 1];
parametersReshape = MapThread[ArrayReshape, {parameters, dim}];

Step 5: Linking the Weights and the Biases

Replace the initial values of weights and biases in OpenPose with learned parameters, and finally get trained OpenPose.

replacenames =
  Flatten[
   Transpose[{Flatten@{#, "Weights"} & /@ convlayernamesGH, 
     Flatten@{#, "Biases"} & /@ convlayernamesGH}], 1];
rule = Thread[replacenames -> parametersReshape];
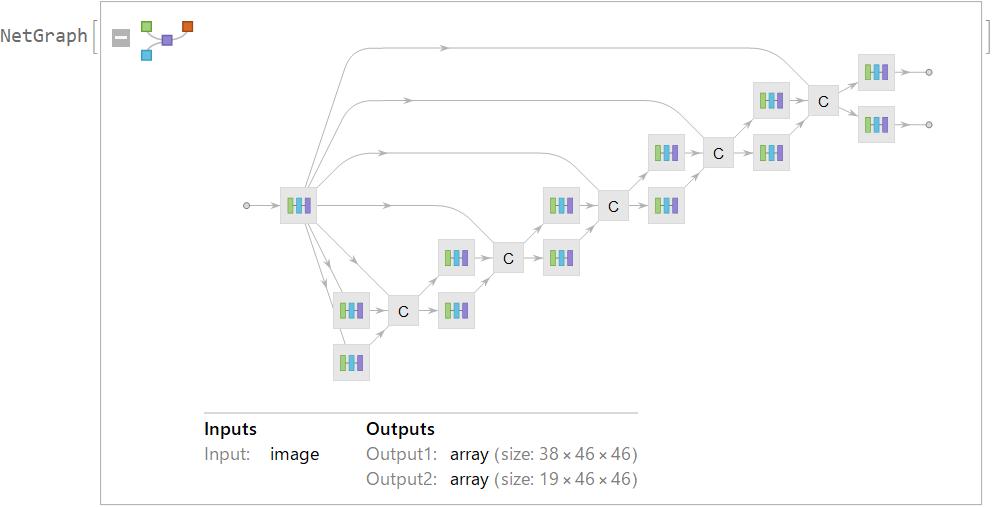
trainedOpenPose = NetReplacePart[openpose, rule]

enter image description here

Step 6: Making the tests

For simplification, estimate pose for the image of single-person. The Output2 of OpenPose shows the confidence of 19 body parts in each part where the image is divided into 46 * 46.

1:Nose, 2:Neck, 3:RShoulder, 4:RElbow, 5:RWrist, 6:LShoulder, 7:LElbow, 8:LWrist, 9:RHip, 10:RKnee, 11:RAnkle, 12:LHip, 13:LKnee, 14:LAnkle, 15:REye, 16:LEye, 17:REar, 18:LEar, 19:Bkg

Define the function to get the position of max of confidence of each body part.

maxpts[img_, confidences_, idex_] := Module[{pos, pts, h},
  pos = Reverse@First@Position[h = confidences[[idex]], Max@h];
  pts = (pos/46)*ImageDimensions@img; 
  pts = {pts[[1]], (ImageDimensions@img)[[2]] - pts[[2]]}
  ]

Connect the detected body parts and show the result together on the original image.

showpose[img_] := Module[{bodylist, size, out, confidences, pts, pose},
  bodylist = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14};
  size = {368, 368};
  out = trainedOpenPose[img];
  confidences = out[[2]];
  pts = maxpts[img, confidences, #] & /@ bodylist;
  pose = Graphics[{
     Yellow, Thickness[.0125], Line[pts[[#]] & /@ {1, 2}],
     Green, Line[pts[[#]] & /@ {2, 3, 4, 5}],
     Cyan, Line[pts[[#]] & /@ {2, 6, 7, 8}],
     Orange, Line[pts[[#]] & /@ {2, 9, 10, 11}],
     Magenta, Line[pts[[#]] & /@ {2, 12, 13, 14}],
     PointSize[Large], Red, Point[pts],
     White, Point[{{0, 0}, ImageDimensions@img}]
     }, ImagePadding -> All];
  Show[img, pose]
  ]

Let' try.

img = Import["ichiro.jpg"];
showpose[img]

enter image description here

Future work

? Estimate the pose of an image in which multi-person are by using PAFs of output1 of OpenPose.

? Convert a more accurate pose estimation model.

Attachments:
openpose.nb
POSTED BY: Kotaro Okazaki
26 Replies
Sort By:

Aaaaand... it works! Thanks so much, Kotaro-San :)

For posterity's sake, here are the things that had to happen to get it working with conda on OSX:

1) Get the right version of python: "conda create -n python3 python=3.7 anaconda"

2) Switch to that python virtualenv: "conda activate python3"

3) Install pytorch for that virtualenv: "conda install pytorch"

4) pqzmq (the python <-> mathematica library) seems to already be installed with the conda distro, but just in case: "conda install pyzmq"

5) Find the path to the conda python install: "which python"

6) Register the conda python with mathematica:

ExternalEvaluate; ExternalEvaluatePrivateresetCache[] RegisterExternalEvaluator["Python", "/opt/anaconda2/envs/python3/bin/python"]

7) Modify Kotaro-San's ExternalEvaluate code to set the directory to the one containing the the .pth file: os.chdir('full path here')

8)I also added a "Normal" to this line of Kotaro-San's code, but I don't know that it was essential: rule = Thread[replacenames -> Normal[parametersReshape]];

That's it. Note that 1-5 are terminal commands, while 6-8 are within Mathematica. Enjoy!
POSTED BY: Jonathan Simon

Kotaro-San,

Thank you so much for the quick reply -- I really appreciate it! I am soooo excited about learning about neural networks and this seems like a terrific opportunity to get into it!

Could you perhaps also let me know what versions of numpy, pkl, and torch you are using? I can certainly switch to a python 3 anaconda package if that will resolve things, but I'd prefer to install all the correct packages this time around :)

Again -- my sincerest appreciation from Chicago, and I hope all is well with you in these difficult times!

Cheers, Jon
POSTED BY: Jonathan Simon

Jonathan-san,

The versions of numpy, pkl, and torch I use are enter image description here
POSTED BY: Kotaro Okazaki

Hi All,

I tried to test out this model, and it failed all over the place :(:( I am wondering if there is a compatibility issue, if links have broken, or something else. To get it to run at all, I first had to make a few changes:

1) "https://www.dropbox.com/s/ae071mfm2qoyc8v/pose_model.pth?\ dl=0" points to posemodel.pth, not posemodelscratch.pth, so I changed the filename in the python ExternalEvaluate[] command sequence to "posemodel.pth" -- is that the wrong model?!

2) I had to register my anaconda 4.8.3 install of python 2.7.16 with mathematica after installing pyzmq; that's my python install that has pytorch installed. The proper external evaluation initialization sequence is now: " ExternalEvaluate ExternalEvaluateImportExportPrivate`$ImporterPythonSession = StartExternalSession["Python" -> "String"] session = StartExternalSession["Python"] "

3) "trainedOpenPose = NetReplacePart[openpose, rule]" fails unless I modify the preceding line to read: rule = Thread[replacenames -> Normal[parametersReshape]]; that is, I have added a "Normal" to strip out the NumericArray[...,"Real32"] commands

At the end everything runs, but the model fails to recognize Ichiro properly, giving only one pair of points that are not even on his body... PLEASE HELP! Thanks!

Attachments:
PoseEstimationTest.nb
POSTED BY: Jonathan Simon

Jonathan-san,

Thank you for your comment. I've evaluated your notebook and my notebook in my new environment(v12.1) and they have recognized Ichiro properly. It may be due to the different versions of Python(2.7.16 vs 3.7.4).

I attached my result of your notebook.

Attachments:
PoseEstimationTest.nb
POSTED BY: Kotaro Okazaki
Wayne Allen
Wayne Allen
Posted 5 years ago

How come I do not know "Person::93r37" where this comes from ???

Entity["Concept", "Person::93r37"]

We are enterprise licensed customers for years and documentation center has nothing on this????
POSTED BY: Wayne Allen
Wayne Allen
Wayne Allen
Posted 5 years ago

Tech support responded to this, therefore no worries.
POSTED BY: Wayne Allen
Wayne Allen
Wayne Allen
Posted 5 years ago

Step 3 takes a long time on my machine, why?
POSTED BY: Wayne Allen

I'm sorry I have no clear answer to your question. However, it takes a few seconds in my environment (Windows 10 and Mathematica v12.0).
POSTED BY: Kotaro Okazaki
Wayne Allen
Wayne Allen
Posted 5 years ago

iMAC 12.0 Mathematica and it hangs for hours.

I am going to submit this to tech support.
POSTED BY: Wayne Allen
Wayne Allen
Wayne Allen
Posted 5 years ago

Wolfram techsupport wrote and asked me to ask you Mr.Okazaki to send me your FULL NOTEBOOK to run your code. They like to use that notebook to track the problem.

Let me know if you are willing to do that

Dara

POSTED BY: Wayne Allen

Allen-san,

I have attached my notebook to the post. It takes about one and a half minutes in my environment. Please make sure.

Your problem may be a problem with indentation in ExternalEvaluate.

I hope this will help.
POSTED BY: Kotaro Okazaki
Wayne Allen
Wayne Allen
Posted 5 years ago

Thank you Sir!

ExternalEvaluate [ ] has an issue with Python Numpy version so little odd thingy like that.

POSTED BY: Wayne Allen

I saw this post, but don't see any links to OpenPose itself. Is it a Wolfram toolset? Or is there a GitHub repository? Any links would be appreciated.
POSTED BY: David Whitten

David-san,

Thank you for your comment. I refered here.
POSTED BY: Kotaro Okazaki
Julian Francis
Julian Francis
Posted 5 years ago

Coincidentally I was also looking at converting OpenPose when I came across this post. This is lovely work, thank you very much. It'd be great to see it in the Wolfram Neural Net Repository. I have had 3 models (single shot detectors) submitted and accepted (several more in the pipeline). I don't work for Wolfram, but they were very helpful guiding me through their submission process and they do acknowledge your contribution on their repository site.

Thanks once again,

Julian.
POSTED BY: Julian Francis
Test Account
Test Account
Posted 5 years ago

Julian,

Thank you for your kind words. As always, it is a pleasure working with you to get your models in the repository. We always look forward to more submissions from you, Kotaro-san and all our users.

Thanks, Tuseeta
POSTED BY: Test Account

As a somewhat simplistic way of finding multiple poses in an image, I thought it would be interesting to use ImageContents to find people and then use your OpenPose implementation to detect poses for each person.

First, I altered your showPose function to include an origin parameter and removed the last line to make it return the poses only (i.e. a pose function):

pose[img_, origin_: {0, 0}] := 
 Module[{bodylist, size, out, confidences, pts, people, pose},
  bodylist = Range[14];
  size = {368, 368};
  out = trainedOpenPose[img];
  confidences = out[[2]];
  pts = Map[Plus[origin, #] &, 
    maxpts[img, confidences, #] & /@ bodylist];
  pose = Graphics[{Yellow, Thickness[.0125], 
     Line[pts[[#]] & /@ {1, 2}], Green, 
     Line[pts[[#]] & /@ {2, 3, 4, 5}], Cyan, 
     Line[pts[[#]] & /@ {2, 6, 7, 8}], Orange, 
     Line[pts[[#]] & /@ {2, 9, 10, 11}], Magenta, 
     Line[pts[[#]] & /@ {2, 12, 13, 14}], PointSize[Large], Red, 
     Point[pts]}, ImagePadding -> All]]

Then I made a function that retrieves the images and bounding boxes for each person in the original image, computing and translating poses for each image based on the origin of its bounding box:

multiPose[img_] := Module[{people, boxes, poses},
  {people, boxes} = 
   Transpose[
    Normal@ImageContents[img, 
        Entity["Concept", "Person::93r37"]][[All, {"Image", 
         "BoundingBox"}]] // Values];
  poses = 
   Table[pose[people[[i]], boxes[[i, 1]]], {i, Length[people]}]]

Finally, a function to show the poses in context:

showMultiPose[img_] := Show[img, Sequence[multiPose[img]]]

Not suitable for real-time processing or anything, but it was very easy to implement, and it seems to work in seconds, even for a decent number of people:

(From Google search results for

POSTED BY: Brian Wood

Brian-san,

Thanks for your try. Your idea of using ImageContents to estimate multi-person pose is really great. It was unthinkable to me. I think the best part of the community is knowing how to use Wolfram Language inconceivably. Thank you again!

POSTED BY: Kotaro Okazaki

That was very informative, thank you.
POSTED BY: Eleazar Johannian

This is a great example; thank you for the post! I can imagine all sorts of interesting uses for OpenPose in the Wolfram Language.

I was trying to replicate your process, and I got stuck on the last part of Step 4, which I think may be missing a line of code:

Reshape each one-dimensional list of parameters to the dimension of the corresponding weight or bias.

The subsequent step uses a parametersReshape variable, which is probably meant to be defined here. Could you possibly provide this missing piece?

I'm looking forward to exploring this further!
POSTED BY: Brian Wood

Brian-san,

Thank you very much for taking the time and spotting this. Sorry I have updated my post. There was lines of code missing. 

getDimB[layer_] := Dimensions@NetExtract[layer, "Biases"]
getDimW[layer_] := Dimensions@NetExtract[layer, "Weights"]
convs = NetExtract[NetInitialize[openpose], #] & /@ convlayerpos;
dimW = getDimW /@ convs;
dimB = getDimB /@ convs;
dim = Flatten[Transpose[{dimW, dimB}], 1];
parametersReshape = MapThread[ArrayReshape, {parameters, dim}];
POSTED BY: Kotaro Okazaki

Kotaro-san,

Thank you for the update. That was exactly the detail I needed! Looks like your implementation is working perfectly for me.
POSTED BY: Brian Wood

Kotaro-san, what a wonderful work and presentation, thank you for sharing!

POSTED BY: Vitaliy Kaurov

enter image description here - Congratulations! This post is now featured in our Staff Pick column as distinguished by a badge on your profile of a Featured Contributor! Thank you, keep it coming!

POSTED BY: EDITORIAL BOARD
Test Account
Test Account
Posted 5 years ago

It is wonderful to see how you converted this model and so soon. Please feel free to reach out to us via the contact us button in the Neural Repo page.
POSTED BY: Test Account
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract