
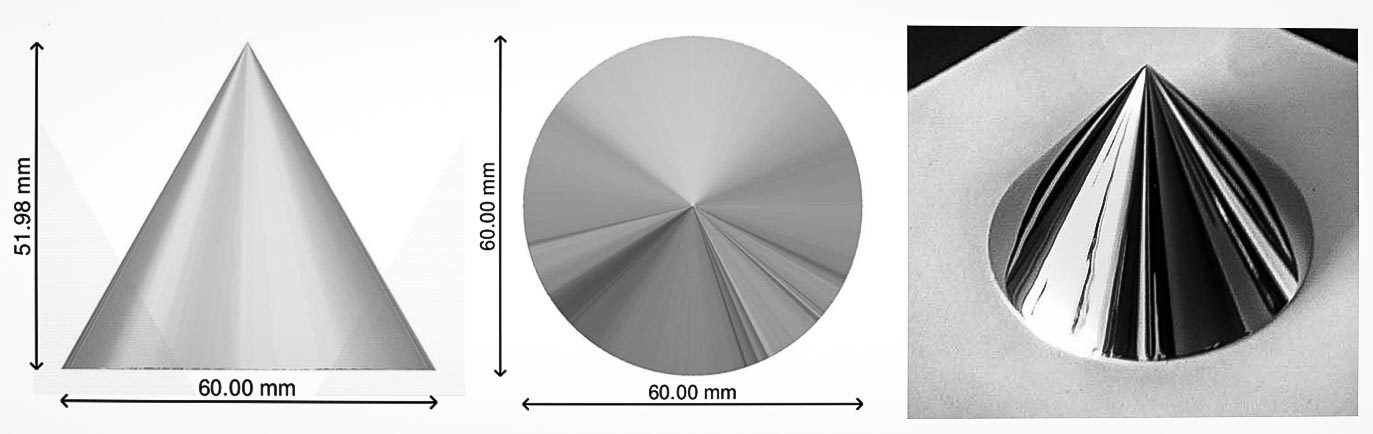
I took the chrome plated conical mirror used in my previous Wolfram Community contribution, suspended it upside down, and asked myself the (anamorphism) question : what should a (deformed) image look like to be reflected in this mirror as the (undeformed) original? We can use Mathematica to solve this problem!
1. Geometry of reflection in a hanging conical mirror 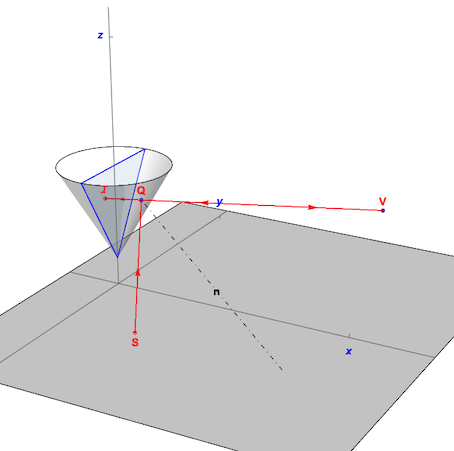
An observer looking from a viewpoint at V in the direction of the cone, will see the point S reflected as the point I. Q is the intersection point of the view line VI with the cone. This function computes this intersection:
viewlineConeIntersection[{yi_, zi_}, {xv_, zv_}, h0_, h_] :=
Module[{t1, t2},
t1 = Sqrt[-h^2 xv^2 yi^2 + h0^2 (xv^2 + yi^2) + xv^2 zi^2 +
yi^2 zv^2 - 2 h0 (xv^2 zi + yi^2 zv)];
t2 = 1/(h^2 (xv^2 + yi^2) - (zi - zv)^2);
{t2 xv ((h0 - zi) (zi - zv) + h (h yi^2 + t1)),
t2 yi (h^2 xv^2 + (h0 - zv) (-zi + zv) - h t1),
t2 (-h0 (zi - zv)^2 + h^2 (xv^2 zi + yi^2 zv) + h (-zi + zv) t1)}]
With the help of viewlineConeIntersection, the following function computes the intersection of the reflection line IQ with the x-y plane. This intersection is the anamorphic map of I.
hangingConeAnamorphicMap[{yi_, zi_}, {xv_, zv_}, h0_, h_] :=
Quiet[Module[{mirror, ptI, ptV, imageTriangle, vwLine, xq, yq, zq,
ptQ, xn, yn, zn, ptVr},
mirror = Cone[{{0, 0, h0 + h}, {0, 0, h0}}, 1]; ptI = {0, yi, zi};
ptV = {xv, 0, zv};
imageTriangle =
Triangle[{{0, 0, h0}, {0, -1, h + h0 - .001}, {0, 1,
h + h0 - .001}}];
If[! RegionMember[imageTriangle, {0, yi, zi}], {yi, zi} =
Rest[RegionNearest[imageTriangle, {0, yi, zi}]], {yi, zi}];
vwLine = Line[{ptI, ptV}]; {xq, yq, zq} =
viewlineConeIntersection[{yi, zi}, {xv, zv}, h0, h];
ptQ = {xq, yq, zq}; {xn, yn} = Normalize[{xq, yq}];
zn = -Sin[ArcTan[1/h]];
ptVr = ReflectionTransform[{xn, yn, zn}, ptQ][ptV];
Solve[{{x, y, z} \[Element] HalfLine[{ptVr, ptQ}] && z == 0}, {x,
y, z}][[1, All, -1]]]]
This is the function in action as the pointS follows the anamorphic map of a reflected circle:
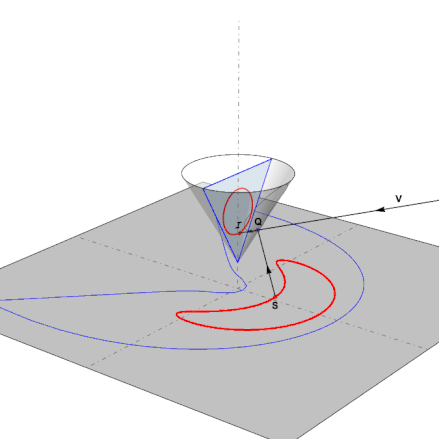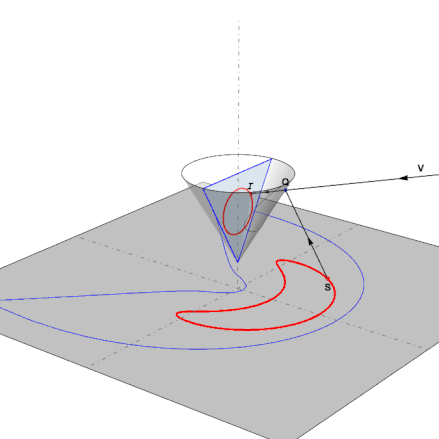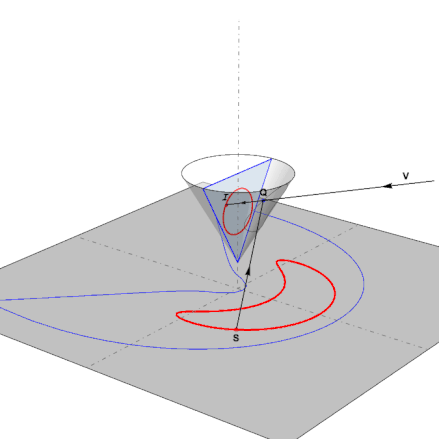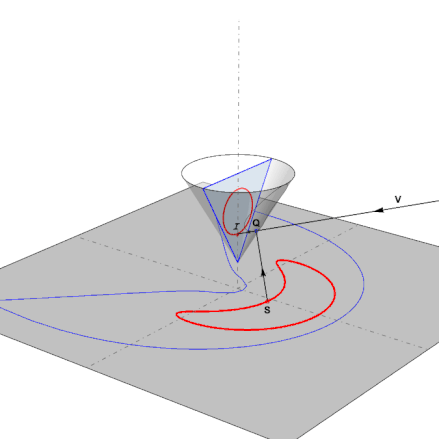
2. Preparing the images
It is clear that the points I all will have to belong to the triangular region Triangle[{{-1,51.98/30},{1,51.98/30},{0,0}}]. The following code computes the function range staring from its triangular domain.
Module[{xv = 5., zv = 3., r = 1, h = 51.98/30, h0 = .5, triangle,
circlePts, anaCirclePts, trianglePts, anaTrianglePts},
triangle = Triangle[{{-h0 - .02, 0}, {-h0 - h, 1}, {-h0 - h, -1}}];
trianglePts =
DeleteDuplicates[
RegionNearest[triangle,
CirclePoints[{0, (h0 + h)/2}, 4, 1000]] /. {x_?NumericQ,
y_} :> {y, -x}];
anaTrianglePts =
DeleteCases[
ParallelMap[Most[hangingConeAnamorphicMap[#1, {xv, zv}, h0, h]] &,
trianglePts], {}];
Grid[{Style[#, Bold, 14] & /@ {"Domain", "Range"}, {Rotate[
Graphics[{HatchFilling[], FaceForm[LightGray],
EdgeForm[AbsoluteThickness[1.5]], triangle},
PlotRange -> {{-4, 2}, {-2, 2}}, Axes -> True,
TicksStyle -> Small, ImageSize -> 400], -Pi/2],
Rotate[Graphics[{HatchFilling[], FaceForm[LightGray],
EdgeForm[AbsoluteThickness[1.5]], FaceForm[Lighter[Gray, .85]],
Polygon[anaTrianglePts]},
PlotRange -> {{-4, 2.5}, {-4.5, 4.5}}, Axes -> True,
TicksStyle -> Small, ImageSize -> 300], -Pi/2]}}]]
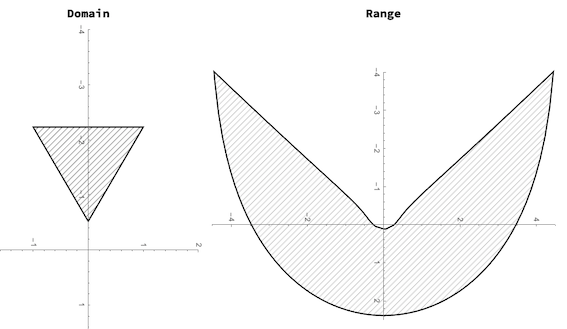
The reflection appearing in the inverted cone will maximum be triangular in shape or at least fit inside a triangle. In our case (we suspend the cone with its tip at .5 above the x-y plane), this is the triangle Triangle[{{-1,51.98/30},{1,51.98/30},{0,0}}]:
Graphics[{EdgeForm[Black], HatchFilling[], FaceForm[LightGray],
Triangle[{{-1, 51.98/30}, {1, 51.98/30}, {0, 0}}] /. {x_?NumericQ,
y_} :> {x, y + 0.5}}, Axes -> True, AxesOrigin -> {0, 0}]
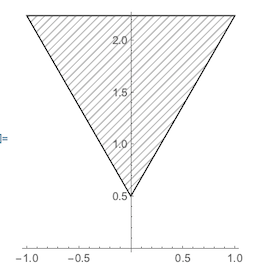
In order to fit an image inside this triangle, we need a function that convert the image to a set of colored polygons that fit into the triangle (or other) region.
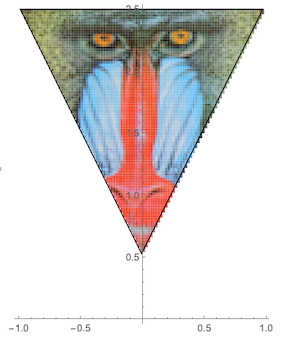
Module[{mandrill, irc},
mandrill = ImageResize[ExampleData[{"TestImage", "Mandrill"}], 100];
irc = imageRegionCrop[mandrill,
Region@Triangle[{{-.99, 1}, {.97, 1}, {-.01, -.97}}]];
Graphics[{irc /. {x_?NumericQ, y_} :> {x, y + 1.5}, FaceForm[],
EdgeForm[Black],
Triangle[{{-.99, 1}, {.97, 1}, {-.01, -.97}}] /. {x_?NumericQ,
y_} :> {x, y + 1.5}}, Axes -> True,
AxesOrigin -> {0, 0} Axes -> True, AxesOrigin -> {0, 0}]]
3. 3D simulation in Mathematica
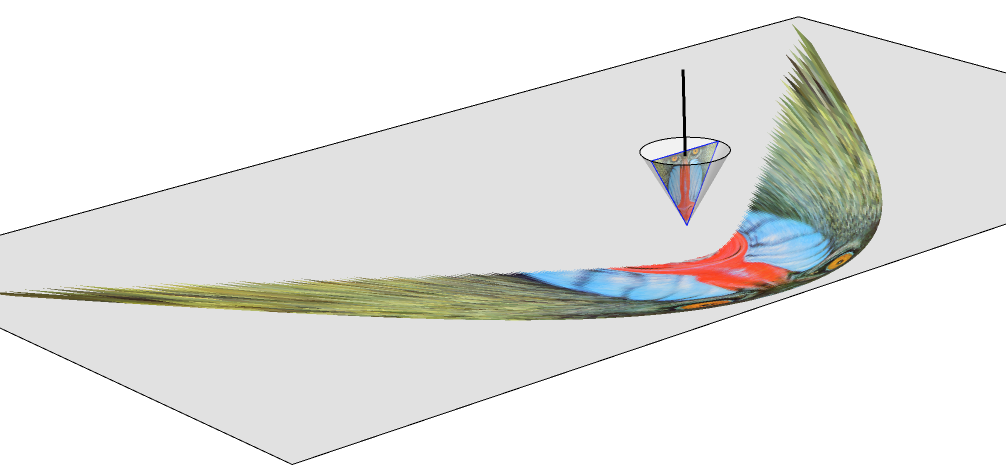
Now, we convert the triangular set of colored polygons into its anamorphic map with our function hangingConeAnamorphicMap. With Graphics3D, we can see a simulation of how the anamorphic image will look reflected in the hanging cone:
Module[{r = 1., h = 51.98/30, h0 = .5, xv = 5, zv = 3.5, mirrorCone,
ptV, imageTriangle, img, splitLogo, pixelPolys, anaPolys},
mirrorCone = Cone[{{0, 0, h0 + h}, {0, 0, h0}}, r];
ptV = {xv, 0, zv};
imageTriangle =
Triangle[{{0, 0, h0}, {0, -r, h + h0}, {0, r, h + h0}}];
img = ImageResize[ExampleData[{"TestImage", "Mandrill"}], 200];
splitLogo =
imageRegionCrop[img,
Triangle[{{-1, 51.98/30/2.}, {1,
51.98/30/2.}, {0, -51.98/30/2.}}]];
pixelPolys = splitLogo /. {x_?NumericQ, y_} :> {x, y + 1.5};
anaPolys =
DeleteCases[
MapAt[hangingConeAnamorphicMap[#, {5, 1.367}, .5, 51.98/30] &,
pixelPolys, {All, -1, All, All}] /. {x_?NumericQ, y_, z_} :> {x,
y}, {z == 0}, \[Infinity]];
Graphics3D[{{LightGray,
InfinitePlane[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}}]},
{Opacity[.35], LightGray, Specularity[1, 2],
mirrorCone}, {AbsoluteThickness[2],
Line[{{0, 0, h + h0 + 2}, {0, 0, h + h0}}], AbsolutePointSize[3],
Point[{0, 0, h + h0 + 22}]},
{FaceForm[], EdgeForm[{Blue, AbsoluteThickness[.5]}],
imageTriangle},
pixelPolys /. {y_, z_} :> {0, y, z},
anaPolys /. {x_?NumericQ, y_} :> {x, y, 0.001}}]]
5. Real world testing
To test this in a real world setting, we need a printout of the anamorphic image...
Graphics[{{Thin, Circle[]}, anaPolys}]

...locate the printout under our hanging conical mirror....

...and see the result reflected as the original and undeformed image!
