Take a word and find its synonyms. Then find the synonyms of the synonyms from the previous step. And so on.
For how long will the number of synonyms continue to grow?Language structures can take peculiar shapes. Code can be quite simple to compute and automate informative visualizations. Below vertex size is larger if the vertex has more connections, meaning a word has a greater number of synonyms. Note GraphLayout -> {"BalloonEmbedding", "RootVertex" -> word} option to Graph is used to produce this specific layout. The code below is based on
an example from Documentation.
Lets define a function:
SynonymNetwork[word_String, depth_Integer, labels_: Tooltip] :=
Module[{ed, sz, g},
(* list of edges *)
ed = Union[Sort /@ Flatten[Rest[NestList[Union[Flatten[
Thread[# <-> WordData[#, "Synonyms", "List"]] & /@ #[[All, 2]]]] &, {"" <-> word}, depth]]]];
(* size of vertices based on number of synonyms *)
sz = Thread[VertexList[Graph[ed]] -> Map[{"Scaled", #} &,
.05 (.01 + .99 N[Rescale[VertexDegree[g = Graph[ed]]]])^.5]];
(* graph *)
SetProperty[g,
{GraphLayout -> {"BalloonEmbedding", "RootVertex" -> word},
EdgeStyle -> Directive[Opacity[.2], Red],
VertexStyle -> Directive[Opacity[.1], Black],
VertexStyle -> {word -> Directive[Opacity[1], Red]},
VertexSize -> sz, VertexLabels -> Placed["Name", labels]}]
]
Here how it works:
SynonymNetwork["promise", 3]
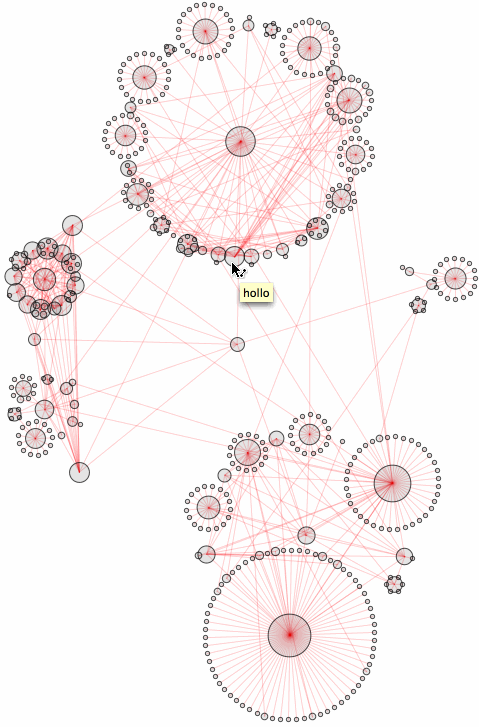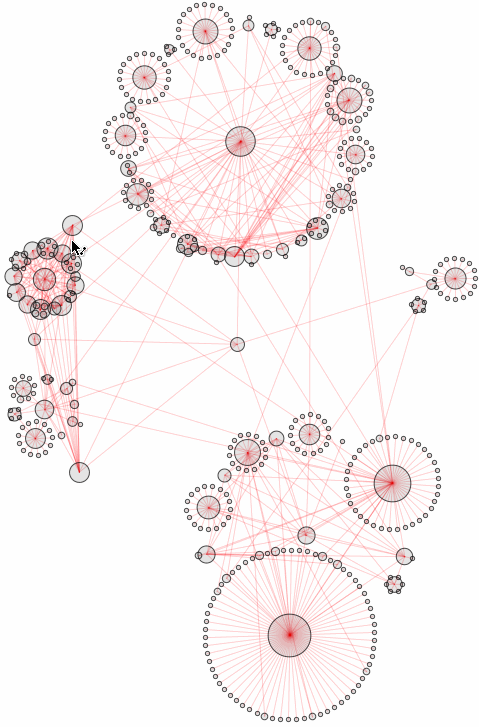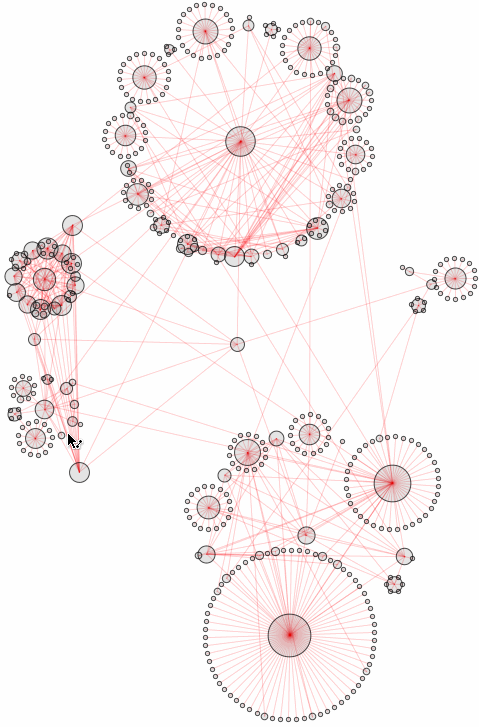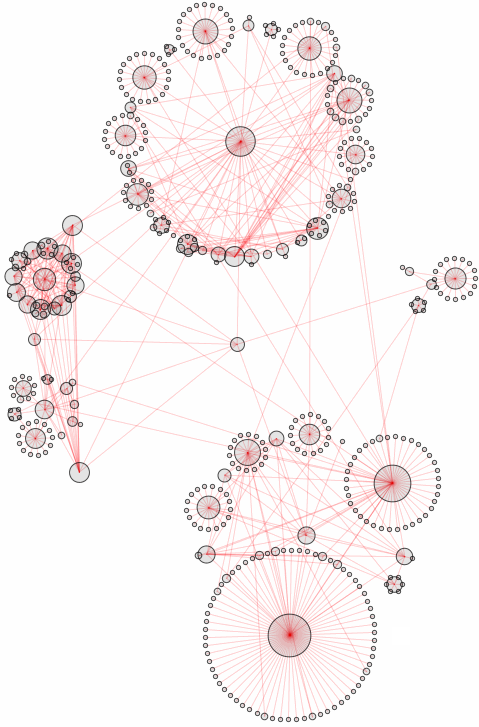
Now as I asked earlier: will the number of synonyms continue to grow? This of course depends on a particular thesaurus dictionary at hand. But once we settled on one, what can we find? Obviously some very specific words have no synonyms at all:
In[1]:= WordData["transmogrification", "Definitions"]
Out[1]= {{"transmogrification", "Noun"} ->
"the act of changing into a different form or appearance (especially a fantastic or grotesque one)"}
In[2]:= WordData["transmogrification", "Synonyms"]
Out[2]= {{"transmogrification", "Noun"} -> {}}
Some words will have very trivial small finite networks (note network depth is set 20, while even 100 or greater will not change it):
SynonymNetwork["chemistry", 20, Above]
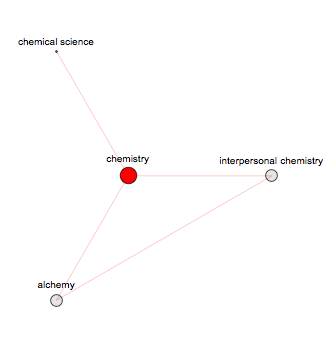
And of course many words will have networks that grow very fast. This applies not only for very general words such as fast or beautiful, but also for strange rare words such as "discombobulate":
ParallelMap[Length[EdgeList[SynonymNetwork["discombobulate", #]]] &, Range[16]]
Out[]= {9, 97, 1097, 7644, 26051, 46671, 59440, 65187, 67805, 68798, 69274, 69456, 69565, 69587, 69592, 69592}
data = ParallelMap[Length[VertexList[SynonymNetwork["discombobulate", #]]] &, Range[16]
{10, 73, 787, 4293, 11646, 18858, 22931, 24911, 25743, 26096, 26238, 26302, 26321, 26330, 26330, 26330}
ListPlot[data, Filling -> Bottom, Joined -> True, Mesh -> All, AxesLabel -> {"Network depth", "Synonyms"}]
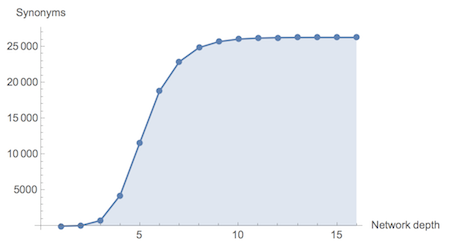
So we see
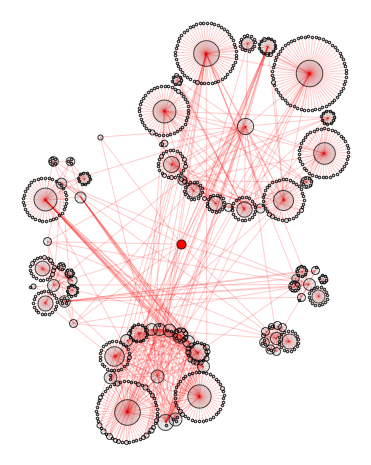
"discombobulate" synonym network gets saturated at depth 15 and attains 26330 vertices and 69592 edges. Quite magnificent result I think ;-) This is, btw, very inefficient way of computing the convergence we repeat same computations many times while building the graph. Ideally we should introduce counting synonyms part into our SynonymNetwork function. This is how discombobulate network looks "big" already at depth 3:
SynonymNetwork["discombobulate", 3]
How big do such networks get? Can we make some estimates? Well, lets first define set of all words that to belong to discombobulate network:
gr = SynonymNetwork["discombobulate", 15];
ver = VertexList[gr];
Then lets find all unique words in Alice in Wonderland:
alice = Union[ToLowerCase[StringSplit[ExampleData[{"Text", "AliceInWonderland"}], RegularExpression["[\\W_]+"]]]];
alice // Length
Out[]= 1484
Then select, say, only nouns that have synonyms
nouns = Select[alice, MemberQ[WordData[#, "PartsOfSpeech"], "Noun"] && WordData[#, "Synonyms", "List"] =!= {} &];
nouns // Length
Out[]= 809
We see that more than half of these nouns belong to the discombobulate network:
MemberQ[ver, #] & /@ nouns // Tally
Out[]= {{False, 223}, {True, 586}}
I also would like to share some beautiful smaller CONVERGED (saturated) networks, which I found, - beautiful in structure and sets of words they gather (see below). They of course do not belong to huge "discombobulate" graph above. And as already mentioned I propose the following - comment if:
- you find some beautiful networks
- you can figure out how we can make estimates on large networks or do any further digging
- you can optimize code
- you have any ideas / comments at all ;-)
===> "dragonfly" - 23 synonyms, depth 3ParallelMap[Length[VertexList[SynonymNetwork["dragonfly", #]]] &, Range[7]]
Out[]= {8, 14, 23, 23}
SynonymNetwork["dragonfly", 20, Above]
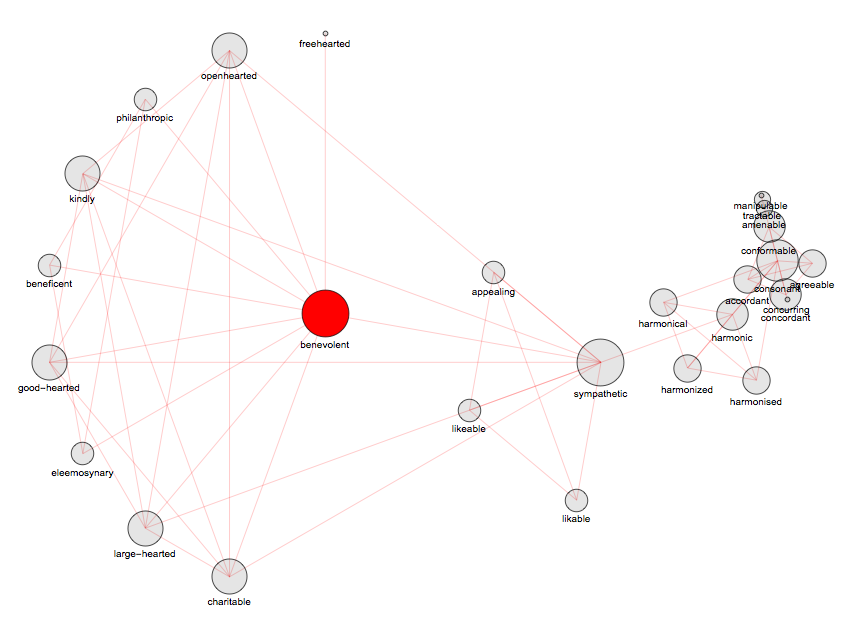
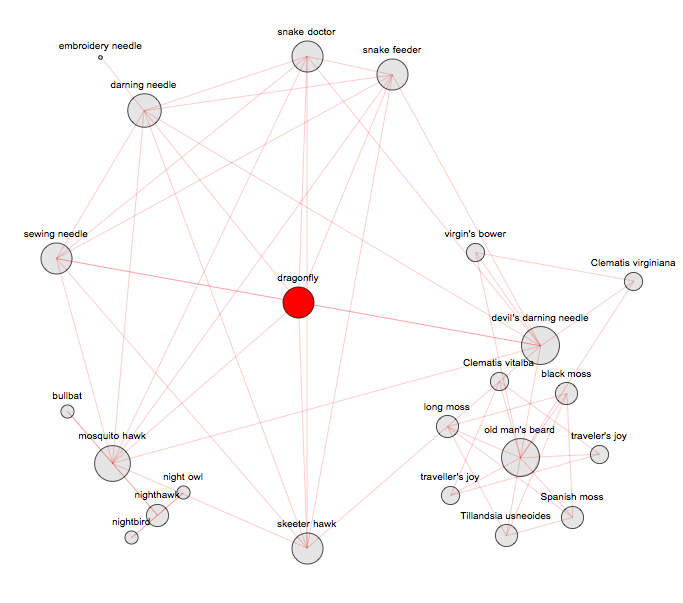===> "benevolent" - 27 synonyms, depth 7ParallelMap[Length[VertexList[SynonymNetwork["benevolent", #]]] &, Range[9]]
Out[]= {11, 15, 19, 23, 25, 26, 27, 27}
SynonymNetwork["benevolent", 20, Below]
