WHUPS! Obsolete even as I posted it...

Also 18:

dat = FoldList[PolyhedronFaceReflect, a4,
       {3, 1, 5, 2, 1, 2, 5, 2, 3, 5, 1, 3, 2, 1, 2, 3, 2}];
    Graphics3D[{dat, Red, dat[[1]]}, Boxed -> False]

14 and closer to a ring, but fails because of overlap:

dat = FoldList[PolyhedronFaceReflect, a4,
   {3, 1, 5, 2, 5, 1, 3, 5, 1, 3, 2, 3, 1}];
Graphics3D[{dat, Red, dat[[1]]}, Boxed -> False]

Hmm... Found another ring of 18:

dat = FoldList[PolyhedronFaceReflect, a4,
   {3, 1, 2, 3, 5, 2, 1, 5, 2, 5, 1, 2, 5, 3, 2, 1, 3}];
Graphics3D[{dat, Red, dat[[1]]}, Boxed -> False]

(The "Red" lets me keep track of my starting point.)

Ah: So that ends the story!! Back to the tetrahedron problem: That problem arose b/c it is quite simple to make perfect closed loops from cube, octahedron, dodecahedron, icosahedron. I have little models of those 4 here. So what you have discovered is that the same is true for your anti prism. But what is interesting is that it is nontrivial compared to the Platonic ones. Of course, maybe there is a simpler loop.... But finding what you found is great! Congrats. (Maybe even publishable. Oh wait: Why don't mwe make it an American Math Monthly problem. I am now the Proposal editor for the Amer Math Monthly, so I decide what we accept. This looks like a great problem! (Ie, True or False: there is an embedded chain of antiprisms) . Embedded means no intersections. One delicate point is that AMM Problems should not be published elsewhere. Maybe in a year or so you could remove the answer that is posted here.

Searching for strings such as your 2,3,5,1 etc. is exactly how we came up with very small errors in the tetrahedral case. We used some symmetry and palindromicity and automated it all (checking for non-intersections: highly non-trivial to automate that) and got error down to 10^-18. That sort of approach would likely work here.

But the real excitement came when we were more organized...and stumbled across a quite simple shape that led to error below any pre-assigned epsilon. That was very satisfying indeed. As to how that might work for these antiprisms I can't predict, but it is worthy of investigation.

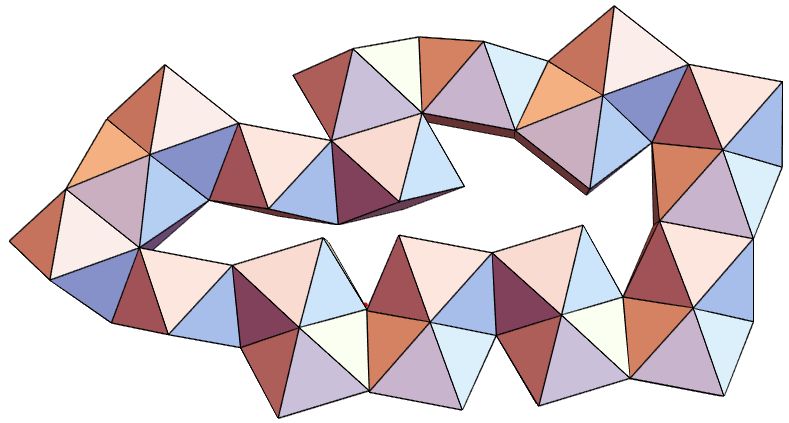
Quite a few have asked ... "So how close is this?"

First, a slightly simpler antiprism:

root = Root[-1 + 2 #^4& , 2, 0];
v = {{1, -1, -root}, {-1, -1, -root}, {-1, 1, -root}, {1, 
    1, -root}, {Sqrt[2], 0, root}, {0, Sqrt[2], root}, {-Sqrt[2], 0, 
    root}, {0, -Sqrt[2], root}};
f = {{1, 2, 3, 4}, {5, 6, 7, 8}, {1, 8, 2}, {2, 7, 3}, {3, 6, 4}, {4, 
    5, 1}, {1, 5, 8}, {2, 8, 7}, {3, 7, 6}, {4, 6, 5}};
a4 = Polyhedron[v, f];

Next, a new function, PolyhedronFaceReflect, that refects the polyhedron on a given face:

PolyhedronFaceReflect[poly_, face_] := 
 Module[{v = poly[[1]], f = poly[[2]]},
  Polyhedron[
   RootReduce[
    ResourceFunction["ReflectPoints"][v[[Take[f[[face]], 3]]], v]], 
   f]]

With that, we can reflect on the faces and see the gap when the polyhedron is reflected precisely. A red sphere has been added to draw attention to the gap area.

dat = FoldList[PolyhedronFaceReflect, 
   a4, {3, 5, 3, 5, 3, 5, 3, 5, 3, 5, 3, 5}];
Graphics3D[{{Red, Sphere[v[[6]] + {0, 0, .1}, .05]}, dat}, 
 Boxed -> False]

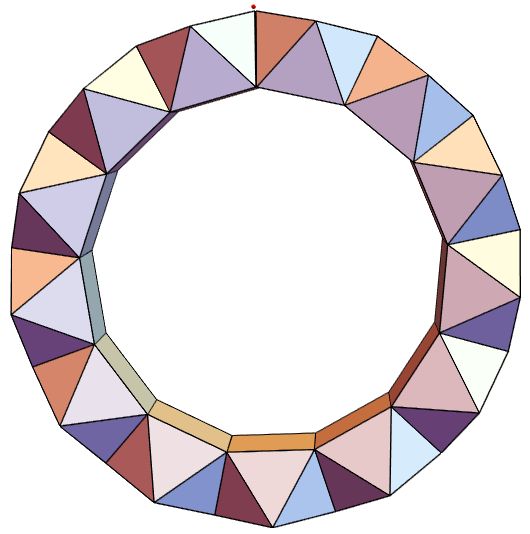
How far apart are the points in the gap triangles, for length 2 edges? 0.0268171 or 0.0189626

N[EuclideanDistance[dat[[1, 1, 6]], dat[[13, 1, 8]]]]
N[EuclideanDistance[dat[[1, 1, 3]], dat[[13, 1, 2]]]]

The gap is small enough that it's hard to draw attention to it. Here's a more twisted ring with a gap of 0.0330049:

dat = FoldList[PolyhedronFaceReflect, a4,{2,3,5,1,2,5,3,1,5,3,2,5,2,1,2,5,2,3,2}];
Graphics3D[{{Red,Sphere[v[[6]]+{0,0,.1},.05]},dat}, Boxed-> False]
N[EuclideanDistance[dat[[1, 1, 4]], dat[[20, 1, 4]]]]

@Ed, nice! This is so asking for 3D printing :-) like it was done with @Stan's tetrahedral chain challenge post. I could not resist generating GiF animation showing 3D view of the figure and the effect of offset constant. I added it to Ed's post. Here is the code:

frame=
ParallelTable[

offset=#+{0,0,Sqrt[1-1/4 Sec[Pi/8]^2]+4.05+2*Sin[3(u-Pi/2)]^2}&/@
(2PolyhedronData[{"Antiprism",4},"VertexCoordinates"]);

Graphics3D[Table[GraphicsComplex[RotationMatrix[k 2 Pi/13,{0,1,0}].#&/@offset,Polygon/@face],{k,0,12}],
Boxed->False,SphericalRegion->True,SphericalRegion->True,ImageSize->250,ViewPoint->7{.3,Sin[u],Cos[u/2]}],

{u,Pi/2,4 Pi+Pi/2,.1}];

Export["antiptism4.gif",frame]

Wow. I wonder who asked this and when... I guess the first question is: Prove that perfection is not possible. For regular tetrahedra that was done in 1958.

Next question -- perhaps open -- can this be done to get error under any positive epsilon? I and M Elgersma did this for regular tetrahedra a few years ago.

To clarify, I would not change the 4-antiprism to an n-antiprism (just yet). Focus just on the 4-antiprism and the same questions that were asked years ago of the regular tetrahedron.

1. Is it possible to make a chain of 4-antiprisms that do not intersect and close up perfectly. NO for the tetrahedron (1958).

2. Assuming the answer to 1 is NO (a proof would likely be similar to the not-too-hard 1958 proof, which was based on barycentric coordinates, can one find, for any positive epsilon, an imbedded chain that has error epsilon in terms of how close it is to closing up. (YES for tetrahedron, Elgesma and Wagon, 2017 or so)

IF anyone wants copies of papers or more details on the 1958 proof, just ask me by usual email. I am easy to find: see stanwagon.com