Both on the internet by the artist Jonty Hurwitz (left) and in my previous community contribution (middle and right) , we see how a properly computed and deformed anamorphic object reflects as the realistic original in a cylindrical mirror.

In this contribution, I want to show that similar reflected images and videos can be created starting from 2D images i.o. 3D printed objects.
An alternative way to apply custom made transformations to images is to convert the image to a GraphicsComplex with the function ImageGraphics and apply the transformation to the point coordinates in the GraphicsComplex.
The transformation I will use is the function cylAnamorphMapCF from my previous contribution about anamorphism. The function computes the coordinates of a point in the x-y plane that, seen from the viewpoint pntV, will be reflected as an image point pntI in a vertical cylinder of radius 1.
cylAnamorphMapCF = Compile[{{pntI, _Real, 1}, {pntV, _Real, 1}},
Quiet@Module[{yi, zi, xv, zv, t1, t2, t3}, {yi, zi} = pntI;
{xv, zv} = pntV;
t1 = Sqrt[2 + 1/xv^2 + yi^2 - xv^2 (-1 + yi^2)];
t2 = 2 + yi^2 + 1/xv^2 + xv^2;
t3 = (1 + 2 xv^2 + yi^2 xv^2 + xv^4);
Re[{yi (xv^2 (-1 + xv^2 - t1) t3 + (-1 - xv^2 (2 + 2 t1 + yi^2) +
xv^4 (-1 + 2 t1 + 2 yi^2)) (zv +
xv^2 zv (-1 + t1 + yi^2) +
xv^2 (3 + xv^2 - t1) zi)/(zv - zi))/
t3^2, (-t1/xv + xv (t1 + yi^2))/
t2 - (-1 +
xv^2 (-1 + xv^2 +
xv^4 + (-1 - 2 xv^4 +
xv^2 (3 + 2 t1)) yi^2)) (zi - (-1 + 1/xv^2 + t1 +
yi^2) (-zv + zi)/t2)/(xv t3 (-zv + zi))}]]];
Let us start with a home-made graphic and video of a spinning dollar coin. The function imgrCoin creates a 2D GraphicsComplex of the image using ImageGraphics. This graphics object can then be used as one step in an animation:
First[First[
ImportString[
ExportString[Style["$", FontSize -> 24, FontFamily -> "Times"],
"PDF"], {"PDF", "PageGraphics"}, "TextMode" -> "Outlines"]]];
dollar =
Polygon /@
MapAt[Prepend[# /. {x_, y_} -> {x - 4.5, y - 10.5}/
10, .101] &, %, {2, 1, -1, -1, All, All}][[-1, 1, -1, -1]];
First[First[
ImportString[
ExportString[Style["1", FontSize -> 24, FontFamily -> "Times"],
"PDF"], {"PDF", "PageGraphics"}, "TextMode" -> "Outlines"]]];
one = Polygon@
MapAt[Prepend[# /. {x_, y_} -> {-x + 4.5, y - 10.5}/
10, -.101] &, %, {2, 1, -1, -1, All, All}][[-1, 1, -1, -1]]
imgrCoin[i_] :=
Delete[First[
ImageGraphics[
ImageReflect[
Image@Graphics3D[{EdgeForm[AbsoluteThickness[2]],
FaceForm[Blue], Cylinder[{{-.1, 0, 0}, {0, 0, 0}}, 1],
FaceForm[Red], Cylinder[{{0, 0, 0}, {.1, 0, 0}}, 1],
FaceForm[Gray],
Cylinder[{{-.09, 0, 0}, {.09, 0, 0}},
1.02], {EdgeForm[AbsoluteThickness[2]],
Polygon[Append[#, -1.01] & /@
CirclePoints[100]]}, {AbsoluteThickness[3], Cyan,
one /. {x_?NumericQ, y_, z_} -> {x - .001, y,
z}}, {AbsoluteThickness[3], White, dollar, Red,
Rest[dollar] /. {x_?NumericQ, y_, z_} -> {x + .001, y, z}}},
Boxed -> False, PlotRange -> 1.1,
ViewVector -> 100 {Cos[i Pi/20], Sin[i Pi/20], .15}], Left],
7] /. {x_?(And[NumericQ[#], Not[IntegerQ[#]]] &),
y_} :> {x - 540, y - 250}/420], {2, 1}]
Animate[Graphics[{AbsoluteThickness[4], imgrCoin[i]},
PlotRange -> {{-1, 1}, {-.2, 1.5}}], {i, 40}]

We can now apply our function cylAnamorphMapCF to the coordinates of the GraphicsComplex and make frames for a Video of the anamorphic images:
anaCoinFrames =
ParallelTable[
Graphics[{{Dashed, Circle[]}, AbsoluteThickness[4],
MapAt[cylAnamorphMapCF[#, {10., 10.}] &, imgrCoin[i], {1, All}]},
PlotRange -> {{-3, 3}, {-1, 5}}], {i, 40}];
anaCoinVideo =
Video[VideoTimeStretch[FrameListVideo[anaCoinFrames], 2],
RasterSize -> 200]

The video can then be run on an iPad. The cylindrical mirror on top shows a reflection of the original spinning coin video.

The same procedure can be used starting with an image from the internet. This is a 3D spitfire model from Turbosquid composed of 3,586 triangles: (file "spitfire.obj" attached).
spitfirePolys =
Import[ "/.../spitfire.obj",
"PolygonObjects"] /. {x_?NumericQ, y_?NumericQ,
z_} :> {z + 10, x + .7, y}/5.;
We can write a function imgrSpifire similar to imgrCoin above. This function will create a GraphicsComplex from the imported triangles as seen from the view angle i Pi/20:

We can again apply the function cylAnamorphMapCF to the 17,469 2D coordinates of the the GraphicsComplex and make frames for a list of 40 anamorphic images for a video:
anaSpitfireFrames =
Quiet@ParallelTable[
Graphics[{{AbsoluteThickness[1], Dashed, Circle[]},
AbsoluteThickness[4],
MapAt[cylAnamorphMapCF[#, {10., 8.}] &,
imgrSpifire[i], {1, All}]},(*Axes->True,*)
PlotRange -> {{-4, 4}, {-1.5, 4.5}}], {i, 0, 39, 1}];
anaSpitfireVideo =
VideoTimeStretch[FrameListVideo[anaSpitfireFrames], 2]
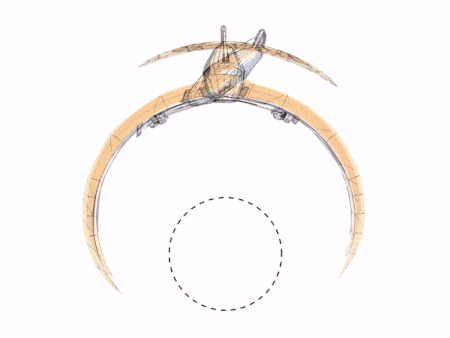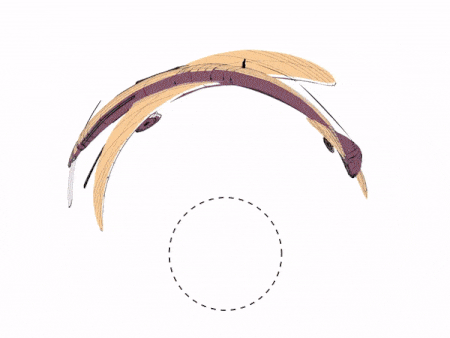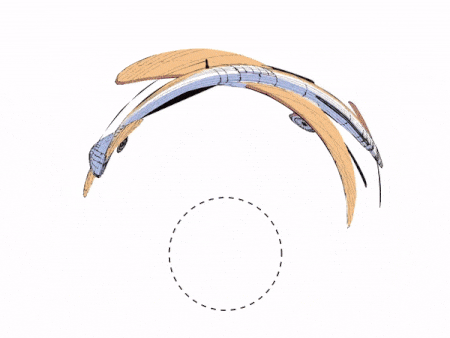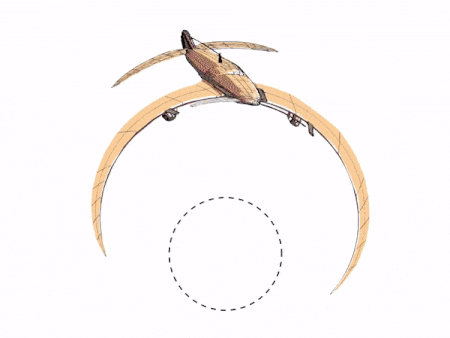
This is how the reflection looks like in a cylindrical mirror on top of an iPad running the above video:

Up now to a more complicated example. We import an STL file of a human head from 3D Model Marketplace CGTrader:
See the attached file: "male face 1.STL". The extracted "PolygonObjects" is a list of 34,496 triangles.
largeHeadPolys = Import[ "/.../male face 1.stl", "PolygonObjects"];
We convert to a 2D GraphicsComplex as seen from 40 different view angles:
imgrLargeHead[i_] := Delete[First[
ImageGraphics[
Image[
Graphics3D[{FaceForm[LightOrange], EdgeForm[], largeHeadPolys},
Boxed -> False,
ViewVector -> 100 {Cos[i Pi/20], Sin[i Pi/20], 0.05}]],
9] /. {x_?(And[NumericQ[#], Not[IntegerQ[#]]] &),
y_} :> {x - 545, y - 50}/350], {2, 1}]
largeHeadVideo =
FrameListVideo[
ParallelTable[
Image@Graphics[imgrLargeHead[i],
PlotRange -> {{-1.5, 1.5}, {-.2, 3}}], {i, 0, 39}]];

The GraphicsComplex can be easily converted to its anamorphic map in the x-y plane using the function cylAnamorphMapCF.
No need to apply the function to all 34, 496*3 or 103, 455 vertices but only to the visible 3, 374 coordinates of the lines and Bezier curves created by ImageGraphics! By running the view angle over the full circle, we can create 40 frames to make an anamorphic video:

Putting an appropriate cylindrical mirror on the iPad converts the anamorphic images into realistic ones and restores the original 3D video:

I hope this was useful. Now you can try yourself to create realistic 3D videos from hardly recognizable 2D images. Have fun!
 Attachments:
Attachments: