Hey Peter! Thanks for your interest. We're still actively working on the proof (and now a few others including this one from nks). It turns out after some decently involved combinatorics that the Hat tile is actually a combinatorial hexagon, as is its cluster super tile. Consequently, in addition to the already-awesome HatTrialityTree, we also have HatHexagons. This is fully a new way to build the hat tiling, except that it leaves holes where the reflected tiles are:
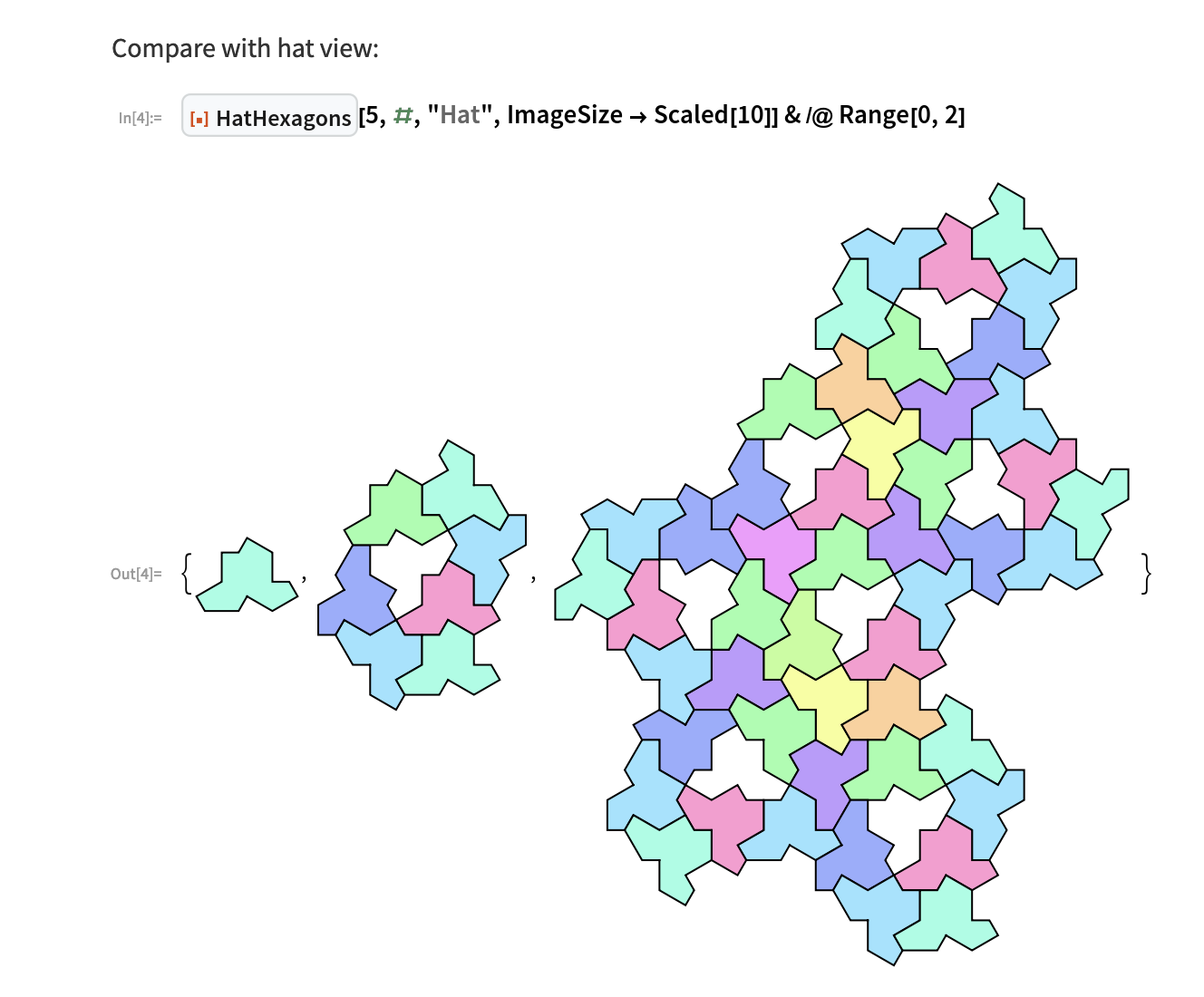
Of course, once you realize (and prove!) that the Hat is actually a hexagon, then it becomes possible to build hat tilings using the SAT solver. That's what we're currently working on for the last phase of the proof. "Oz is ever 浮", to adapt a lyric to the situation.
In the meantime, MoMath is having a contest for Hat-related creations, so if you have anything to contribute, perhaps send it to NYC and see what they say? Even if you don't already have something, you could probably get something quickly using the WFR's... Anyways, have fun and keep puzzling!