Many years ago I (and Tom Sibley) proved that any tiling (finite or infinite) with Penrose rhombs is 3-colorable as a map (a question raised by John Conway). And later the same was proved for Kites and Darts. So I wonder if the same is true for hats. Ed: If you send me a pile of hats I can run my 3-coloring program on it. I even made a carpet showing 3-colored rhombs.

I didn't get a good svg from the app website, I think: ResourceFunction::usermessage : SVGImport::format: "/Users/pbarendse/Downloads/output(2).svg" does not appear to be a valid SVG file. >>

Can the single tile be generated by some kind of morphing of Penrose's kite and dart?

You could try mapping the "drafter" Triangle into Penrose triangles and hope that the angles / matching rules work out. But I would guess no because how difficult (impossible?) it would be for patterns fitting on a hexagonal grid to ever allow five-fold centers of symmetry.

As far as structural analysis is concerned, Figure 2.12 could be a good place to start. It looks a bit like this space filling tree dragon we discovered at winter school:

In the future we'll probably get a definition of the tree structure itself, separate from definition in tiling context, but who will be the first to find it?

Hey Peter! Thanks for your interest. We're still actively working on the proof (and now a few others including this one from nks). It turns out after some decently involved combinatorics that the Hat tile is actually a combinatorial hexagon, as is its cluster super tile. Consequently, in addition to the already-awesome HatTrialityTree, we also have HatHexagons. This is fully a new way to build the hat tiling, except that it leaves holes where the reflected tiles are:

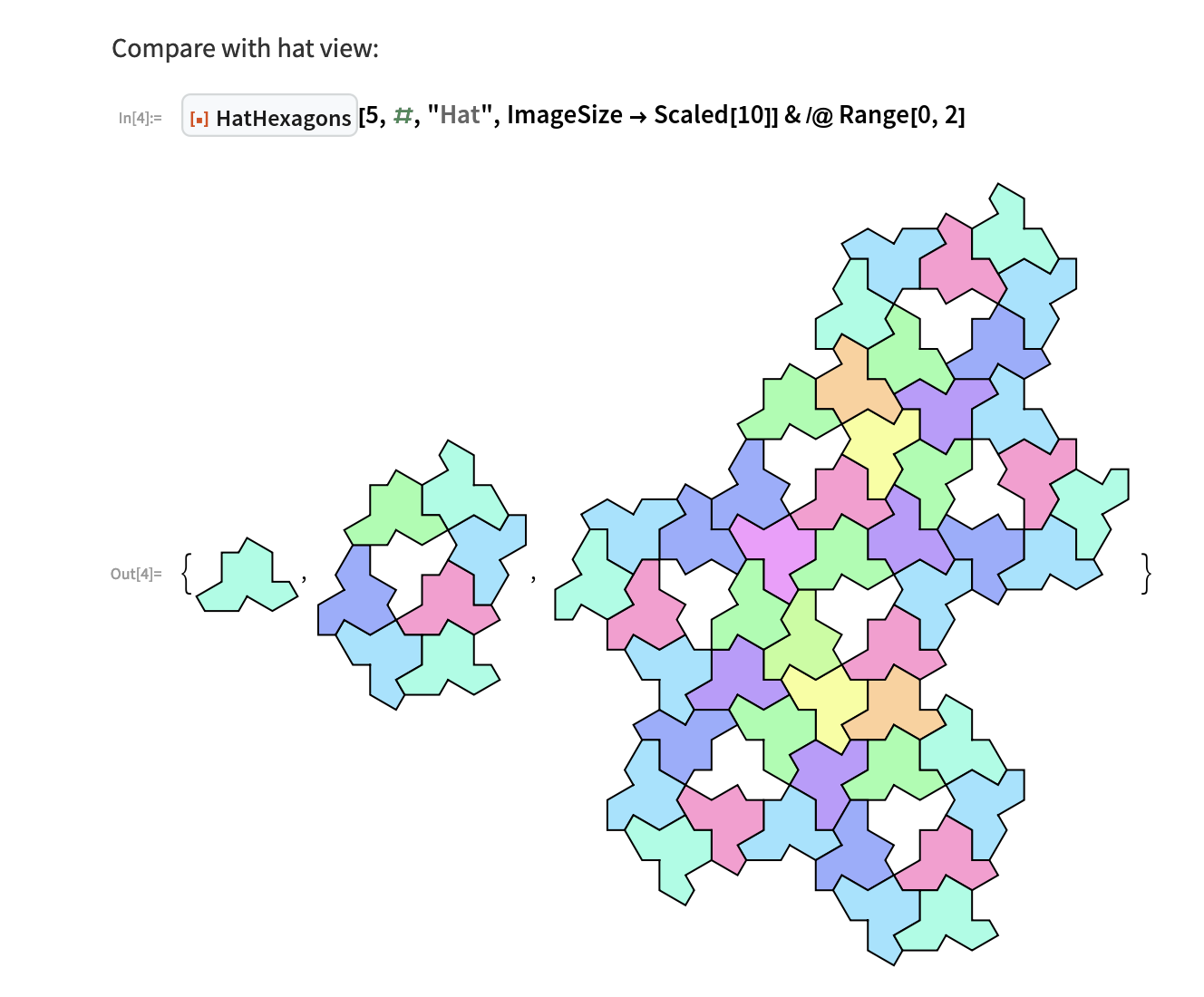
Of course, once you realize (and prove!) that the Hat is actually a hexagon, then it becomes possible to build hat tilings using the SAT solver. That's what we're currently working on for the last phase of the proof. "Oz is ever 浮", to adapt a lyric to the situation.

In the meantime, MoMath is having a contest for Hat-related creations, so if you have anything to contribute, perhaps send it to NYC and see what they say? Even if you don't already have something, you could probably get something quickly using the WFR's... Anyways, have fun and keep puzzling!