High-order series solution of the ODE around x=0 followed by a Pade approximation. difference calculates the difference of the approximation to the right boundary value. It also returns the actual Pade approximation.
difference[\[Alpha]In_Real,\[Xi]_,{prec_, pdO_}] :=
Module[{\[Alpha]=SetPrecision[\[Alpha]In, prec],diff,sol,series,pd,u,x,\[Delta]},
series=\[Alpha] x -\[Alpha]/8 x^3 ;
Do[diff=u''[x]+u'[x]/x-u[x]/x^2+u[x]-u[x]^3 /.
u->(Function@@{x,series+C x^M+O[x]^(M+1)});
series=series + Together[C x^M /. First[Solve[diff[[3,1]]==0,C]]],{M,5,2pdO+5,2}];
pd=PadeApproximant[series,{x,0,{pdO,pdO}}];
stepData={\[Alpha],\[Delta]=Tanh[10/Sqrt[2]] - pd/. x->10};
{\[Delta], pd /. x -> \[Xi]}
]
Example
difference[0.58318 , x, {20, 20}]
{0.2435578857088556, (0.58318000000000003 x +
0.27407625855333046 x^3 + 0.051256728918896911 x^5 +
0.0048322482238297771 x^7 + 0.00023632082879286407 x^9 +
5.1729410403285544*10^-6 x^11 + 8.2185843137751949*10^-9 x^13 -
1.06931812684189022*10^-9 x^15 - 2.2863733027673254*10^-12 x^17 +
7.6295697669084428*10^-14 x^19)/(1 + 0.59496854925294154 x^2 +
0.142883728435766338 x^4 + 0.0176772849277092897 x^6 +
0.00118228825938525016 x^8 + 0.000039832791262778028 x^10 +
4.5345802881727914*10^-7 x^12 - 5.5226863238549098*10^-9 x^14 -
9.7254616067217217*10^-11 x^16 + 6.0544145050658359*10^-13 x^18 +
3.9887426264821583*10^-15 x^20)}
Find slope at x=0 to any desired precision (by increasing prec and pdO). Say 15 digits.
Monitor[
fr = FindRoot[
difference[\[Alpha], x, {100, 200}][[1]], {\[Alpha], 0.5831, 0.5832}, WorkingPrecision -> 60, PrecisionGoal -> 16,
Method -> "Brent", Evaluated -> False];,
stepData]
fr
{\[Alpha] -> 0.583189634418924769412413009673771234659851269345508491782915}
The rational approximate solution.
uSol = difference[\[Alpha] /. fr, x, {100, 200}][[2]];
Plot[Evaluate[uSol], {x, 0, 10}, PlotRange -> All]
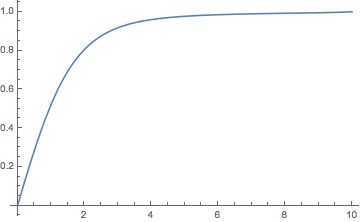
Check right boundary condition
(uSol /. x -> 10) - Tanh[10/Sqrt[2]]
-2.6496232607434627305318392508171048229727621206337120044345649125837*10^-27
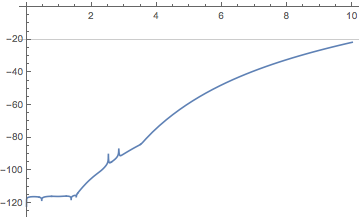
Check ODE. It is fulfilled to 20 digits everywhere.
odeDiff = u''[x] + u'[x]/x - u[x]/x^2 + u[x] - u[x]^3 /. u -> Function[x, Evaluate[uSol]];
Quiet[ Plot[Log10[Abs[odeDiff]], {x, 0, 10}, WorkingPrecision -> 200,
GridLines -> {None, {-20}}, PlotRange -> {Full, {All, 0}}], Plot::precw]
Notebook is attached.
 Attachments:
Attachments: