Hi,

It is by the way indeed interesting to use graphs to visualise this:

Graph[# -> Total[IntegerDigits[#]^2] & /@ Range[10000]]

It turns out that there is a skeleton that is relatively stable.

GraphPlot[# -> Total[IntegerDigits[#]^2] & /@ Range[1000], Method -> "CircularEmbedding"]

and this

GraphPlot[# -> Total[IntegerDigits[#]^2] & /@ Range[200], Method -> "LinearEmbedding"]

look pretty, too, and have a meaning. I think, however, that the Layered Graph is the best visualisation:

LayeredGraphPlot[# -> Total[IntegerDigits[#]^2] & /@ Range[200]]

The upper graph contains the sad numbers and the lower one the happy ones. This also explains why you always reach one out of nine numbers. The lower graph has a fixed point. You always get to "1" and then stay there - that's happy. If you carefully look at the other graph you see that there is a cycle of eight vertices.

If you want to see that cycle you can use:

g = Graph[# -> Total[IntegerDigits[#]^2] & /@ Range[1000]];
cycle=FindCycle[g]
(*{{4 -> 16, 16 -> 37, 37-> 58, 58-> 89, 89-> 145, 145 -> 42, 42-> 20, 20-> 4}}*)

This can be used to highlight the subgraph:

HighlightGraph[g, cycle]

If you compare that to the table of my first reply all numbers are accounted for.

Cheers,

Marco

Hi there,

this is actually quite nice. Here is a function that generates the lists.

f[start_] := Module[{list = {start}}, NestWhileList[Total[IntegerDigits[#]^2] &, start, Unequal, All]]

We can now generate that for the first, say 100 integers:

Table[f[k][[-1]], {k, 1, 100}]

The ones indicate happy numbers - all the others are sad. The interesting bit is that the sequences only reach one out of nine numbers:

Histogram[Table[f[k][[-1]], {k, 1, 100000}], 200]

or

Tally[Table[f[k][[-1]], {k, 1, 100000}]] //TableForm

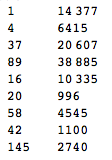
This table show the approximate relative frequencies of the terminal numbers.

This here reveals little of a pattern:

Partition[Table[f[k][[-1]], {k, 1, 1600}] /. {x_ /; x != 1 -> 0}, 40] // ArrayPlot

You can also play with this:

Manipulate[Partition[Table[f[k][[-1]], {k, 1, 1600}] /. {x_ /; x != 1 -> 0}, UpTo[j]] // ArrayPlot, {j, 5, 80, 1}]

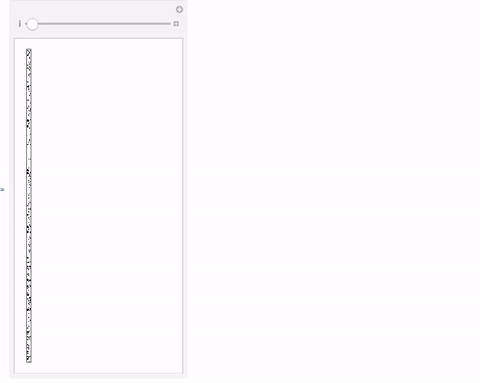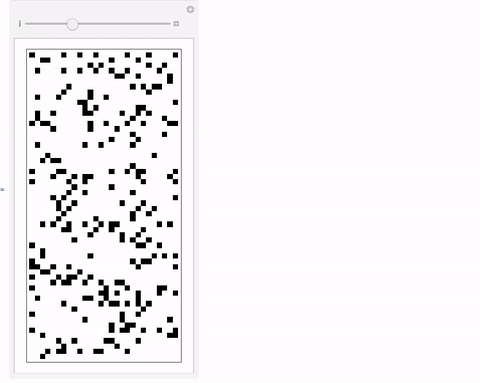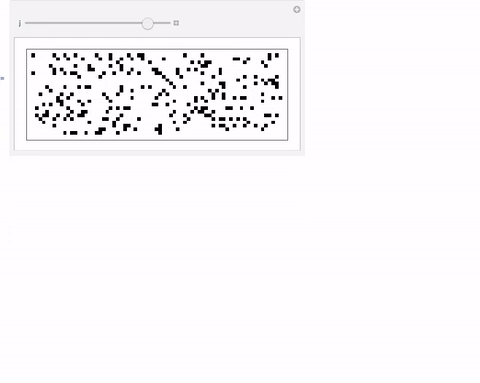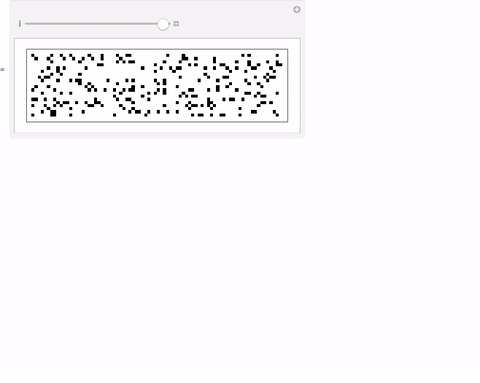
Cheers,

Marco

Also interesting the sequence in other bases:

ClearAll[gfun]
gfun[n_,b_:10]:=(#<->Total[IntegerDigits[#,b]^2])&/@Range[n]
Dynamic[b]
out=Table[{b,Length[ConnectedComponents[gfun[10^5,b]]]},{b,2,30}];
ListPlot[out]

The number of components as a function of the base:

Hi Vitaliy,

this is a beautiful representation. I do think that it would be important to use directed edges. Also, this looks really nice if you look at all paths to either the fixed point or up the the first repetition. If you plot that with overplayed (partially transparent) edges - similar to this beautiful post by @Bernat Espigulé Pons, you will see that a certain network gets more and more dominant. The outermost leaves/fringes get more and more "bushy". The tree grows, but there are some main arteries that lead to the fixed point or the cycle.

The frequencies in my first table obviously relate to the "trees" attached to the fixed point and the elements of the cycle respectively.

Cheers, Marco

PS: Still preparing the presentation for the Digital Humanities Conference at Oxford. Looking forward to meeting you there!

Maybe not a constant but it does appear to be approaching a simple function as it approaches infinity, maybe linear or maybe a logarithmic.

A spectral image of the FFT of this series may be interesting.

Hi Marco

Thank you very much for putting so much effort into this. You have shown me many ways to play around with these numbers and I find them very interesting. I'm looking forward to experimenting with all the input you gave me.

Have a good one!