Dear All,

that is indeed interesting. I also believe that the exact distribution is unknown but it can be approximated by a GammaDistribution, see:

https://arxiv.org/pdf/1207.0608.pdf

https://arxiv.org/pdf/1612.02375.pdf

https://www.sciencedirect.com/science/article/pii/002608008990030X

http://www.scipress.org/journals/forma/pdf/1804/18040221.pdf

http://www.eurecom.fr/~arvanita/PVT.pdf

Interestingly, if you run the code in @Vitaliy Kaurov's cod for 50000 points you obtain:

dis = FindDistribution[areas]
(*GammaDistribution[3.2718, 0.0000197063]*)

I managed to get it done for 500000 points. I think that the edge effects should be getting smaller; as the area increases faster than the circumference.

So I obtain:

dis = FindDistribution[areas, 5]

(*
{MixtureDistribution[{0.658342, 0.341658}, {MaxwellDistribution[2.92588*10^-6], GammaDistribution[7.1867, 1.37091*10^-6]}], 

ExtremeValueDistribution[4.80446*10^-6, 2.73831*10^-6], 

GammaDistribution[2.94963, 2.17794*10^-6], 

BetaDistribution[2.94962, 459143.], 

MixtureDistribution[{0.687855, 0.312145}, {MaxwellDistribution[2.82857*10^-6], 
   LogNormalDistribution[-11.5031, 0.28619]}]}*)

This happens when we plot all of them:

Plot[Evaluate[PDF[#, x] & /@ dis], {x, 0, 0.00003}, PlotRange -> All, LabelStyle -> Directive[Bold, 16]]

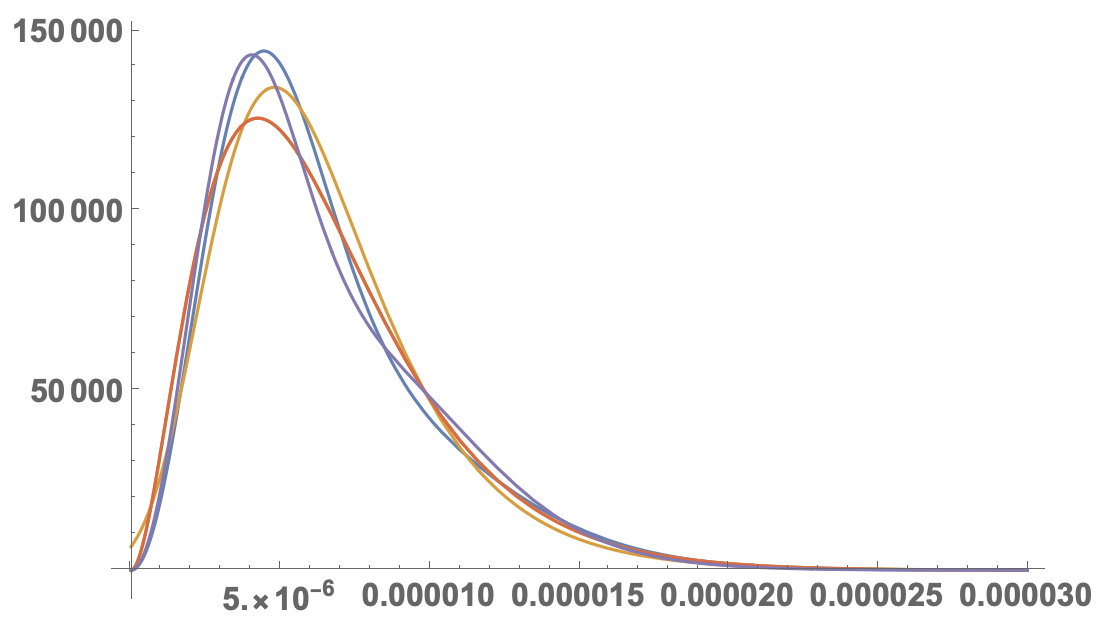
If you compare that with the histogram:

Show[Histogram[areas, 200, "PDF"], Plot[Evaluate[PDF[#, x] & /@ dis], {x, 0, 0.00003}, PlotRange -> All,LabelStyle -> Directive[Bold, 16]]]

I would say that the second (ExtremeValueDistribution) fits best:

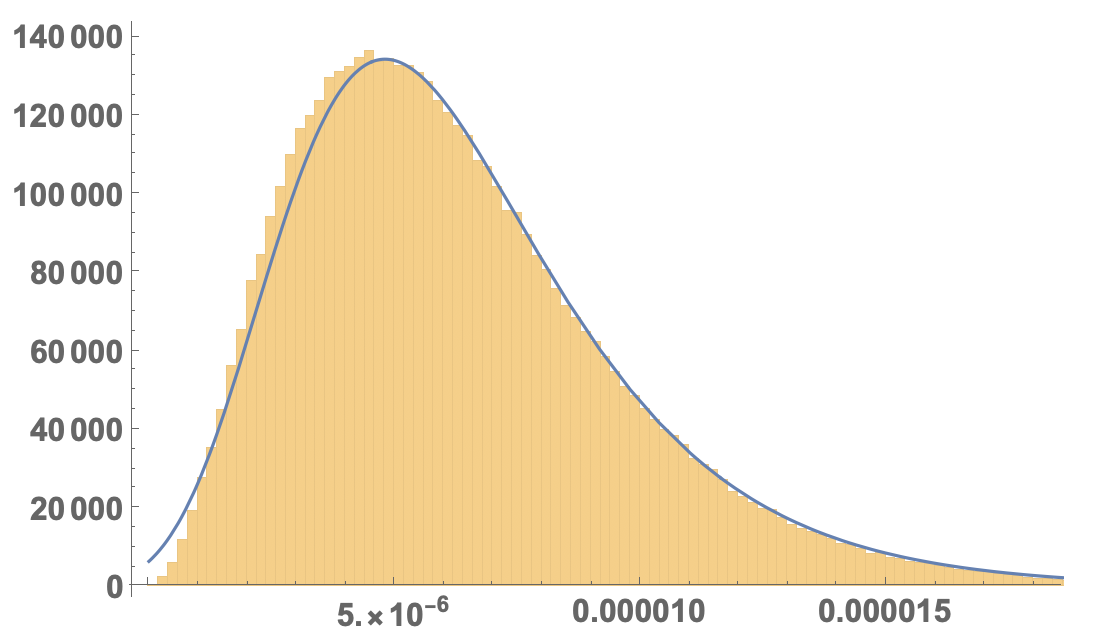
but it does not get the small areas quite right.

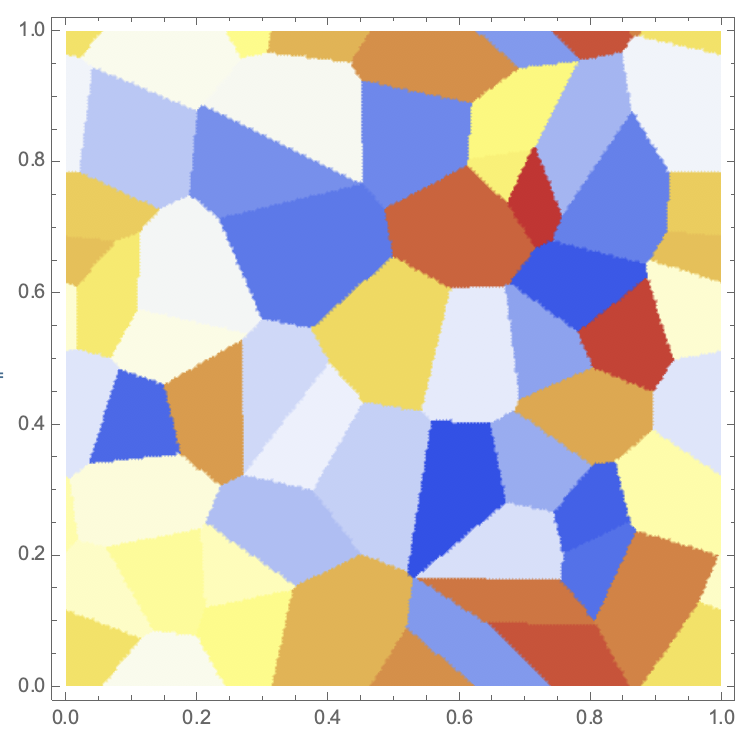
Regarding the boundary effects, one might also (similar to what Sander suggests) use the torus as the geometry:

disfun[x_, y_] := Sqrt[Min[Abs[x[[1]] - y[[1]]], 1 - Abs[x[[1]] - y[[1]]]]^2 + Min[Abs[x[[2]] - y[[2]]], 1 - Abs[x[[2]] - y[[2]]]]^2]

M = 50; nf = Nearest[Rule @@@ Transpose[{RandomReal[1, {M, 2}], Range[M]}], DistanceFunction -> disfun]

DensityPlot[First[nf[{x, y}]], {x, 0, 1}, {y, 0, 1}, PlotPoints -> 100, ColorFunction -> "TemperatureMap"]

Cheers,

Marco

Very nice. Thanks for sharing. Some years ago I did this with 10^9 cells. If I recall correctly the left side is a bit higher (more probably) than a gamma distribution.

To remove any edge-effects, what people do is: take random points in a square, and then copy the square 9 times in a 3*3 grid, such as to emulate period boundary conditions. Then take only the polygons which center is in the center unit square…

Great stuff!

–SH

I looked at different things: how many sides, angles, area, perimeter, and many conditionally averaged quantities. But area of the PDF as well. But no analytical shape is known for it. I believe that there is something known for perimeter.

I don't find it all that surprising that the result is a Gamma distribution. The 1-d case is well known as it is the distribution of interarrival times of a Poisson process and is exponentially distributed. The exponential distribution is a special case of the Gamma so maybe you're onto something.

Very Nice. I am aware that the distribution of Lightning strike intensity from a Thunderstorm also closely follows a Gamma Distribution. Could this be due to cells of charge inside the cloud which organise like a Voronoi topology? Does a Gamma distribution also arise from a 3 D distribution of volumes of a Vornoi tesellation?