Hi,
I guess that you can see the problem when you use the option Mesh-> All.
f[t_] := Piecewise[{{0, t <= 0}, {0.2 t^3,
0 < t <= 0.5}, {0.025 + 0.15*(-1 t + 2 t^2),
0.5 < t <= 2.5}, {3.15 - 0.6 (6.5 t - 3 t^2 + 1/3*t^3),
2.5 < t <= 3}, {-2.25 + 1.5 t,
3 < t <= 5}, {22.75 - 13.5 t + 3 t^2 - 0.2 t^3,
5 < t <= 5.5}, {-10.525 + 4.65 t - 0.3 t^2,
5.5 < t <= 7.5}, {-94.9 + 38.4 t - 4.8 t^2 + 0.2 t^3,
7.5 < t <= 8}, {7.5, True}}]
and
Plot[f[t], {t, 0, 8}, Mesh -> All]
gives
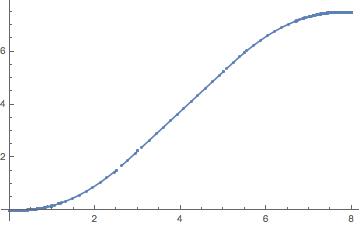
You can plot more points and the problem is remedied:
Plot[f[t], {t, 0, 8}, PlotPoints -> 200]
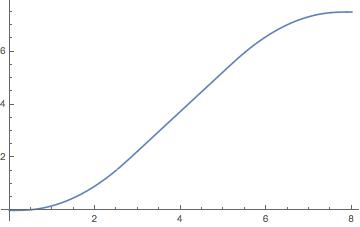
Here is the implementation with Which that indeed does not cause any trouble in the first place:
g[t_] := Which[t <= 0, 0, 0 < t <= 0.5, 0.2 t^3, 0.5 < t <= 2.5,
0.025 + 0.15*(-1 t + 2 t^2), 2.5 < t <= 3,
3.15 - 0.6 (6.5 t - 3 t^2 + 1/3*t^3), 3 < t <= 5, -2.25 + 1.5 t,
5 < t <= 5.5, 22.75 - 13.5 t + 3 t^2 - 0.2 t^3,
5.5 < t <= 7.5, -10.525 + 4.65 t - 0.3 t^2,
7.5 < t <= 8, -94.9 + 38.4 t - 4.8 t^2 + 0.2 t^3, True, 7.5]
Cheers,
M.