I realize that I am possibly the only Mathematica user to suffer from existential angst for the product, but still, its worth pausing to ask the question, what is Mathematica for? Meaning, what is its purpose?
But for those of you pragmatists tempted to roll your eyes and just get on with using it, let me motivate the question with a chart:
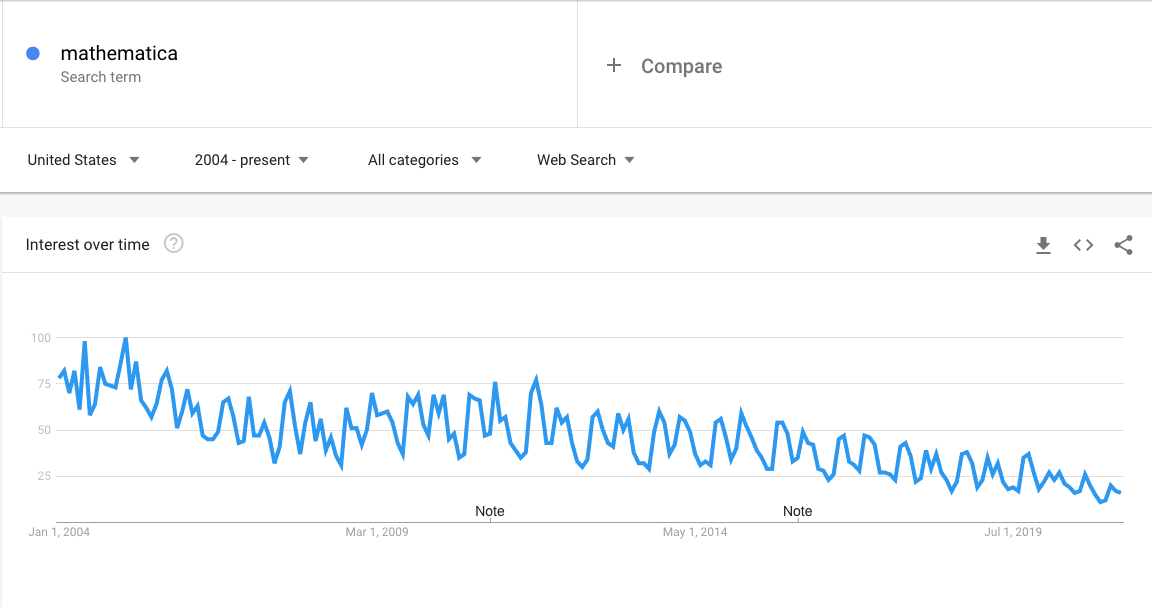
You don't need a model to figure out the long term trend in that time series. And someone, somewhere, in WR needs to be asking the question I am posing in this post, if they are seriously hoping to check that trend and reverse it.
Now, let's be fair here. Firstly this is not just a Mathematica issue. For example, here's the comparable chart for Matlab:
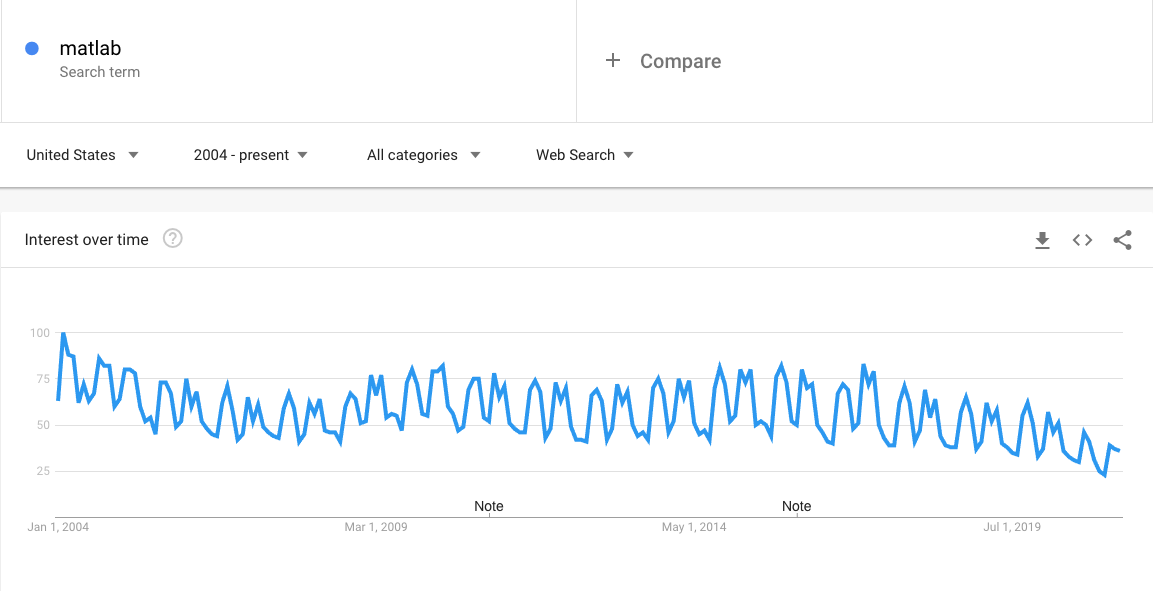
So I am not "picking on" Mathematica. Its a general problem for mathematical programming languages. Or perhaps I should say, more accurately, its a challenge for proprietary mathematical programming languages: 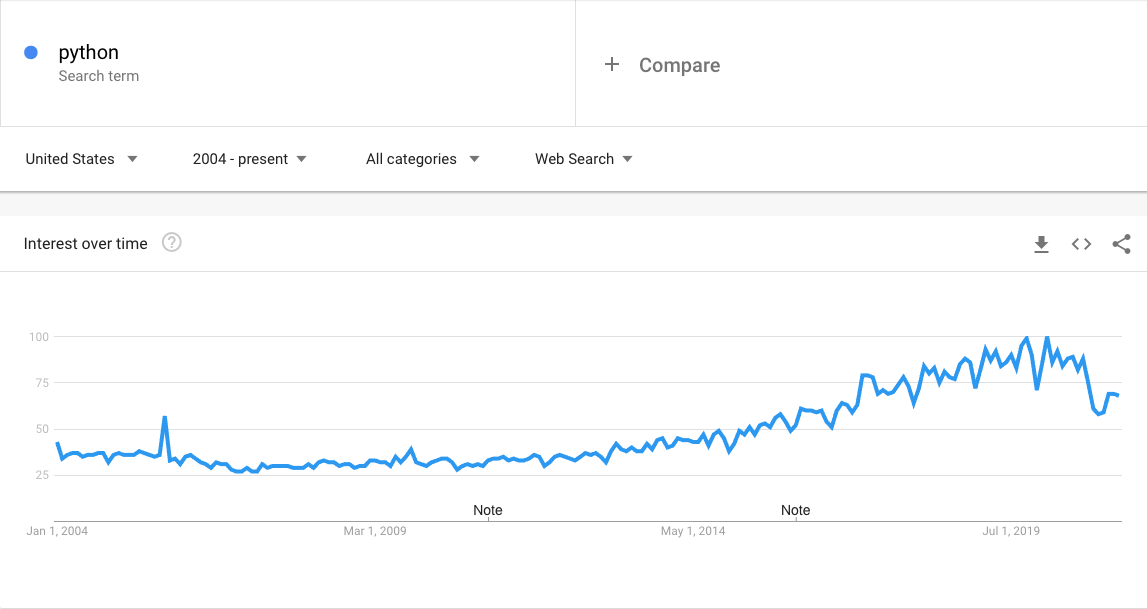
Now this "analysis" is of course over-simplistic. It could be, for example, that the downward trend in Mathematica interest is a reflection of a decision by WR to increase prices over time, to maximize profits, i.e. it could conceivably be a good thing. But I rather suspect otherwise and instead tend to believe that Mathematica is losing influence and relevance, regardless of whatever I may think of the product.
Another response might be: "Of course we are losing market share to license-free, direct competitor products. What's your point?". To which, I suppose, the answer might be: "Are you quite sure that is inevitable? Are there not examples of for-profit products that are so good they are able to maintain market share in the face of cost-free alternatives?".
The answer to that question is, of course, yes. But in order to maintain your competitive position you have to be crystal clear in your understanding of what the value proposition is, and why customers will (continue to) pay for your product. Which brings me to the subject of this post: what is Mathematica for? Because unless can answer that question, you can't answer the earlier one.
Now I have a theory that the generally held view in WR is that Mathematica is for any kind of programming task you can conceive of. It's a general purpose tool, limited in its capabilities only by your imagination. And at this point we could now queue up a 15 minute informercial featuring examples of applications from Astronomy to Zoology.
But just because you can do something in Mathematica doesn't mean you should: there are often better alternatives. Mathematica has developed into something like a Swiss Army knife, a general purpose tool you can use for almost any purpose. But, often times what you need is a tool with a specific purpose, like a screwdriver, which will make it much easier to complete the task you have in mind.
Let's take a simple example: spreadsheets. I have seen several attempts to get Mathematica to do the kind of thing that Excel can do effortlessly. And the question I always end up asking myself is: "why on God's green earth would anyone in their right mind try to use Mathematica for a task like that?". What is trivial to accomplish in a few seconds or minutes in Excel, typically takes hours of jumping through hoops with Mathematica to achieve a result that is almost always inferior. It's like trying to navigate a freeway in a spaceship, rather than a motor car. Sure, you can do it, buy why??
Another no-no is trying to develop stand-alone software applications in Mathematica. It's extremely hard to do - typically much tougher then using a language designed for that purpose.
On the other hand, there are some things that Mathematica excels at, such as:
- Mathematics/symbolic logic/symbolic manipulation: superb. Best of breed.
- Graphics (including animation) ditto
- Documentation. Also superb. Now as good at Matlab, possibly even superior.
After that, you could pick a bunch of different application areas in which Mathematica is great. But best of breed? I dont know.
Let's take an area I know a little about: time series analysis. prior to 2010, Mathematica was truly awful at handling time series. Basically it didn't. Gradually, over subsequent releases, Mathematica has made enormous strides in this area to the point where it is truly magnificent. For which someone at WL deserves (and I hope has received), several promotions. But despite this, Mathematica is still not best of breed in this area. Why? Because, unaccountably, it is still missing several vital elements of functionality such as Granger causality/ Cointegration and its implementation of important functionality like the Kalman Filter is horribly unintuitive.
This shows two things: (i) it is possible for WR to make Mathematica outstanding in almost any area it chooses to. it's just a question of focus. And (ii) to become best of breed, you need to finish the job! By which I mean, provide something close to 99% of the functionality that a professional practitioner in that area would expect to have available. if it chose to, WR could accomplish that in the time series area in a single release, I would guess.
The problem, I am suggesting, is that in trying to make Mathematica a product that is "all things to all men", it fails to achieve the status of being indispensable to practitioners in a more limited subset of subject areas.
Ok let's go with this conjecture for a moment. Let's wave a magic wand and imagine that we can change Stephen Wolfram's vision about his flagship product, which he has sweated blood over for the last 20-30 years (in other words, this is never going to happen - but its still fun to play the game).
What core capabilities would you have WR focus on with the aim of making Mathematica an indispensable product in that area?
Here are my choices:
(i) Time series & econometrics. Mathematica is so close: just finish the job - it's a no-brainer!
(ii) Machine learning. This also means making sure that the GPU capability works as it should, first time and every time. Mathematica still has a way to go here and its a huge area. But I'm sure WR could do it.
(iii). Meta-Programming. This one is a BIG stretch. But it just happens that WL may have a huge potential competitive advantage, because the language is itself computational. in other words, the building blocks of the language can themselves be manipulated, which is exactly what you need for meta-programming. Try doing that in Python!
On this subject I would say that the starting point would be to create WL functionality capable of generating a single line of WL code that is sufficiently complex and interesting to win the Wolfram One-Liner competition. I realize that's a huge challenge and its not just about the difficulty of navigating the terrain of the Wolfram language. It also involves thinking about what "complex" and "interesting" mean, in this context.
Think of this as a Turing test, for Metaprogramming capability. Once it's passed, it would open up a floodgate of possibilities, both for WL aficionados but also, critically, for those who don't program in WL, or indeed in any language at all. For reference, check out whats going on in the world of "no -code" application environments.