I have looked at a number of example some similar to the ones above. Some word histories tell nice stories, for example about medicine. Here are three words for malaria:

Options[WordFrequencyPlot] = {"YearStart" -> 1800, "YearEnd" -> Now, 
   "Case" -> True, "Smooth" -> 3, "Scaling" -> None, 
   "Style" -> Automatic};

WordFrequencyPlot[words_, OptionsPattern[]] := 
 With[{$data = 
    WordFrequencyData[words, 
     "TimeSeries", {OptionValue["YearStart"], OptionValue["YearEnd"]},
      IgnoreCase -> OptionValue["Case"]]}, 
  DateListPlot[
   MapThread[
    Callout, {MeanFilter[#, 
        Quantity[OptionValue["Smooth"], "Years"]] & /@ Values[$data], 
     words}], ScalingFunctions -> OptionValue["Scaling"], 
   PlotRange -> All, PlotTheme -> "Detailed", 
   PlotStyle -> OptionValue["Style"], FrameTicks -> {Automatic, None},
    ImageSize -> Large, FrameLabel -> {"YEAR", "FREQUENCY in TEXT"}]]

WordFrequencyPlot[{"ague", "malaria", "paludism"}]

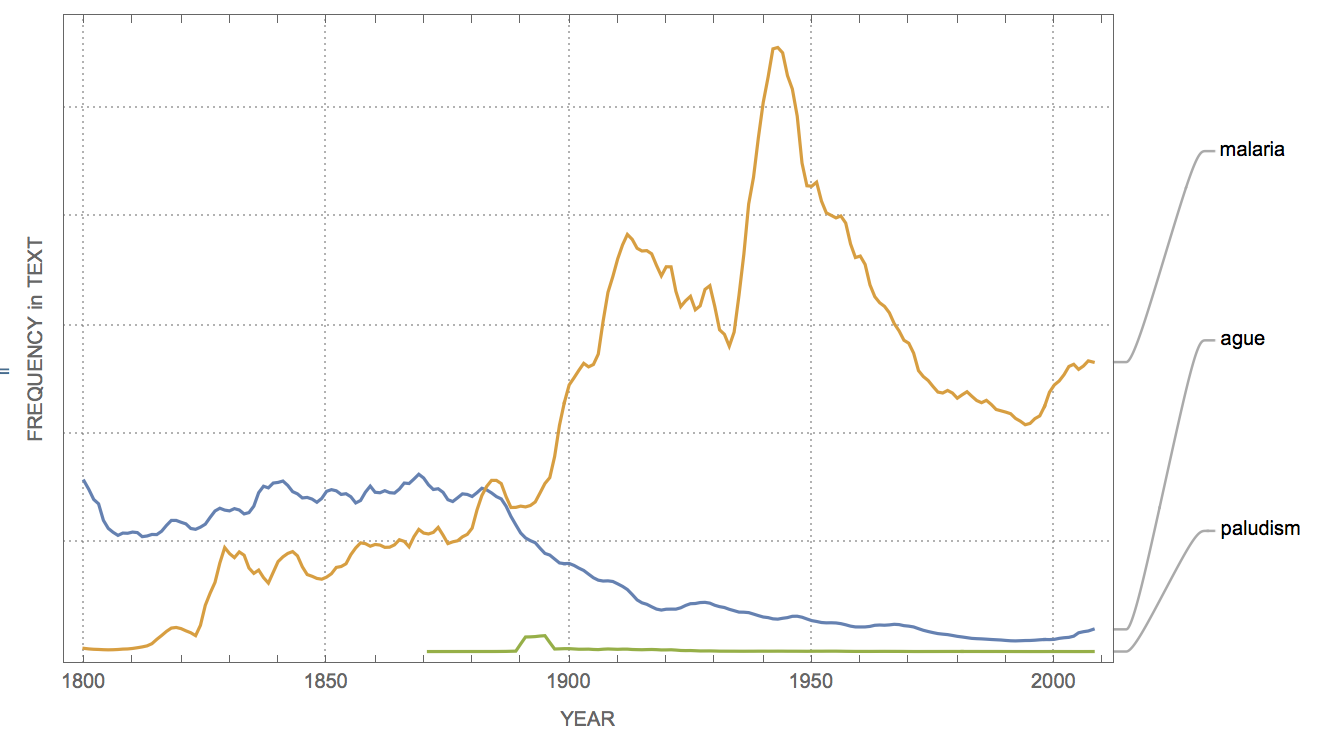
Until 1880, when Laveran first discovered the parasite, ague and malaria have basically the same frequency. Malaria is derived from malaria aria "bad air", whereas ague comes from acute febris "acute fever".

Sometimes we can also observe a shift in the frequency of words reflecting meaning the same thing

Options[WordFrequencyPlot] = {"YearStart" -> 1800, "YearEnd" -> Now, "Case" -> True, "Smooth" -> 3, "Scaling" -> None, "Style" -> Automatic};

WordFrequencyPlot[{"Moslem", "Muslim"}]

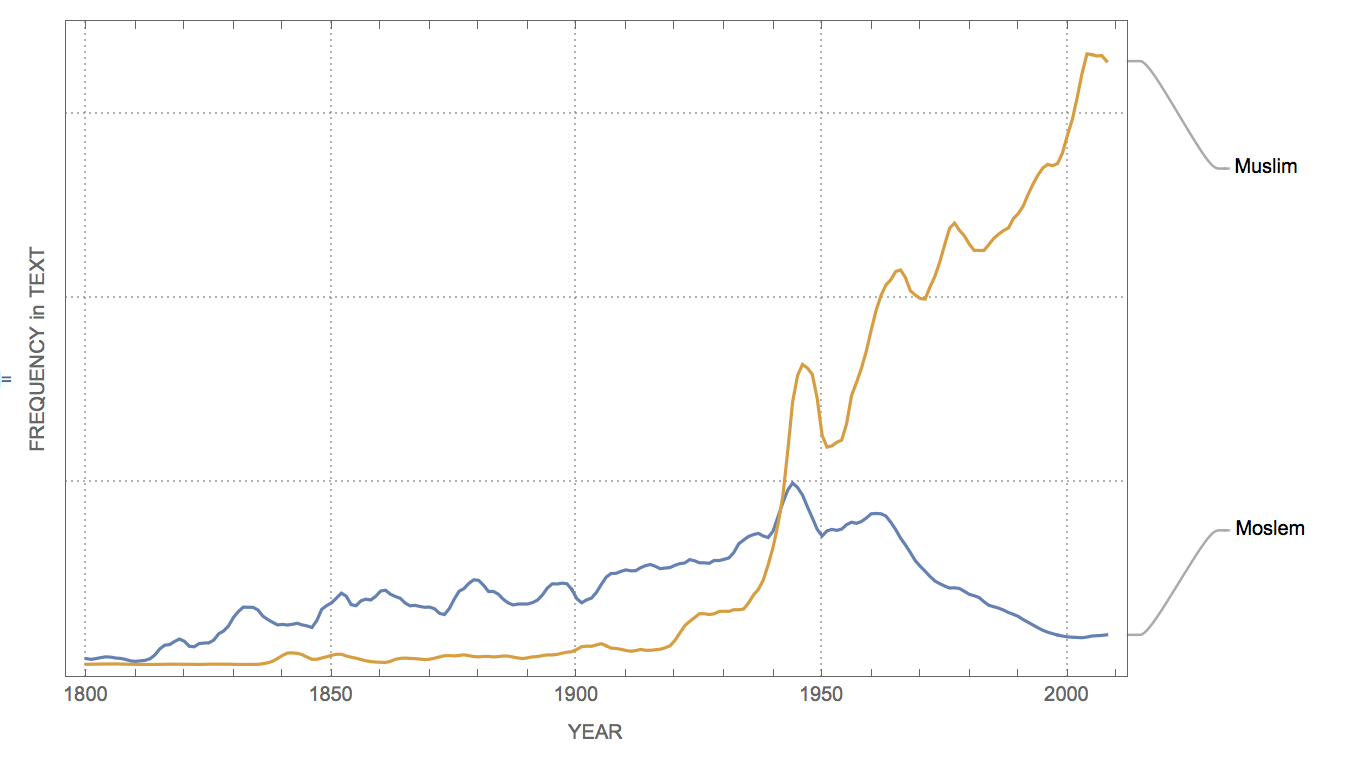
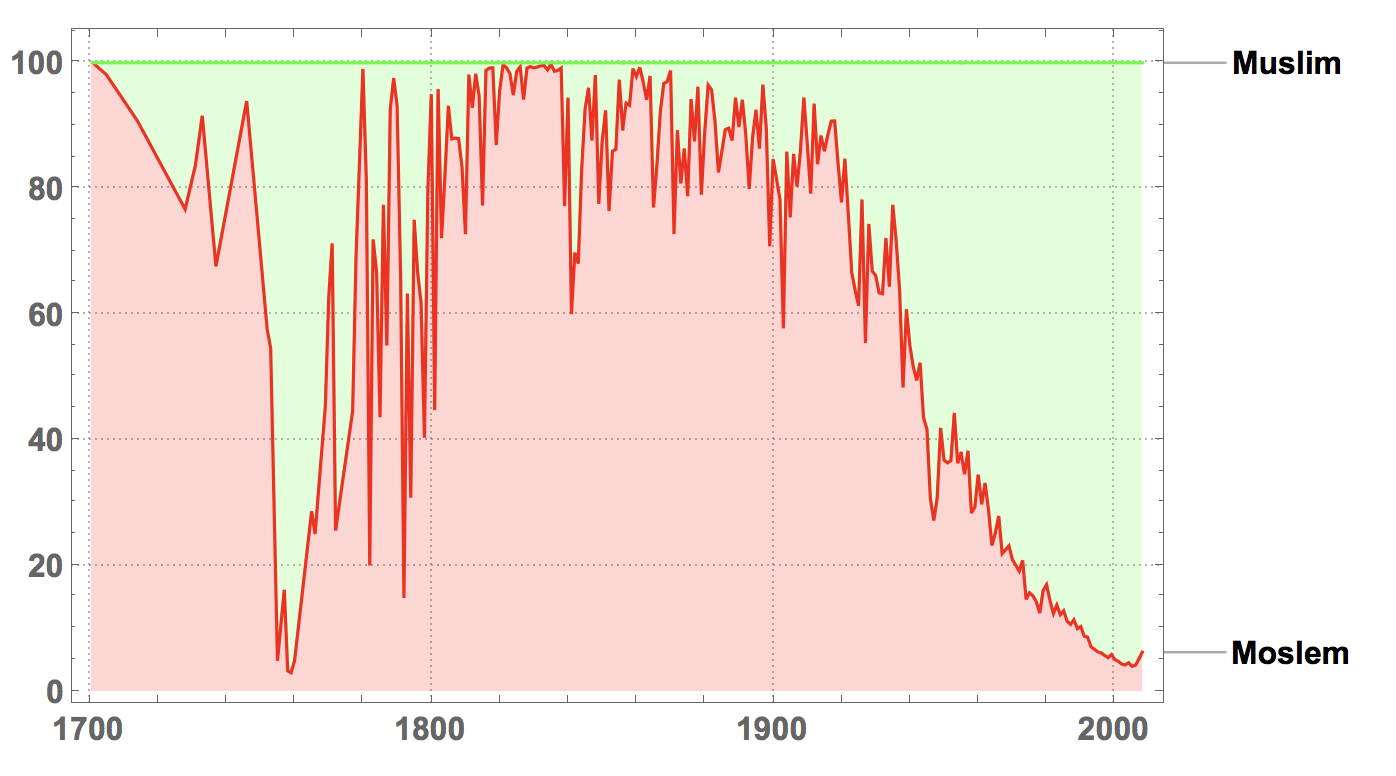
In those cases a relative frequency plot, i.e. displaying quantiles could be interesting:

StackedDateListPlot[
 MapThread[
  Callout, {Values[
    WordFrequencyData[{"Moslem", "Muslim"}, "TimeSeries"]], {"Moslem",
     "Muslim"}}], PlotRange -> All, PlotLayout -> "Percentile", 
 ImageSize -> Large, PlotStyle -> {Red, Green}, 
 LabelStyle -> Directive[Bold, 16], PlotTheme -> "Detailed"]

Such a plot is also useful to compare opposites like the words peace and war, which are also studied in an earlier post:

StackedDateListPlot[
 MapThread[
  Callout, {Values[
    WordFrequencyData[{"war", "peace"}, "TimeSeries"]], {"war", 
    "peace"}}], PlotRange -> All, PlotLayout -> "Percentile", 
 ImageSize -> Large, PlotStyle -> {Red, Green}, 
 LabelStyle -> Directive[Bold, 16], PlotTheme -> "Detailed"]

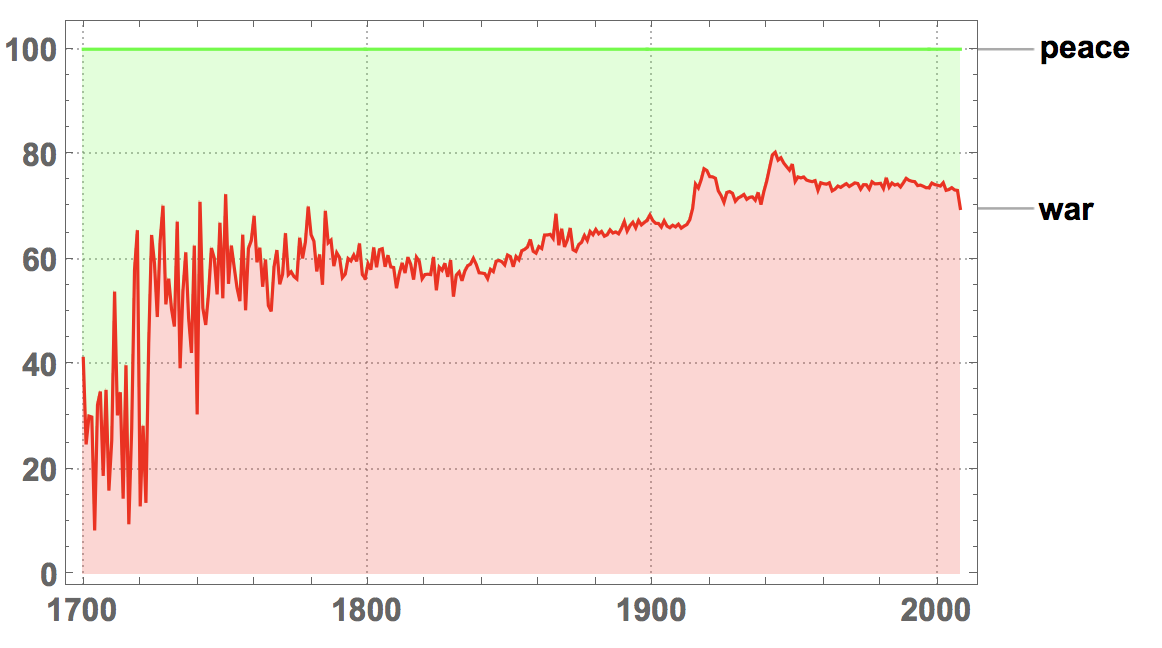
It is interesting to see that since about 1850 the word war is more frequent than peace.

These plot also reflect use of words such as bike and bicycle

StackedDateListPlot[
 MapThread[
  Callout, {Values[
    WordFrequencyData[{"bicycle", "bike"}, "TimeSeries"]], {"bicycle",
     "bike"}}], PlotRange -> All, PlotLayout -> "Percentile", 
 ImageSize -> Large, PlotStyle -> {Red, Green}, 
 LabelStyle -> Directive[Bold, 16], PlotTheme -> "Detailed"]

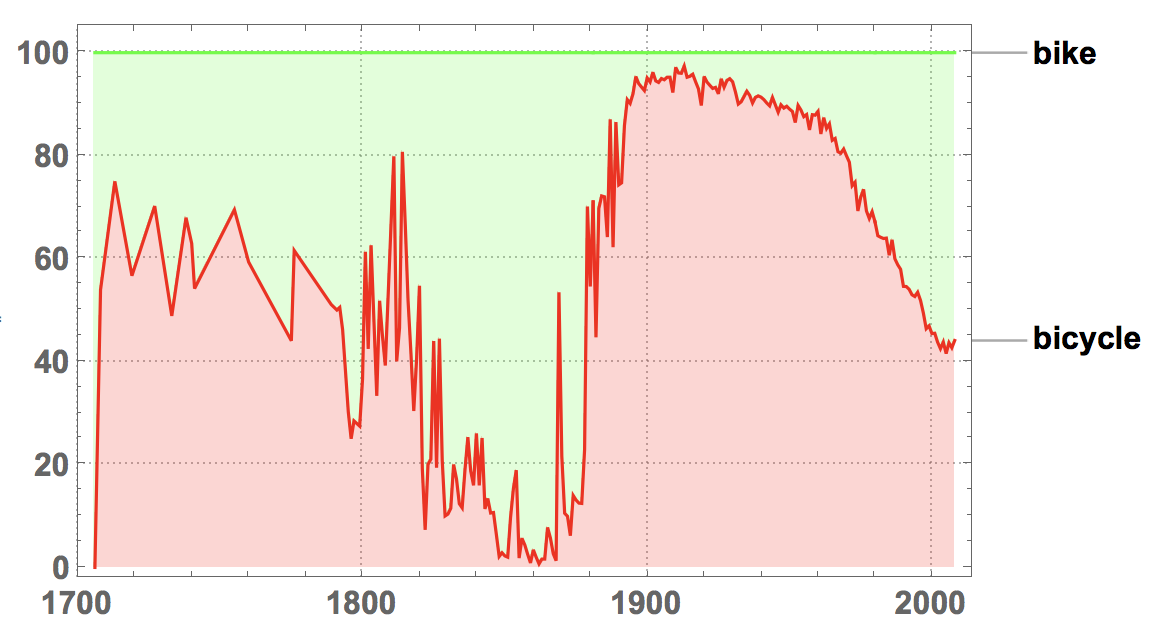
I would have expected that bike becomes more prominent during the 20th century. Between 1800 and 1880 is is also surprisingly common. I am not sure why, but this could be due to the other meaning of bike which is something like "nest or swarm of bees".

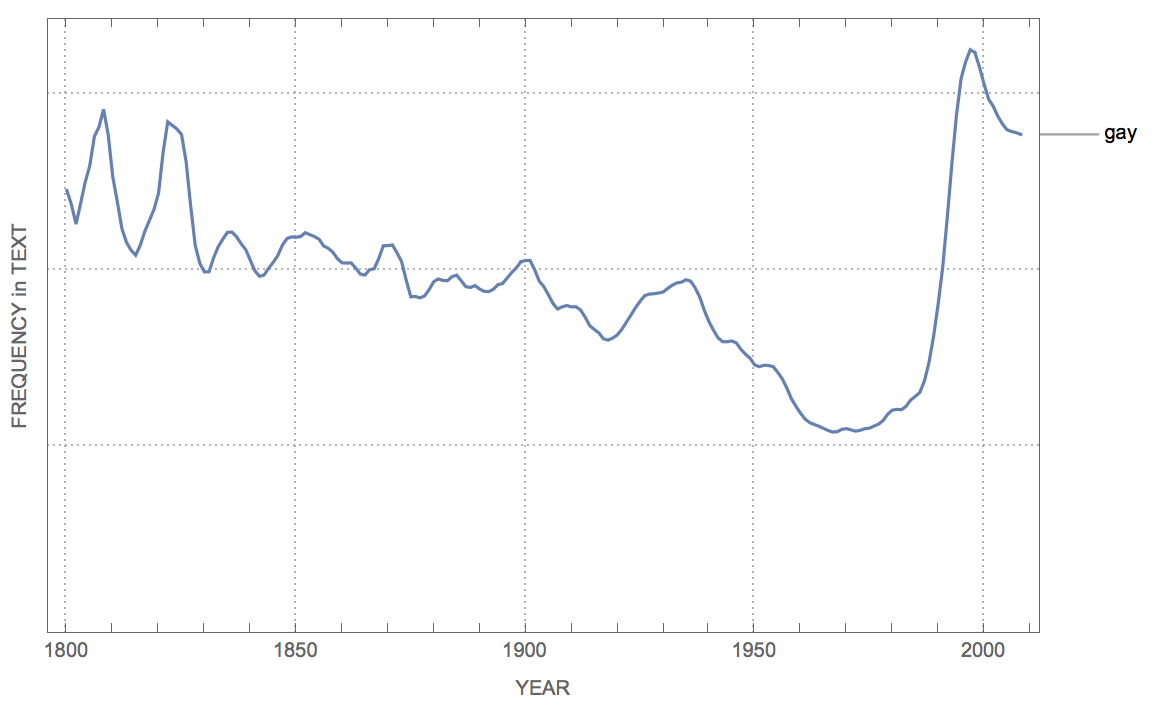
It would be interesting to consider the change of meaning of words. I tried to look at the word "gay" which has changed meaning over the years from lighthearted (13th century), bright and showy (14th century) and happy. It could also imply morality and mean gay women (prostitute) or gay man (womaniser), gay house (brothel). around 1900 it was something like "cheerful"; in the 1980 young users would use it to mean "lame, stupid" around 1990 it got to mean homosexual. I tried to use google n-grams to figure that out, but it didn't really work well. Here are words that are used close to gay over the years:

Table[{k, 
  StringSplit[
    StringSplit[
      StringSplit[
        StringSplit[
          URLExecute[
           "https://books.google.com/ngrams/graph?content=gay+*_ADJ&\
year_start=" <> ToString[k] <> "&year_end=" <> ToString[k + 20] <> 
            "&corpus=15&smoothing=3"], "direct_url="][[2]], 
        " width"][[1]], "gay%20"][[3 ;;]], "_"][[All, 1]]}, {k, 1800, 
  2000, 20}]

which gives

The frequency plot is:

Options[WordFrequencyPlot] = {"YearStart" -> 1800, "YearEnd" -> Now, 
   "Case" -> True, "Smooth" -> 3, "Scaling" -> None, 
   "Style" -> Automatic};

WordFrequencyPlot[{"gay"}]

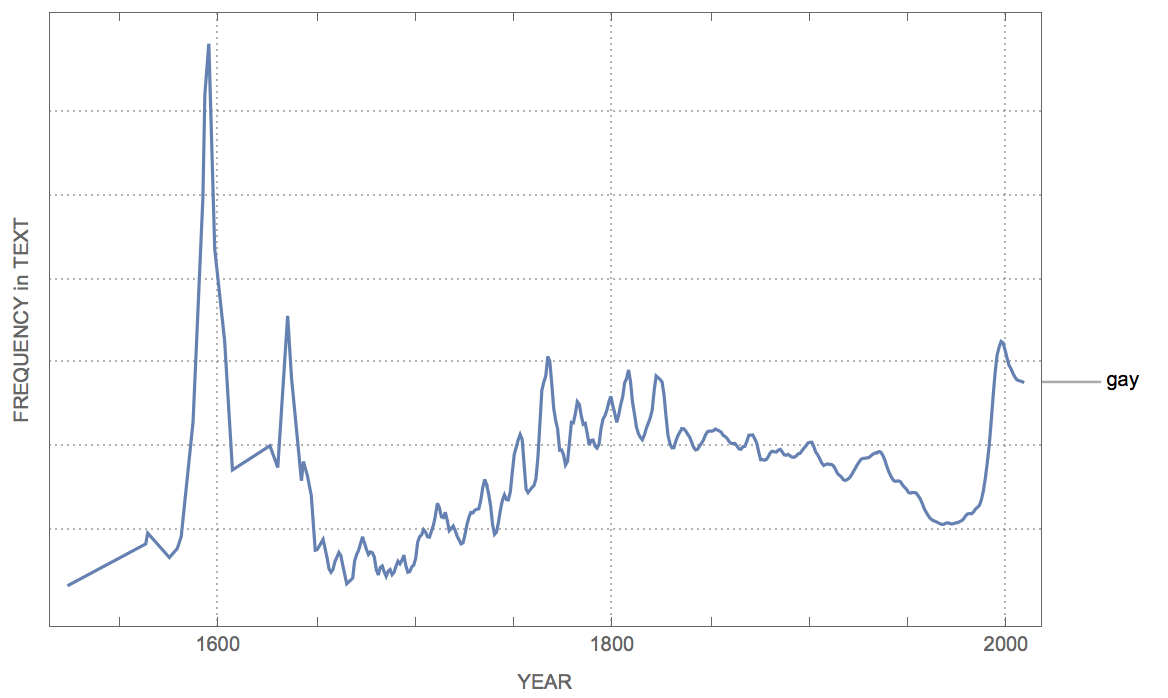
or over longer times:

Options[WordFrequencyPlot] = {"YearStart" -> 1500, "YearEnd" -> Now, 
   "Case" -> True, "Smooth" -> 3, "Scaling" -> None, 
   "Style" -> Automatic};

WordFrequencyPlot[{"gay"}]

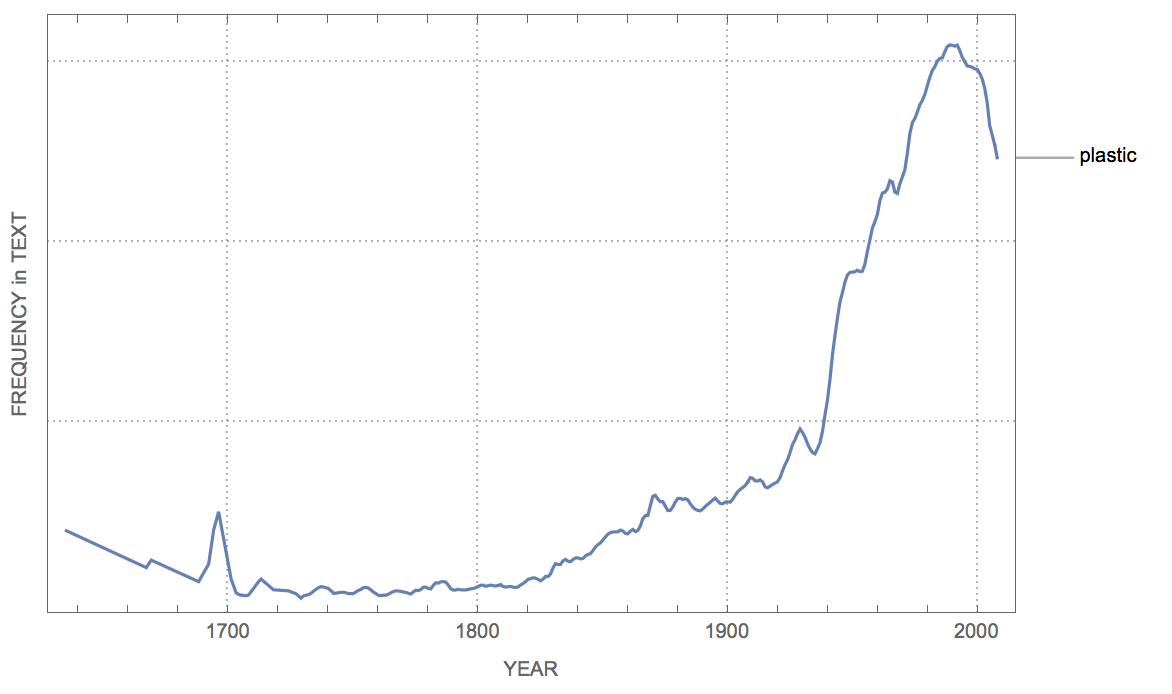
Also plastic has changed meaning from the the characteristic of being plastic to the material plastic:

WordFrequencyPlot[{"plastic"}]

In general we can see when different products have been developed:

WordFrequencyPlot[{"radio", "telephone", "computer", "car", "watch", 
  "electricity"}, "YearStart" -> 1700, "YearEnd" -> Now]

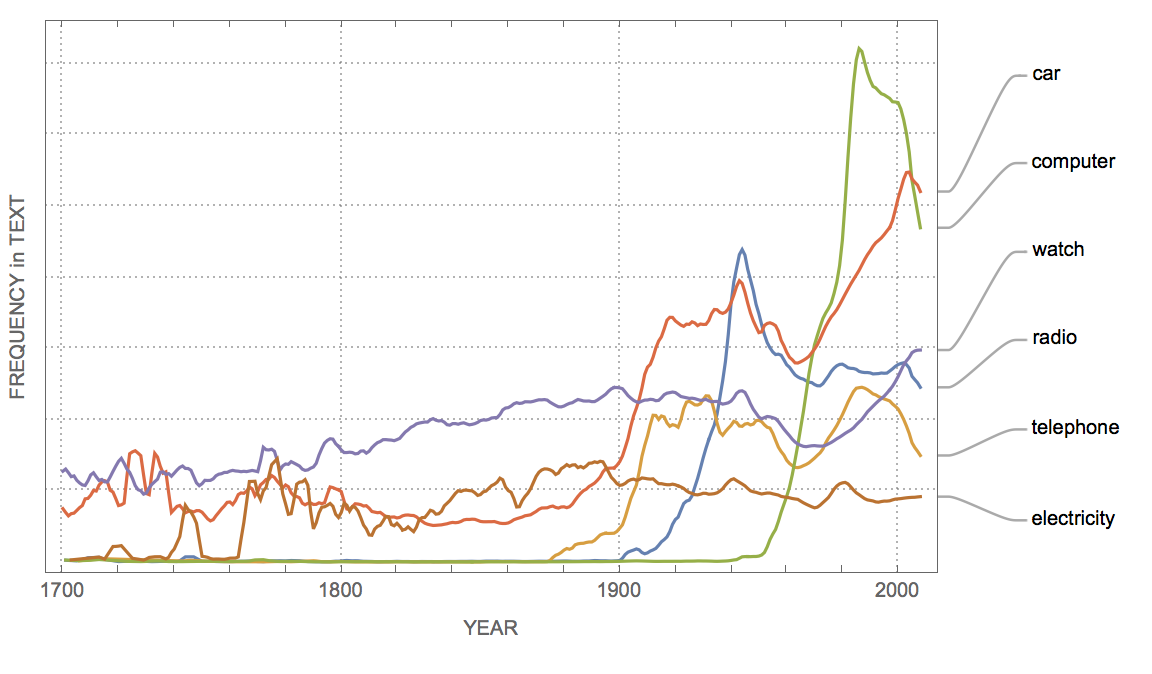
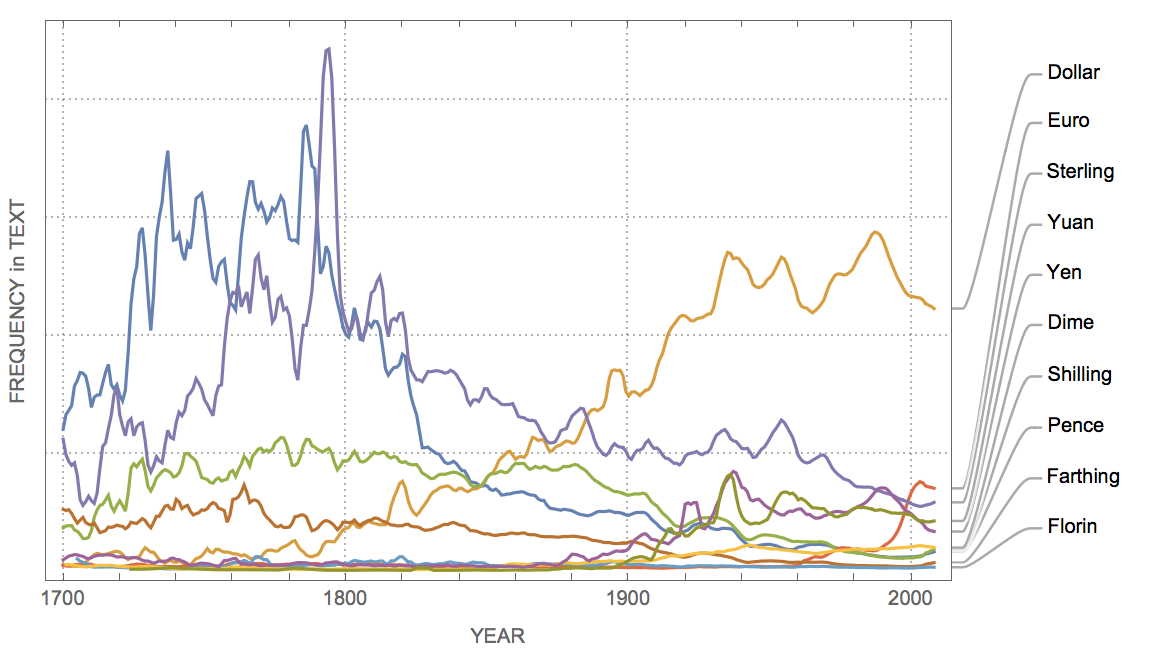
Of course, words can come out of fashion, too. For example:

WordFrequencyPlot[{"Pence", "Dollar", "Shilling", "Euro", "Sterling", 
  "Farthing", "Florin", "Dime", "Yen", "Yuan"}, "YearStart" -> 1700, 
 "YearEnd" -> Now]

In fact we can study this more systematically, by looking at the correlations between frequency curves:

words = {"war", "peace", "communism", "capitalism", "socialism", 
  "democracy", "unemployment", "conflict", "crisis", "terrorism", 
  "military", "welfare", "bomb", "weapons", "combat"}

worddata = (WordFrequencyData[#, "TimeSeries"])["Values"] & /@ words;

cm = Correlation[
   Transpose@
    worddata[[All, 
     1 ;; Min[
       Table[Length[worddata[[i, ;;]]], {i, 1, 
         Length[words] - 1}]]]]];

Column[{GraphicsRow[words[[1 ;;]], ImageSize -> 1000, Frame -> All], 
  Row[{GraphicsColumn[words[[1 ;;]], ImageSize -> 67, Frame -> All], 
    Overlay[{ArrayPlot[cm, 
       ColorFunction -> (ColorData["TemperatureMap"][(1 + #)/2] &), 
       Frame -> None, Mesh -> True, PlotRangePadding -> 0, 
       ImageSize -> 1000, ColorFunctionScaling -> False], 
      GraphicsGrid[Map[NumberForm[#, 2] &, cm, {2}], 
       ImageSize -> 1000]}]}]}, Alignment -> Right, Spacings -> 0]

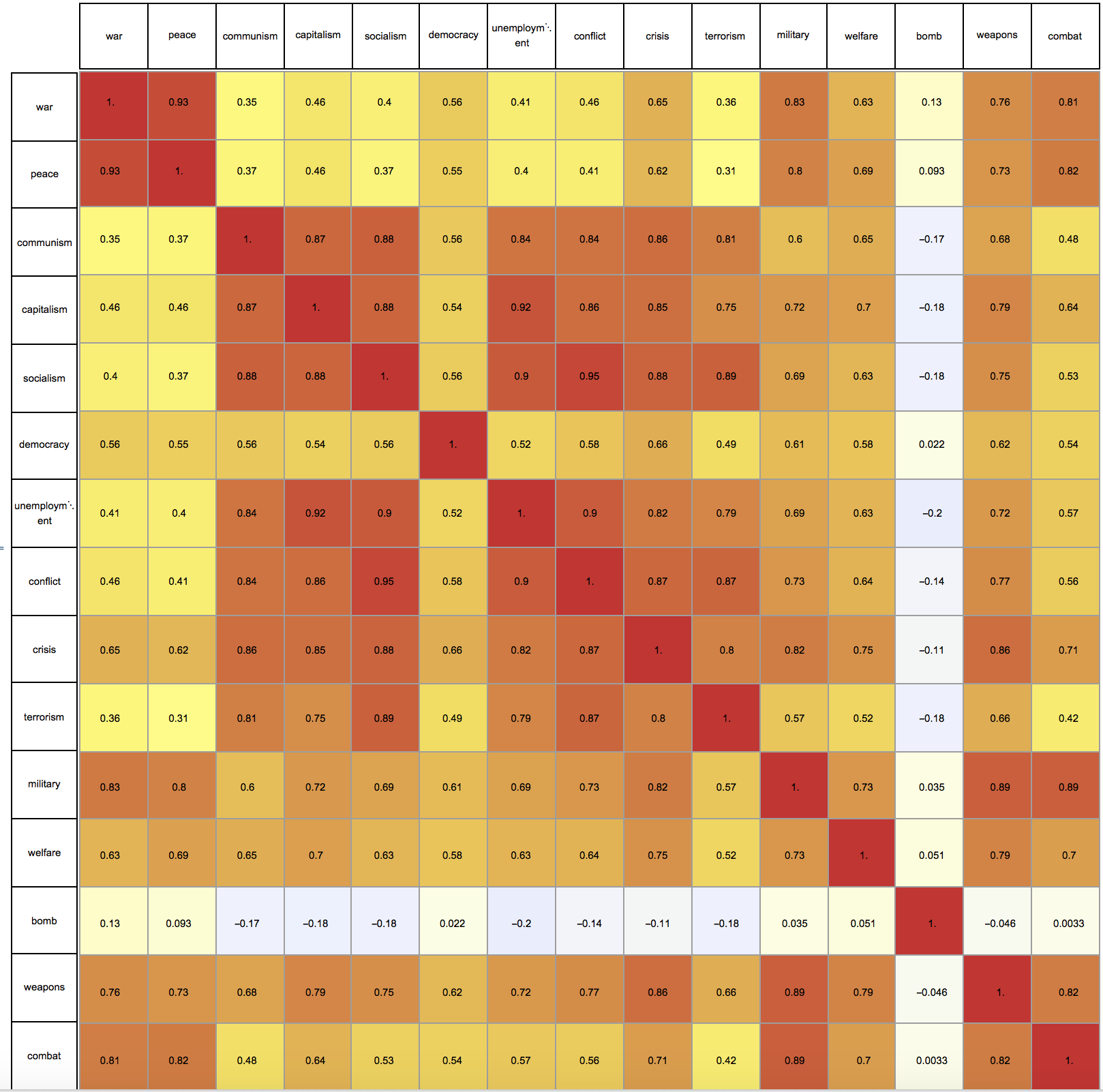
We can use a BandwidthOrdering

Needs["GraphUtilities`"]
{r, c} = MinimumBandwidthOrdering[cm, Method -> "RCMD"]

cm2 = Correlation[
   Transpose@
    worddata[[r]][[All, 
      1 ;; Min[
        Table[Length[worddata[[r]][[i, ;;]]], {i, 1, 
          Length[words]}]]]]];

Column[{GraphicsRow[words[[r]], ImageSize -> 1000, Frame -> All], 
  Row[{GraphicsColumn[words[[r]], ImageSize -> 67, Frame -> All], 
    Overlay[{ArrayPlot[cm2, 
       ColorFunction -> (ColorData["TemperatureMap"][(1 + #)/2] &), 
       Frame -> None, Mesh -> True, PlotRangePadding -> 0, 
       ImageSize -> 1000, ColorFunctionScaling -> False], 
      GraphicsGrid[Map[NumberForm[#, 2] &, cm2, {2}], 
       ImageSize -> 1000]}]}]}, Alignment -> Right, Spacings -> 0]

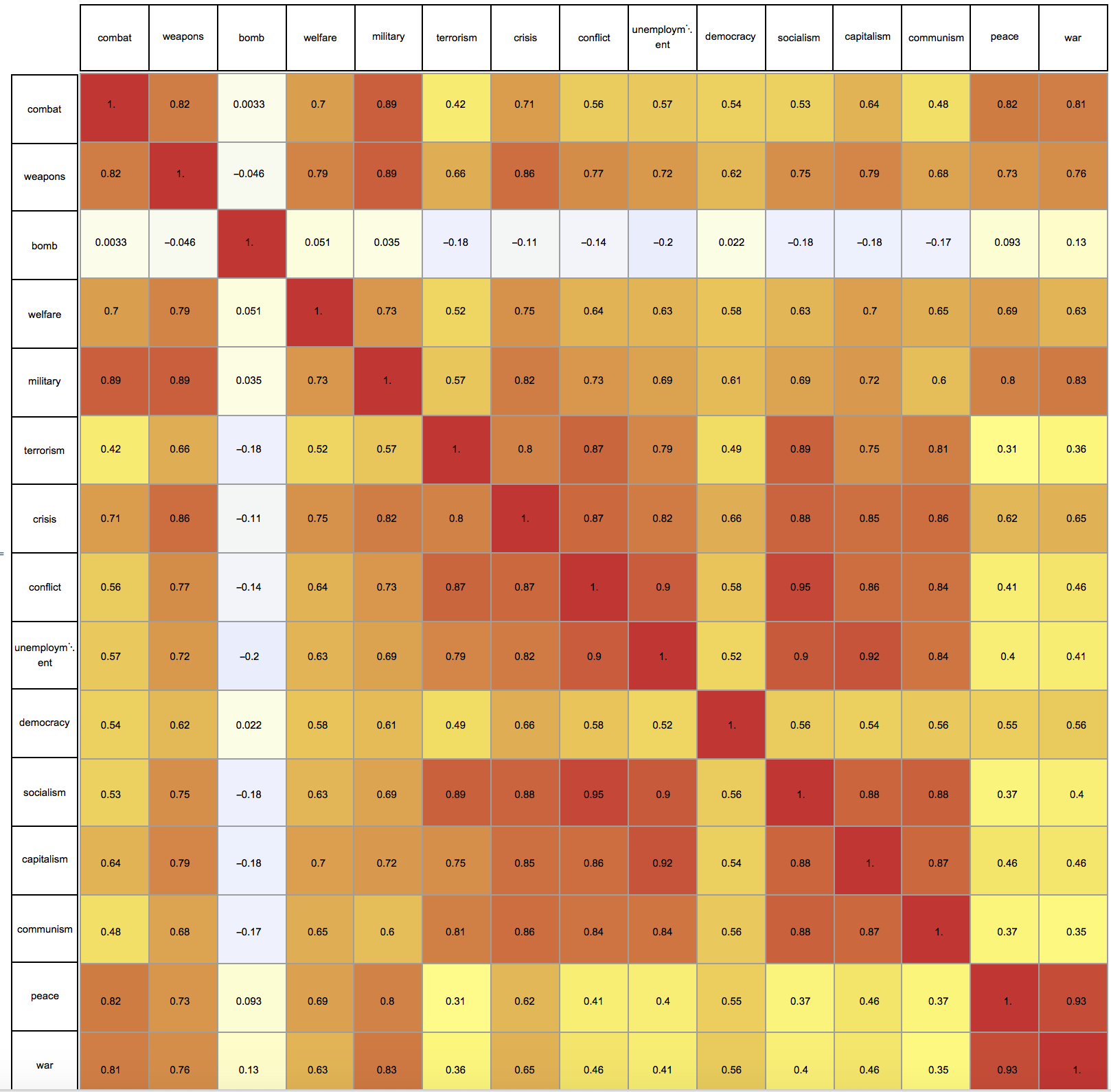
Using that we can try to find words with a similar behaviour:

StackedDateListPlot[
 MapThread[Callout, 
  Log /@ {Values[
     WordFrequencyData[{"Democracy", "War", "Peace"}, 
      "TimeSeries"]], {"Democracy", "War", "Peace"}}], 
 PlotRange -> All, PlotLayout -> "Percentile", ImageSize -> Large, 
 PlotStyle -> {Red, Green, Blue}, LabelStyle -> Directive[Bold, 16], 
 PlotTheme -> "Detailed"]

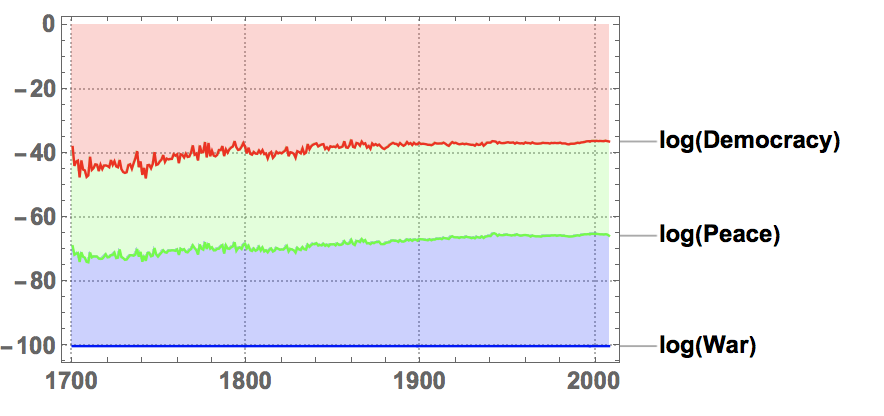
which indicates near constant ratios over a long time. This is not that easy to see in the FrequencyPlot

WordFrequencyPlot[{"Democracy", "War", "Peace"}, "YearStart" -> 1900, 
 "YearEnd" -> Now, "Scaling" -> {None, "Log"}]

.

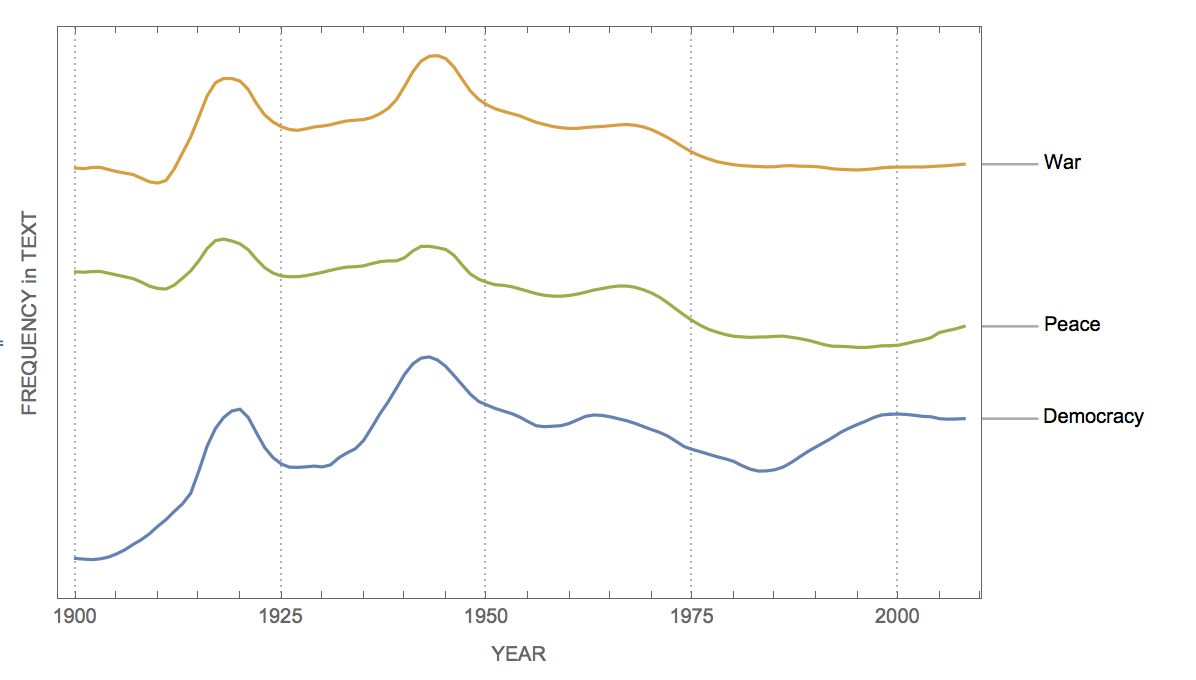Finally, it is interesting to look at other languages such as tu vs usted in Spanish

Options[WordFrequencyPlotSpanish] = {"YearStart" -> 1800, 
"YearEnd" -> Now, "Case" -> True, "Smooth" -> 3, "Scaling" -> None,
"Style" -> Automatic};

WordFrequencyPlotSpanish[words_, OptionsPattern[]] := 
With[{$data = 
WordFrequencyData[words, 
"TimeSeries", {OptionValue["YearStart"], OptionValue["YearEnd"]},
IgnoreCase -> OptionValue["Case"], Language -> "Spanish"]}, 
DateListPlot[
MapThread[
Callout, {MeanFilter[#, 
Quantity[OptionValue["Smooth"], "Years"]] & /@ Values[$data], 
words}], ScalingFunctions -> OptionValue["Scaling"], 
PlotRange -> All, PlotTheme -> "Detailed", 
PlotStyle -> OptionValue["Style"], FrameTicks -> {Automatic, None},
ImageSize -> Large, FrameLabel -> {"YEAR", "FREQUENCY in TEXT"}]]

WordFrequencyPlotSpanish[{"vosotros", "ustedes"}]

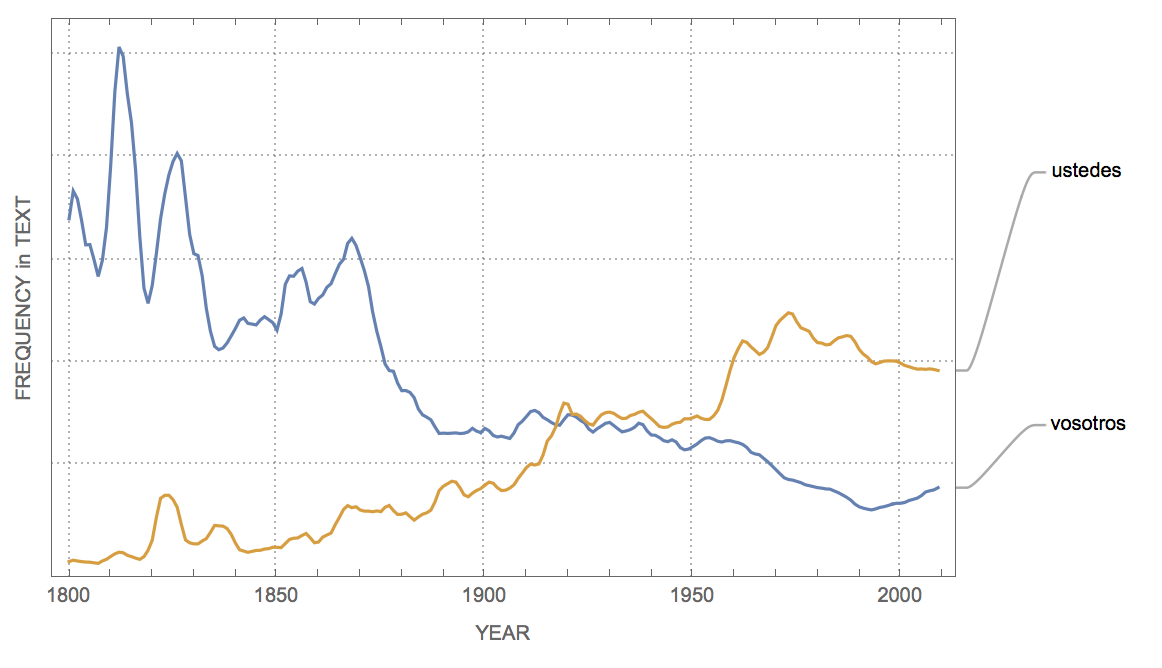
or Du and Sie in German

Options[WordFrequencyPlotGerman] = {"YearStart" -> 1800, 
"YearEnd" -> Now, "Case" -> True, "Smooth" -> 3, "Scaling" -> None,
"Style" -> Automatic};

WordFrequencyPlotGerman[words_, OptionsPattern[]] := 
With[{$data = 
WordFrequencyData[words, 
"TimeSeries", {OptionValue["YearStart"], 
OptionValue["YearEnd"]},(*IgnoreCase\[Rule]OptionValue["Case"],*)
IgnoreCase -> False, Language -> "German"]}, 
DateListPlot[
MapThread[
Callout, {MeanFilter[#, 
Quantity[OptionValue["Smooth"], "Years"]] & /@ Values[$data], 
words}], ScalingFunctions -> OptionValue["Scaling"], 
PlotRange -> All, PlotTheme -> "Detailed", 
PlotStyle -> OptionValue["Style"], FrameTicks -> {Automatic, None},
ImageSize -> Large, FrameLabel -> {"YEAR", "FREQUENCY in TEXT"}]]

WordFrequencyPlotGerman[{"Du", "Sie"}]

I suppose that there are interesting mechanisms working here. It definitely feels that "Du" becomes more prevalent as opposed to the more formal "Sie". But there might be an affect due to (social?) media etc. in the opposite direction.

Here are a couple of pronouns in English:

WordFrequencyPlot[{"you", "thou", "ye", "thee", "thy"}, 
 "YearStart" -> 1200, "YearEnd" -> Now]

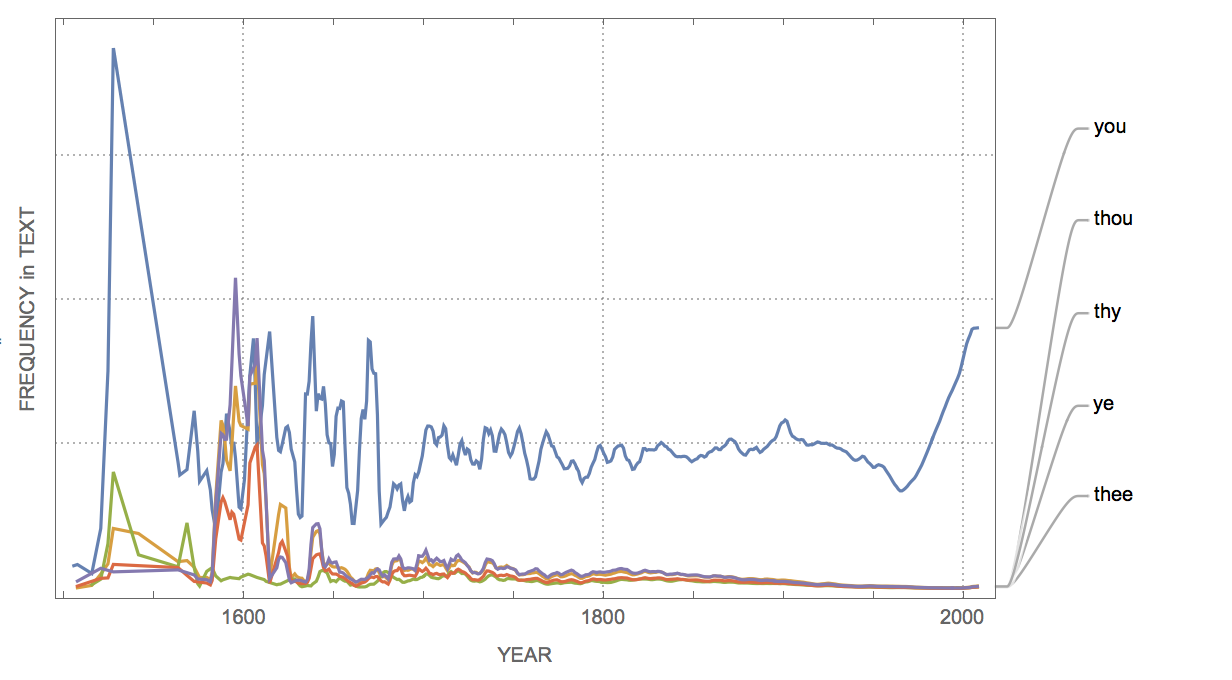
which might look better on a percentile plot:

StackedDateListPlot[
 MapThread[
  Callout, {Values[
    WordFrequencyData[{"you", "thou", "ye", "thee", "thy"}, 
     "TimeSeries"]], {"you", "thou", "ye", "thee", "thy"}}], 
 PlotRange -> All, PlotLayout -> "Percentile", ImageSize -> Large, 
 PlotStyle -> RandomColor[5], LabelStyle -> Directive[Bold, 16], 
 PlotTheme -> "Detailed"]

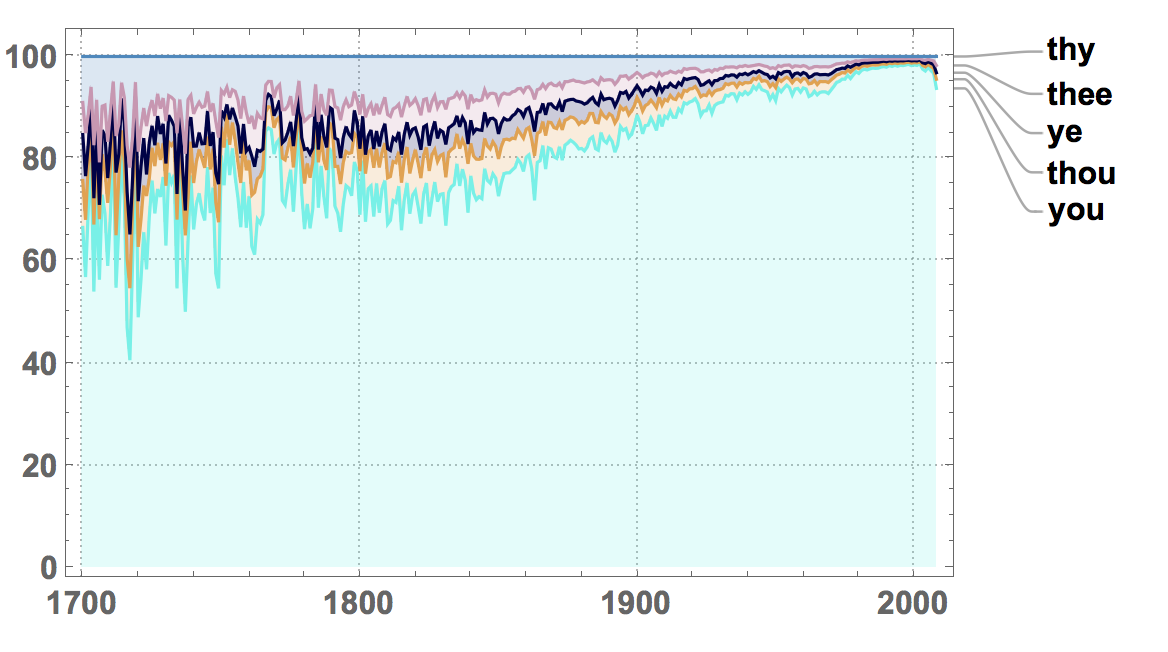
Logarithmically, this becomes:

StackedDateListPlot[
 MapThread[Callout, 
  Log@{Values[
     WordFrequencyData[{"you", "thou", "ye", "thee", "thy"}, 
      "TimeSeries"]], {"you", "thou", "ye", "thee", "thy"}}], 
 PlotRange -> All, PlotLayout -> "Percentile", ImageSize -> Large, 
 PlotStyle -> RandomColor[5], LabelStyle -> Directive[Bold, 16], 
 PlotTheme -> "Detailed"]

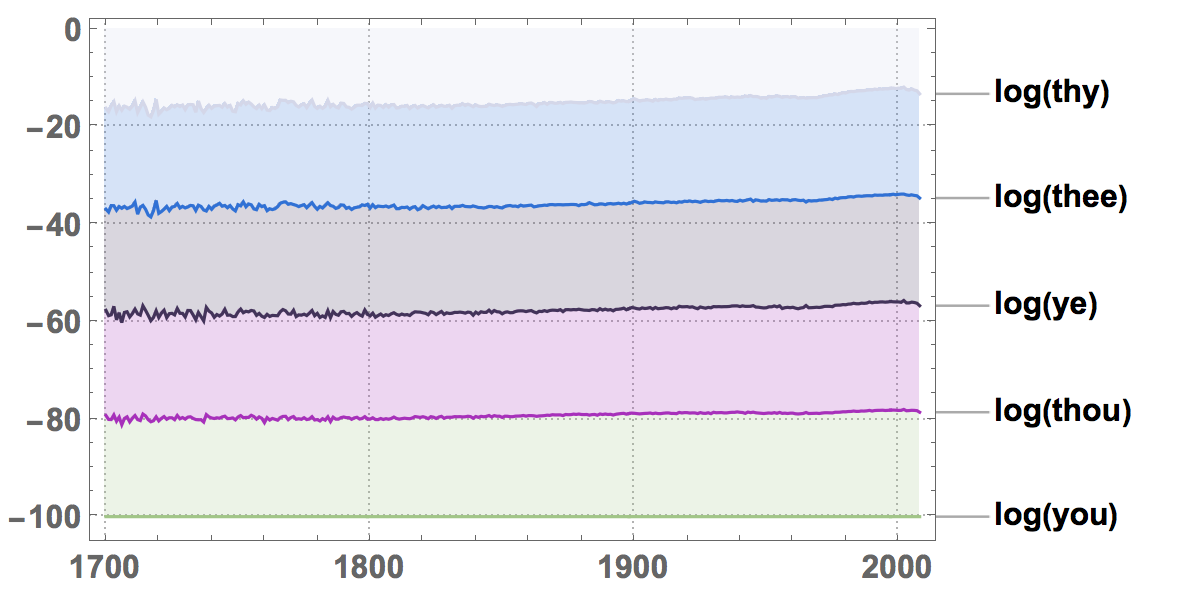
Cheers,

Marco

Curiosity killed the cat:

WordFrequencyPlot[{"curiosity", "cat"}]

The Five Basic Senses

There are five basic senses: touch, sight, hearing, smell and taste. I remember reading somewhere that the maximal information flow human experience normally is due to the vision. The diagram below reflects on that, - note it is a logarithmic scale, - word "see" is much more frequent than others (Although it can have other meanings too, besides the direct act of vision itself, like "understand" etc. But so can other words too.). Note curious fall of "taste" below "hear" and "touch".

WordFrequencyPlot[{"see", "hear", "touch", "taste", "smell"}, "Scaling" -> "Log"]

Trigonometry and Calculator

WordFrequencyPlot[{"trigonometry", "calculator"}]

It's a pretty well-know fact and self-evident that calculators have ruined trigonometry.

Smartphone, iPhone, Apple, Samsung, Orange

WordFrequencyPlot[{"iPhone", "Smartphone", "Samsung", "Apple", 
  "Orange"}, "Scaling" -> "Log"]

People back in 1900 didn't think iPhone was the best phone ever. But if you think Apple is the best company ever, have you ever tried Orange? Way more stable and reliable.

I didn't resist in a humorist take in this thread.

Social Occupation

The King is still the king, unbelievable

may be the King of Rock n'Roll and the King of Pop are included. Without the king

the servant declines, the employee raises, not much gain in it, isn't it? The abolition of slavery seems to be reflected.

World Powers

Freedom, Liberty, Justice, Equality

WordFrequencyPlot[{"freedom", "liberty", "justice", "equality"}]

Political theorists dating back to the Hellenic period have examined the tensions between these concepts, especially between equality and freedom. It's interesting to see how "equality" stays fairly flat while "justice" and "liberty" have decreased (though "justice" seems to be on a relatively recent uptick). Interestingly, "freedom" has increased over time, especially around the time of World War II and the following decades.

Four letter words from f to k

These are more than one and the one does not come up (OMG):

flak was important during WW II - even here it throws its shadows ....

Colors and the "rise" of blue

I think colors are quite interesting. In the plots below note the "rise of blue" in texts. There is a research field that relates language and perception of color. See for example "Russian blues reveal effects of language on color discrimination". Color blue takes a special place, in some opinions less frequent in ancient literature. Also many languages do not distinguish between what in English are described as "blue" and "green" and instead use a cover term spanning both; this might have an effect on English translations. Please respond to this comment if you have any thoughts about this phenomenon.

color={"white","black","red","yellow","green","blue",
            "orange","purple","gray","indigo","pink"};
Interpreter["Color"][color]

Show [WordFrequencyPlot[color[[;; 6]], "Case" -> False, "Scaling" -> "Log", 
"Style" -> Interpreter["Color"][color[[;; 6]]]],Background -> GrayLevel[.8]]

A bit more of colors in regular non-Log scaling:

Show [WordFrequencyPlot[color, "Case" -> False, 
"Style" -> Interpreter["Color"][color]], Background -> GrayLevel[.8]]

Communist political ideologies and systems

https://en.wikipedia.org/wiki/Communism

The raise and peak of communism mentions happens during cold war and existence of Soviet Union (USSR). The emergence of the Soviet Union as the world's first nominally communist state led to communism's widespread association with Marxism–Leninism and the Soviet economic model. Almost all communist governments in the 20th century espoused Marxism–Leninism or a variation of it.

WordFrequencyPlot[{"Leninism", "Marxism", "Stalinism", "Trotskyism"}]

Navigator's tools. Notice the blip during WWII:

WordFrequencyPlot[{"sextant", "chronometer", "compass", "pelorus", 
  "almanac"}, "Scaling" -> "Log"]

Which temple?

The fall of religion to philosophy, the rise of information, data and technology, the drama is evolving ;-) Note the usage of "technology"|"tech" which adds the frequencies of both. Anyone who read "American Gods" by Neil Gaiman might relate.

WordFrequencyPlot[{"science","technology"|"tech","religion","philosophy",
"sense","wisdom","reason","wit","logic","truth","information","data","knowledge"}]

Transportation

WordFrequencyPlot[{"airplane", "car", "train", "speed"}]

- A man who writen "Philosophiæ Naturalis Principia Mathematica".

 WordFrequencyPlot[{"Pythagoras", "Archimedes", "Euclid", "Fibonacci", 
      "Descartes", "Newton", "Leibniz", "Gauss", "Euler", "Fermat", 
      "Turing"}, "YearStart" -> 1800]

WordFrequencyPlot[{"Newton", "Copernicus", "Gauss", "Einstein", 
  "Hawking"}, "YearStart" -> 18

When something is wrong with a human

I was curious to see the vocabulary related to description of issues with human health. Excluded words like "disorder" which have too much wait form non-medical domains.

WordFrequencyPlot[{
"disease","illness","malady","sickness","syndrome","ailment",
"affliction","flu","fever","epidemic","plague","infection"}]

MRB

Here are my initials's (MRB) occurrence since I was born. (I discovered the MRB constant in 1999 -- any connection between that and the MRB uptick in the graph after 2000?)

ClearAll@WordFrequencyPlot;

Options[WordFrequencyPlot] = {"YearStart" -> 1995, "YearEnd" -> Now, 
   "Case" -> True, "Smooth" -> 3, "Scaling" -> None, 
   "Style" -> Automatic};

WordFrequencyPlot[words_, OptionsPattern[]] := 
 With[{$data = 
    WordFrequencyData[words, 
     "TimeSeries", {OptionValue["YearStart"], OptionValue["YearEnd"]},
      IgnoreCase -> OptionValue["Case"]]}, 
  DateListPlot[
   MapThread[
    Callout, {MeanFilter[#, 
        Quantity[OptionValue["Smooth"], "Years"]] & /@ Values[$data], 
     words}], ScalingFunctions -> OptionValue["Scaling"], 
   PlotRange -> All, PlotTheme -> "Detailed", 
   PlotStyle -> OptionValue["Style"], FrameTicks -> {Automatic, None},
    ImageSize -> Large, FrameLabel -> {"YEAR", "FREQUENCY in TEXT"}]]

See https://en.wikipedia.org/wiki/MRB